ファイル:Integer multiplication by FFT.svg

この SVG ファイルのこの PNG プレビューのサイズ: 666 × 580 ピクセル. その他の解像度: 276 × 240 ピクセル | 551 × 480 ピクセル | 882 × 768 ピクセル | 1,176 × 1,024 ピクセル | 2,352 × 2,048 ピクセル。
元のファイル (SVG ファイル、666 × 580 ピクセル、ファイルサイズ: 79キロバイト)
ファイルの履歴
過去の版のファイルを表示するには、その版の日時をクリックしてください。
| 日時 | サムネイル | 寸法 | 利用者 | コメント | |
|---|---|---|---|---|---|
| 現在の版 | 2011年12月17日 (土) 10:37 | 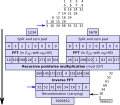 | 666 × 580 (79キロバイト) | Dcoetzee |
ファイルの使用状況
以下の 2 ページがこのファイルを使用しています:
グローバルなファイル使用状況
次に掲げる他のウィキでもこの画像を使用しています:
- de.wikipedia.org での使用状況
- en.wikipedia.org での使用状況
- pl.wikipedia.org での使用状況
- zh.wikipedia.org での使用状況


 French
French Deutsch
Deutsch