有向非巡回グラフ

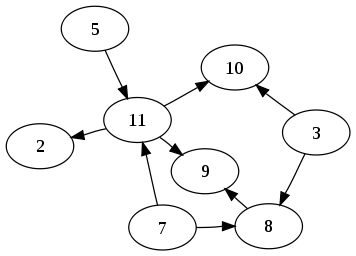
有向非巡回グラフ、有向非循環グラフ、有向無閉路グラフ（ゆうこうひじゅんかいグラフ、英: Directed acyclic graph, DAG）とは、グラフ理論における閉路のない有向グラフのことである。有向グラフは頂点と有向辺（方向を示す矢印付きの辺）からなり、辺は頂点同士をつなぐが、ある頂点 $v$ から出発し、辺をたどり、頂点 $v$ に戻ってこないのが有向非巡回グラフである^[1]^[2]^[3]。

有向非巡回グラフは様々な情報をモデル化するのに使われる。有向非巡回グラフにおける到達可能性は半順序を構成し、全ての有限半順序は到達可能性を利用し有向非巡回グラフで表現可能である。順序づけする必要があるタスクの集合は、あるタスクが他のタスクよりも前に行う必要があるという制約により、頂点をタスク、辺を制約条件で表現すると有向非巡回グラフで表現できる。トポロジカルソートを使うと、妥当な順序を手に入れることができる。加えて、有向非巡回グラフは一部が重なるシーケンスの集合を表現する際の空間効率の良い表現として利用できる。また、有向非巡回グラフはイベント間の因果関係を表現することにも使える。さらに、有向非巡回グラフはデータの流れが一定方向のネットワークを表現することにも使える。

無向グラフにおける対応する概念は森で、森は閉路のない無向グラフである。森から方向を選ぶとpolytreeと呼ばれる特殊な有向非巡回グラフを作ることができる。しかしながら、無向非巡回グラフ（森）に方向付けする方法では作れない有向非巡回グラフがあり、全ての無向グラフはacyclic orientationがあるため、辺に方向付けると有向非巡回グラフになる。この理由から、directed acyclic graphと呼ぶよりもacyclic directed graphと呼ぶ方が正確である。

定義

グラフは、頂点（vertex）と、2 つの頂点を結ぶ辺（edge）によって形成される。頂点は、辺によってペアで接続されるあらゆる種類のオブジェクトである。有向グラフの場合、各辺はある頂点から別の頂点への方向性を持つ。有向グラフの経路（path）とは、各辺の終点となる頂点が次の辺の始点となる頂点と同じであるという性質を持つ辺の列である。経路は、その最初の辺の始点となる頂点が最後の辺の終点となる頂点と同じであるとき、サイクル（閉路）を形成する。有向非巡回グラフは、サイクルを持たない有向グラフのことである^[4]^[5]^[6]。

有向グラフの頂点 $v$ は、頂点 $u$ を始点とし頂点 $v$ を終点とする経路が存在するとき、頂点 $u$ から到達可能であるという。特別な例として、すべての頂点は、自分自身から（辺がの数が 0 の経路によって）到達可能であると考えられる。ある頂点が、非自明な経路（辺の数が 1 つ以上の経路）で自身に到達できる場合、その経路はサイクルである。このため、どの頂点も非自明な経路では自身に到達できないグラフ、としても有向非巡回グラフを定義することができる^[7]。

数学的特性

到達可能性関係・推移閉包・推移簡約

DAG における到達可能性（英語版）関係は、 DAG の頂点の半順序 ≤ として形式化できる。この半順序では、頂点 $u$ と頂点 $v$ は、DAG 内に $u$ から $v$ への有向パスが存在するとき、すなわち $v$ が $u$ から到達可能なときに、 $u$ ≤ $v$ として順序づけられる^[8]。しかし、異なる DAG から、同じ到達可能性関係と同じ半順序集合が得られる場合もある^[9]。例えば、2 つの辺 $a$ → $b$ 、 $b$ → $c$ を持つ DAG は、3 つの辺 $a$ → $b$ 、 $b$ → $c$ 、 $a$ → $c$ を持つ DAG と同じ到達可能性関係を持ち、どちらも頂点が $a$ ≤ $b$ ≤ $c$ の順に並んだ半順序集合を持つ。

有向非巡回グラフ

G

G

の推移簡約

DAG $G$ の推移閉包は、 $G$ と同じ到達可能性関係を表す DAG の中で、最も多くの辺を持つものである。これは、頂点 $u$ から $v$ に到達できるときには必ず辺 $u$ → $v$ を持つ。つまり、 $G$ の到達可能性関係において異なる要素の関連するペア $u$ ≤ $v$ は必ず辺を持つので、到達可能性関係 ≤ をグラフ理論的に直訳したものと考えてよい。この方法はより一般的に有効で、全ての有限半順序集合（ $S$ 、≤）に対して、 $S$ の各メンバーに頂点を持ち、 $u$ ≤ $v$ で関連する要素のペアに辺を持つグラフは、自動的に DAG の推移閉包となり、（ $S$ 、≤）を到達可能性関係として持つ。このようにして、全ての有限半順序集合は、DAG の到達可能性関係として表すことができる。

DAG $G$ の推移簡約（英語版）とは、 $G$ と同じ到達可能性関係を表す DAG の中で、最も少ない辺を持つものである。これは $G$ のサブグラフであり、 $G$ が $u$ から $v$ に至るより長いパスを持つ場合に辺 $u$ → $v$ を廃棄することで形成される。推移閉包と同様、推移簡約も DAG に対して一意に定義される。一方、DAG 以外の有向グラフでは、同じ到達可能性関係を持つ最小部分グラフが複数存在する場合がある^[10]。

DAG $G$ が半順序 ≤ で表される到達可能性関係を持つとき、 $G$ の推移簡約は $G$ サブグラフであり、≤ の被覆関係（英語版）にある全てのペアに対し辺 $u$ → $v$ を持つ。推移簡約は同じ半順序を表す他のグラフに比べて辺の数が少なく、グラフの描画が単純になるため、半順序を視覚化するのに便利である。半順序のハッセ図は、推移簡約を図示したもので、各辺の向きを、辺の始点の頂点を終点の頂点よりも低い位置に置いて示している^[11]。

注釈・出典

^ Christofides, Nicos (1975), Graph theory: an algorithmic approach, Academic Press, pp. 170–174, ISBN 9780121743505 .
^ Thulasiraman, K.; Swamy, M. N. S. (1992), “5.7 Acyclic Directed Graphs”, Graphs: Theory and Algorithms, John Wiley and Son, p. 118, ISBN 978-0-471-51356-8 .
^ Bang-Jensen, Jørgen (2008), “2.1 Acyclic Digraphs”, Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, pp. 32–34, ISBN 978-1-84800-997-4 .
^ Thulasiraman, K.; Swamy, M. N. S. (1992), “5.7 Acyclic Directed Graphs”, Graphs: Theory and Algorithms, John Wiley and Son, p. 118, ISBN 978-0-471-51356-8 .
^ Bang-Jensen, Jørgen (2008), “2.1 Acyclic Digraphs”, Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, pp. 32–34, ISBN 978-1-84800-997-4 .
^ Christofides, Nicos (1975), Graph theory: an algorithmic approach, Academic Press, pp. 170–174
^ Mitrani, I. (1982), Simulation Techniques for Discrete Event Systems, Cambridge Computer Science Texts, 14, Cambridge University Press, p. 27, ISBN 9780521282826
^ Kozen, Dexter (1992), The Design and Analysis of Algorithms, Monographs in Computer Science, Springer, p. 9, ISBN 978-0-387-97687-7
^ Banerjee, Utpal (1993), “Exercise 2(c)”, Loop Transformations for Restructuring Compilers: The Foundations, Springer, p. 19, Bibcode: 1993ltfr.book.....B, ISBN 978-0-7923-9318-4
^ Bang-Jensen, Jørgen; Gutin, Gregory Z. (2008), “2.3 Transitive Digraphs, Transitive Closures and Reductions”, Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics, Springer, pp. 36–39, ISBN 978-1-84800-998-1
^ Jungnickel, Dieter (2012), Graphs, Networks and Algorithms, Algorithms and Computation in Mathematics, 5, Springer, pp. 92–93, ISBN 978-3-642-32278-5 .

外部リンク

Weisstein, Eric W. "Acyclic Digraph". mathworld.wolfram.com (英語).
DAGitty – DAG をつくるためのオンラインツール

この項目は、組合せ数学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています。

[1] Christofides, Nicos (1975), Graph theory: an algorithmic approach, Academic Press, pp. 170–174, ISBN 9780121743505 .

[2] Thulasiraman, K.; Swamy, M. N. S. (1992), “5.7 Acyclic Directed Graphs”, Graphs: Theory and Algorithms, John Wiley and Son, p. 118, ISBN 978-0-471-51356-8 .

[3] Bang-Jensen, Jørgen (2008), “2.1 Acyclic Digraphs”, Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, pp. 32–34, ISBN 978-1-84800-997-4 .

[thul-4] Thulasiraman, K.; Swamy, M. N. S. (1992), “5.7 Acyclic Directed Graphs”, Graphs: Theory and Algorithms, John Wiley and Son, p. 118, ISBN 978-0-471-51356-8 .

[bang-5] Bang-Jensen, Jørgen (2008), “2.1 Acyclic Digraphs”, Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, pp. 32–34, ISBN 978-1-84800-997-4 .

[6] Christofides, Nicos (1975), Graph theory: an algorithmic approach, Academic Press, pp. 170–174

[7] Mitrani, I. (1982), Simulation Techniques for Discrete Event Systems, Cambridge Computer Science Texts, 14, Cambridge University Press, p. 27, ISBN 9780521282826

[8] Kozen, Dexter (1992), The Design and Analysis of Algorithms, Monographs in Computer Science, Springer, p. 9, ISBN 978-0-387-97687-7

[9] Banerjee, Utpal (1993), “Exercise 2(c)”, Loop Transformations for Restructuring Compilers: The Foundations, Springer, p. 19, Bibcode: 1993ltfr.book.....B, ISBN 978-0-7923-9318-4

[10] Bang-Jensen, Jørgen; Gutin, Gregory Z. (2008), “2.3 Transitive Digraphs, Transitive Closures and Reductions”, Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics, Springer, pp. 36–39, ISBN 978-1-84800-998-1

[11] Jungnickel, Dieter (2012), Graphs, Networks and Algorithms, Algorithms and Computation in Mathematics, 5, Springer, pp. 92–93, ISBN 978-3-642-32278-5 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

表話編歴グラフ理論
要素・定義・表現	頂点辺（英語版）グラフ無向有向ラベル付き（英語版）重み付き（英語版）ハイパーグラフ接続行列隣接行列隣接リスト
指標	位数（英語版）サイズ（英語版）次数次数行列距離（英語版）半径直径内周 (頂点)彩色数辺彩色数（英語版）点連結度辺連結度交叉数（英語版）
部分構造	ループ（英語版）多重辺（英語版）部分グラフ（英語版）誘導部分グラフ道閉道連結成分（英語版）強連結成分（英語版）橋（英語版）カットクリーク独立集合支配集合（英語版）マッチングオイラー路シュタイナー木全域木ハミルトン路
全体構造	連結グラフ正則グラフ立方体グラフケージ強正則グラフ木平面グラフ 2部グラフ有向非巡回グラフ弦グラフムーアグラフパーフェクトグラフ対称グラフ半対称グラフ頂点推移グラフ辺推移グラフ距離推移グラフ補グラフ双対グラフグラフ同型
固有名を持つグラフ	パスグラフ（英語版） $P n$ 閉路グラフ $C n$ 完全グラフ $K n$ 完全2部グラフ $K m, n$ スター $S n = K 1, n$ 車輪グラフ $W n$ 空グラフピーターセングラフヒーウッドグラフマギーグラフホフマンシングルトングラフフォークマングラフ
トピック・定理	一筆書きオイラーの多面体定理クラトフスキの定理四色定理五色定理ケイリーの公式プリューファー列最短経路問題巡回セールスマン問題中国人郵便配達問題ダイクストラ法ベルマン-フォード法ワーシャル-フロイド法ハミルトン閉路問題最大クリーク問題頂点被覆問題最小頂点被覆問題最大独立集合問題最大流最小カット定理支配集合問題次数直径問題安定結婚問題
カテゴリ / コモンズ

有向非巡回グラフ

定義

数学的特性

到達可能性関係・推移閉包・推移簡約

注釈・出典

関連項目

外部リンク