点粒子

標準模型
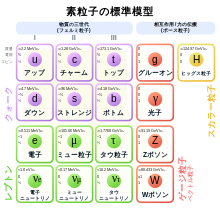標準模型の素粒子

点粒子（英: point particle）は、物理学においてよく用いられる理想化された粒子である。理想粒子 (ideal particle[1]) または点様粒子 (point-like particle, pointlike—) とも言う。

それを定義付ける特徴は空間的広がり（英語版）を持たないことである。ゼロ次元であり空間を占有しない[2]。

概要

[編集]

点粒子は大きさを持たない粒子のことで、空間上のある一点だけに分布する粒子である。通常の物体やそれを構成する原子や分子などは大きさを持ち、点状には分布していないが、ある尺度で点と見なせるような大きさしか持たないなら、それらは点粒子として扱うことができる。このとき、その物体の持つ内部構造などは点粒子の持つ内部自由度として解釈される。たとえばある質量分布を点粒子と見なすなら、その点粒子の質量は分布全体の質量の合計となり、質量の密度は無視される。

大きさを持つ物体を点粒子と見なし得る状況は例えば、物体の大きさに比べて充分長い距離から物体を観測する場合、その形状に関わらず物体は点粒子として振る舞う。この他にも、三次元空間で逆二乗の法則によって記述される相互作用をする球形物体は、その大きさにかかわらず球の外部では、それらの物質が中心に全て集中しているかのように振る舞う。球形物体が外部に作る重力場や電磁場といった場は、球の中心に位置する質量や電荷が等しい点粒子の場と同等であることが知られている[3][4]。

重力などに関係する議論で、質点 (point mass) が用いられることがある。これは質量（マス）がゼロではないというだけの性質を持った点粒子である。同様に電磁気などに関係する議論で、点電荷 (point charge) が用いられることがある。これは電荷（チャージ）がゼロではないというだけの性質を持った点粒子である[5]。他にもそれが必要な場合には、質量と電荷だけを持った点、といったものが用いられることもある。

物体の大きさを決定づけるのは物体同士の相互作用であり、物体そのものは点粒子として記述しつつも、粒子間の相互作用を与えることで物体の大きさを表現することが可能である。

量子力学においては、加えて不確定性原理によって、位置の不確定性から点粒子の「大きさ」を評価できる。例えば、水素原子中の 1s 軌道の電子は、10-30 m3 程度の体積を持つ。ここでいう「大きさ」とは点粒子の存在確率の分布を指し、通常の意味での粒子の大きさではない（点粒子の大きさはゼロである）。

素粒子が点粒子か否かについては議論がある所で、詳細は素粒子の記事を参考のこと。また、量子論的な粒子として、例えば電子を例に挙げると、古典電子半径の他、電子#大きさにあるように、議論の対象によっても扱い方が変わるため、「ある / なし」で単純に決めつけたり、径としてある1つの値を挙げたりできるようなものではない。

質点

[編集]
グリッド上にグラフ化された点粒子の例。灰色の質量は質点（黒い円）に単純化することができる。実際の点は見ることができないので、小円またはドットとして質点を示すことが実用上用いられる。
→詳細は「質点」を参照

質点（しつてん、英: point mass）または点質量（てんしつりょう）は、点様質量（てんようしつりょう、英: pointlike mass）とも呼ばれ、質量のみを持った点である。

応用

[編集]

物理学

[編集]

質点は一般的に重力場の解析に用いられる。系の重力を解析するとき、質量の全単位を個別に計上することは不可能となる。系の中の物体がどれも重心の外周の境界線との重なりを持たないとき、その物体をゼロ次元の質点と見なすことが可能となる。

数学

[編集]

統計学における質点は確率分布における不連続な断片である。そのような質点を計算するには積分が連続区間の確率分布上を確率変数の全定義域に渡って実行される。この積分結果は1に等しくなるように規格化すると、さらなる計算で質点を求めることができる。

点電荷

[編集]
点粒子のスカラーポテンシャルは左から右に動き、すぐに双極子磁石（英語版）を励起する。

点電荷 (point charge) は、電荷を持つ粒子を理想化したモデルであり、電荷をもつが大きさは無い点である。

静電気学の基本方程式はクーロンの法則である。これは二つの点電荷間の電気力を記述する。古典的点電荷と関連する電場は、点電荷からの距離がゼロに近づくにつれ無限に近づき、点電荷のエネルギー（質量）を無限大にする。量子電磁力学において、リチャード・ファインマンらによって開発された繰り込みの数学的手法は点電荷の無限の発散を除去する。

アーンショーの定理は、電荷の静電気学相互作用だけでは点電荷の集合は平衡（英語版）配位において維持することができないことを述べている。

量子力学において

[編集]
陽子は二つのアップクォークと一つのダウンクォークがグルーオンによって結合した複合粒子である。
→詳細は「素粒子」を参照

量子力学において、素粒子と複合粒子は区別される。電子、クォークや光子は素粒子であり内部構造を持たない。一方、陽子や中性子のような複合粒子は素粒子から成る内部構造を持つ粒子である（図を参照）。

素粒子も複合粒子も、不確定性原理のため空間的に局在化しておらず、その波束はいつもゼロではない体積を持つ。例えば、原子軌道では、電子は素粒子だがその量子状態は三次元パターンを形成する。それでも素粒子を点粒子と呼ぶことには意味がある。量子状態に対しては重ね合わせの原理が成り立ち、非局在化した状態の波束を局在化した状態の重ね合わせに分解して表現することができるためである。これは複合粒子を多粒子系として扱う限りにおいては成り立たない。この意味で、物理学者は粒子に固有の内在的な大きさ、すなわち、その波束の「大きさ」ではなくその内部構造の大きさを議論することができ、素粒子の大きさは厳密にゼロである。なお、空間･長さの最小単位の候補としてプランク長があり、素粒子とのプランク長以下の距離を定義可能であるかどうかは明らかではない。

例えば電子について、実験的証拠は電子の「大きさ」は 10-18 m 以下であることを示している[6]。これは厳密なゼロという期待値と矛盾しない（古典電子半径と混同しないこと。これは実際の電子の大きさとは関係しない概念である）。電子には外部と内部を明確に区別をする境界基準が存在しない。上記プランク長スケールより短い距離が存在しない場合には、そのスケール(逆にプランク長より小さな、無限に短い距離が定義可能である場合には素粒子にはシュバルツシルト半径が存在することになる。)で点粒子とみなすには困難を伴うことから、プランク長スケールにおいては有限の大きさを持つ紐として扱う超弦理論も提案されている。

関連項目

[編集]

脚注

[編集]

注釈

[編集]
  1. ^ H.C. Ohanian, J.T. Markert (2007), p. 3
  2. ^ F.E. Udwadia, R.E. Kalaba (2007), p. 1
  3. ^ I. Newton, I.B Cohen, A. Whitmann (1999), p. 956 (Proposition 75, Theorem 35)
  4. ^ I. Newton, A. Motte, J. Machin (1729), p. 270–271
  5. ^ R. Snieder (2001), pp. 196–198
  6. ^ “Precision pins down the electron's magnetism”. 2012年1月10日閲覧。

参考文献

[編集]
  • H.C. Ohanian, J.T. Markert (2007). Physics for Engineers and Scientists. 1 (3rd ed.). Norton. ISBN 9780393930030 
  • F.E. Udwadia, R.E. Kalaba (2007). Analytical Dynamics: A New Approach. Cambridge University Press. ISBN 0521048338 
  • R. Snieder (2001). A Guided Tour of Mathematical Methods for the Physical Sciences. Cambridge University Press. ISBN 0521787513 
  • I. Newton (1729). The Mathematical Principles of Natural Philosophy. A. Motte, J. Machin (trans.). Benjamin Motte. https://books.google.co.jp/books?id=Tm0FAAAAQAAJ&pg=PA270&redir_esc=y&hl=ja 
  • I. Newton (1999). The Principia: Mathematical Principles of Natural Philosophy. I.B. Cohen, A. Whitman (trans.). University of California Press. ISBN 0-520-08817-4 
  • C. Quigg (2009). Particle, Elementary. Grolier Online. 2009年7月4日閲覧。
  • S.L. Glashow (2009). "Quark". Encyclopedia Americana. Grolier Online. 2009年7月4日閲覧。
  • M. Alonso, E.J. Finn (1968). Fundamental University Physics Volume III: Quantum and Statistical Physics. Addison-Wesley. ISBN 0-201-00262-0 

発展文献

[編集]
  • Eric W. Weisstein, "Point Charge".
  • F. H. J. Cornish, "Classical radiation theory and point charges". Proc. Phys. Soc. 86 427-442, 1965. doi:10.1088/0370-1328/86/3/301
  • O. D. Jefimenko, "Direct calculation of the electric and magnetic fields of an electric point charge moving with constant velocity". Am. J. Phys.62 (1994), 79.
「https://ja.wikipedia.org/w/index.php?title=点粒子&oldid=95727727」から取得