数学 において、逆三角関数 (ぎゃくさんかくかんすう、逆三角函数 、英 : inverse trigonometric function 、時折 cyclometric function [ 1] 定義域 を適切に制限した)三角関数 の逆関数 である。具体的には、それらは正弦 (sine) 、余弦 (cosine) 、正接 (tangent) 、余接 (cotangent) 、正割 (secant) 、余割 (cosecant) 関数の逆関数である。これらは三角関数値から角度を得るために使われる。逆三角関数は工学 、航法 、物理学 、幾何学 において広く使われる。
逆三角関数の表記はたくさんある。しばしば sin−1 (x ), cos−1 (x ), tan−1 (x ) sin2 (x ) といった、写像の合成 ではなく冪乗 を意味する表記と混同し、それゆえ合成的逆 と乗法逆元 との混乱を起こす可能性がある。三角関数には各逆数に名称が付されており、(cos x )−1 = sec x [ 2] Sin−1 (x ), Cos−1 (x ) 大文字の (英語版 ) −1 sin−1 (x ), cos−1 (x ) [ 3] −1 の添え字の混乱は完全に解消される。その際の表記は arcsin (x ), arccos (x ), arctan (x ), arccot (x ), arcsec (x ), arccsc (x ) コンピュータ言語 では、逆三角関数の表記は通常 asin, acos, atan が使われている。
接頭辞 "arc" の起源は、弧度法 に由来する。例えば、「余弦が x となる角度」は、単位円 において、「余弦が x となる弧 (arc)」と同義である[ 4]
逆正接函数の数表は実用上の要請から、すでにクラウディオス・プトレマイオス によって作成されていたという[ 5]
6つの三角関数はいずれも単射 でないから、その逆関係は多価関数 である。逆関数を考えるには、変域を制限 する。それゆえ逆関数の値域 はもとの関数の定義域の真の部分集合 である。
例えば、平方根 関数 y = √ x y 2 = x y = arcsin(x )sin(y ) = x sin y = x y は無数にある;例えば 0 = sin 0 = sin π = sin 2π = … 主枝 (英語版 ) x に対して表現 arcsin(x ) はその主値 と呼ばれるただ1つの値だけを返す。これらの性質はすべての逆三角関数について同様に当てはまる。
主逆関数は以下の表にリストされる。
名前 通常の表記 定義 実数を与える x の定義域 通常の主値の終域ラジアン ) 通常の主値の終域度 ) 逆正弦 y = arcsin x x = sin y −1 ≤ x ≤ 1 −π / 2 y ≤ π / 2 −90° ≤ y ≤ 90° 逆余弦 y = arccos x x = cos y −1 ≤ x ≤ 1 0 ≤ y ≤ π 0° ≤ y ≤ 180° 逆正接 y = arctan x x = tan y すべての実数 −π / 2 y < π / 2 −90° < y < 90° 逆余接 y = arccot x x = cot y すべての実数 0 < y < π 0° < y < 180° 逆正割 y = arcsec x x = sec y x ≤ −1 or 1 ≤ x 0 ≤ y < π / 2 π / 2 y ≤ π 0° ≤ y < 90° or 90° < y ≤ 180° 逆余割 y = arccsc x x = csc y x ≤ −1 or 1 ≤ x −π / 2 y < 0 or 0 < y ≤ π / 2 −90° ≤ y < 0° or 0° < y ≤ 90°
(注意:逆正割関数の終域を (0 ≤ y < π / 2 y < 3 / 2 tan(arcsec(x )) = √ x 2 − 1 (0 ≤ y < π / 2 π / 2 y ≤ π) tan(arcsec(x )) = ± √ x 2 − 1 0 ≤ y < π / 2 π / 2 y ≤ π(−π < y ≤ −π / 2 y ≤ π / 2
x が複素数 であることを許す場合、y の終域はその実部にのみ適用する。
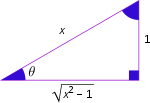
逆三角関数の三角関数を以下の表に示す。表にある関係を導くには、単純には幾何学的な考察から、直角三角形 の一辺の長さを 1 とし、他方の辺の長さを 0 ≤ x ≤ 1 ピタゴラスの定理 と三角比の定義を適用すればよい(表中の図を参照)。このような幾何学的な手段を用いない、純代数学的導出はより長いものとなる。
θ {\displaystyle \theta } sin θ {\displaystyle \sin \theta } cos θ {\displaystyle \cos \theta } tan θ {\displaystyle \tan \theta } 図 arcsin x {\displaystyle \arcsin x} sin arcsin x = x {\displaystyle \sin \arcsin x=x} cos arcsin x = 1 − x 2 {\displaystyle \cos \arcsin x={\sqrt {1-x^{2}}}} tan arcsin x = x 1 − x 2 {\displaystyle \tan \arcsin x={\frac {x}{\sqrt {1-x^{2}}}}} arccos x {\displaystyle \arccos x} sin arccos x = 1 − x 2 {\displaystyle \sin \arccos x={\sqrt {1-x^{2}}}} cos arccos x = x {\displaystyle \cos \arccos x=x} tan arccos x = 1 − x 2 x {\displaystyle \tan \arccos x={\frac {\sqrt {1-x^{2}}}{x}}} arctan x {\displaystyle \arctan x} sin arctan x = x 1 + x 2 {\displaystyle \sin \arctan x={\frac {x}{\sqrt {1+x^{2}}}}} cos arctan x = 1 1 + x 2 {\displaystyle \cos \arctan x={\frac {1}{\sqrt {1+x^{2}}}}} tan arctan x = x {\displaystyle \tan \arctan x=x} arccot x {\displaystyle \operatorname {arccot} x} sin arccot x = 1 1 + x 2 {\displaystyle \sin \operatorname {arccot} x={\frac {1}{\sqrt {1+x^{2}}}}} cos arccot x = x 1 + x 2 {\displaystyle \cos \operatorname {arccot} x={\frac {x}{\sqrt {1+x^{2}}}}} tan arccot x = 1 x {\displaystyle \tan \operatorname {arccot} x={\frac {1}{x}}} arcsec x {\displaystyle \operatorname {arcsec} x} sin arcsec x = x 2 − 1 x {\displaystyle \sin \operatorname {arcsec} x={\frac {\sqrt {x^{2}-1}}{x}}} cos arcsec x = 1 x {\displaystyle \cos \operatorname {arcsec} x={\frac {1}{x}}} tan arcsec x = x 2 − 1 {\displaystyle \tan \operatorname {arcsec} x={\sqrt {x^{2}-1}}} arccsc x {\displaystyle \operatorname {arccsc} x} sin arccsc x = 1 x {\displaystyle \sin \operatorname {arccsc} x={\frac {1}{x}}} cos arccsc x = x 2 − 1 x {\displaystyle \cos \operatorname {arccsc} x={\frac {\sqrt {x^{2}-1}}{x}}} tan arccsc x = 1 x 2 − 1 {\displaystyle \tan \operatorname {arccsc} x={\frac {1}{\sqrt {x^{2}-1}}}}
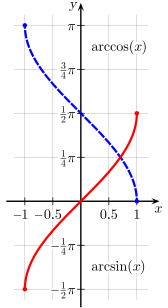
平面上の直交座標系で図示された arcsin(x )(赤 )と arccos(x )(青 )の通常の定義における主値。 平面上の直交座標系で図示された arctan(x )(赤 )と arccot(x )(青 )の通常の定義における主値。 平面上の直交座標系で図示された arcsec(x )(赤 )と arccsc(x )(青 )の主値。 余角:
arccos x = π 2 − arcsin x arccot x = π 2 − arctan x arccsc x = π 2 − arcsec x {\displaystyle {\begin{aligned}\arccos x&={\frac {\pi }{2}}-\arcsin x\\\operatorname {arccot} x&={\frac {\pi }{2}}-\arctan x\\\operatorname {arccsc} x&={\frac {\pi }{2}}-\operatorname {arcsec} x\end{aligned}}} 負角:
arcsin ( − x ) = − arcsin x arccos ( − x ) = π − arccos x arctan ( − x ) = − arctan x arccot ( − x ) = π − arccot x arcsec ( − x ) = π − arcsec x arccsc ( − x ) = − arccsc x {\displaystyle {\begin{aligned}\arcsin(-x)&=-\arcsin x\\\arccos(-x)&=\pi -\arccos x\\\arctan(-x)&=-\arctan x\\\operatorname {arccot}(-x)&=\pi -\operatorname {arccot} x\\\operatorname {arcsec}(-x)&=\pi -\operatorname {arcsec} x\\\operatorname {arccsc}(-x)&=-\operatorname {arccsc} x\end{aligned}}} 逆数:
arccos 1 x = arcsec x arcsin 1 x = arccsc x arctan 1 x = π 2 − arctan x = arccot x , if x > 0 arctan 1 x = − π 2 − arctan x = − π + arccot x , if x < 0 arccot 1 x = π 2 − arccot x = arctan x , if x > 0 arccot 1 x = 3 2 π − arccot x = π + arctan x , if x < 0 arcsec 1 x = arccos x arccsc 1 x = arcsin x {\displaystyle {\begin{aligned}\arccos {\frac {1}{x}}&=\operatorname {arcsec} x\\\arcsin {\frac {1}{x}}&=\operatorname {arccsc} x\\\arctan {\frac {1}{x}}&={\frac {\pi }{2}}-\arctan x=\operatorname {arccot} x,{\text{ if }}x>0\\\arctan {\frac {1}{x}}&=-{\frac {\pi }{2}}-\arctan x=-\pi +\operatorname {arccot} x,{\text{ if }}x<0\\\operatorname {arccot} {\frac {1}{x}}&={\frac {\pi }{2}}-\operatorname {arccot} x=\arctan x,{\text{ if }}x>0\\\operatorname {arccot} {\frac {1}{x}}&={\frac {3}{2}}\pi -\operatorname {arccot} x=\pi +\arctan x,{\text{ if }}x<0\\\operatorname {arcsec} {\frac {1}{x}}&=\arccos x\\\operatorname {arccsc} {\frac {1}{x}}&=\arcsin x\end{aligned}}} 表 から sin の項目を参照すれば:
arccos x = arcsin 1 − x 2 , if 0 ≤ x ≤ 1 arctan x = arcsin x 1 + x 2 {\displaystyle {\begin{aligned}\arccos x&=\arcsin {\sqrt {1-x^{2}}},{\text{ if }}0\leq x\leq 1\\\arctan x&=\arcsin {\frac {x}{\sqrt {1+x^{2}}}}\end{aligned}}} ここでは複素数の平方根を、正の実部(あるいは平方が負の実数であれば正の虚部)を持つように選ぶ。
半角公式 (英語版 ) tan θ 2 = sin θ 1 + cos θ {\displaystyle \tan {\frac {\theta }{2}}={\frac {\sin \theta }{1+\cos \theta }}}
arcsin x = 2 arctan x 1 + 1 − x 2 arccos x = 2 arctan 1 − x 2 1 + x , if − 1 < x ≤ + 1 arctan x = 2 arctan x 1 + 1 + x 2 {\displaystyle {\begin{aligned}\arcsin x&=2\arctan {\frac {x}{1+{\sqrt {1-x^{2}}}}}\\[1ex]\arccos x&=2\arctan {\frac {\sqrt {1-x^{2}}}{1+x}},{\text{ if }}-1<x\leq +1\\[1ex]\arctan x&=2\arctan {\frac {x}{1+{\sqrt {1+x^{2}}}}}\end{aligned}}} arctan u + arctan v = arctan u + v 1 − u v ( mod π ) , u v ≠ 1 . {\displaystyle \arctan u+\arctan v=\arctan {\frac {u+v}{1-uv}}{\pmod {\pi }},\qquad uv\neq 1\,.} これは正接の加法定理
tan ( α + β ) = tan α + tan β 1 − tan α tan β {\displaystyle \tan(\alpha +\beta )={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}} から
α = arctan u , β = arctan v {\displaystyle \alpha =\arctan u\,,\quad \beta =\arctan v} とすることで導かれる。
z の複素数値の導関数 は次の通りである:
d d z arcsin z = 1 1 − z 2 ; z ≠ ± 1 d d z arccos z = − 1 1 − z 2 ; z ≠ ± 1 d d z arctan z = 1 1 + z 2 ; z ≠ ± i d d z arccot z = − 1 1 + z 2 ; z ≠ ± i d d z arcsec z = 1 z 2 1 − z − 2 ; z ≠ 0 , ± 1 d d z arccsc z = − 1 z 2 1 − z − 2 ; z ≠ 0 , ± 1 {\displaystyle {\begin{aligned}{\frac {d}{dz}}\arcsin z&={\frac {1}{\sqrt {1-z^{2}}}};\quad z\neq \pm 1\\{\frac {d}{dz}}\arccos z&={\frac {-1}{\sqrt {1-z^{2}}}};\quad z\neq \pm 1\\{\frac {d}{dz}}\arctan z&={\frac {1}{1+z^{2}}};\quad z\neq \pm i\\{\frac {d}{dz}}\operatorname {arccot} z&={\frac {-1}{1+z^{2}}};\quad z\neq \pm i\\{\frac {d}{dz}}\operatorname {arcsec} z&={\frac {1}{z^{2}{\sqrt {1-z^{-2}}}}};\quad z\neq 0,\pm 1\\{\frac {d}{dz}}\operatorname {arccsc} z&={\frac {-1}{z^{2}{\sqrt {1-z^{-2}}}}};\quad z\neq 0,\pm 1\end{aligned}}} x が実数である場合のみ、以下の関係が成り立つ:
d d x arcsec x = 1 | x | x 2 − 1 ; | x | > 1 d d x arccsc x = − 1 | x | x 2 − 1 ; | x | > 1 {\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arcsec} x&={\frac {1}{|x|\,{\sqrt {x^{2}-1}}}};\qquad |x|>1\\{\frac {d}{dx}}\operatorname {arccsc} x&={\frac {-1}{|x|\,{\sqrt {x^{2}-1}}}};\qquad |x|>1\end{aligned}}} 導出例:θ = arcsin x
d arcsin x d x = d θ d sin θ = d θ cos θ d θ = 1 cos θ = 1 1 − sin 2 θ = 1 1 − x 2 {\displaystyle {\frac {d\arcsin x}{dx}}={\frac {d\theta }{d\sin \theta }}={\frac {d\theta }{\cos \theta \,d\theta }}={\frac {1}{\cos \theta }}={\frac {1}{\sqrt {1-\sin ^{2}\theta }}}={\frac {1}{\sqrt {1-x^{2}}}}} 導関数を積分し一点で値を固定すると逆三角関数の定積分としての表現が得られる:
arcsin x = ∫ 0 x d z 1 − z 2 , | x | ≤ 1 arccos x = ∫ x 1 d z 1 − z 2 , | x | ≤ 1 arctan x = ∫ 0 x d z z 2 + 1 , arccot x = ∫ x ∞ d z z 2 + 1 , arcsec x = ∫ 1 x d z z z 2 − 1 , x ≥ 1 arcsec x = π + ∫ x − 1 d z z z 2 − 1 , x ≤ − 1 arccsc x = ∫ x ∞ d z z z 2 − 1 , x ≥ 1 arccsc x = ∫ − ∞ x d z z z 2 − 1 , x ≤ − 1 {\displaystyle {\begin{aligned}\arcsin x&=\int _{0}^{x}{\frac {dz}{\sqrt {1-z^{2}}}},\qquad |x|\leq 1\\\arccos x&=\int _{x}^{1}{\frac {dz}{\sqrt {1-z^{2}}}},\qquad |x|\leq 1\\\arctan x&=\int _{0}^{x}{\frac {dz}{z^{2}+1}},\\\operatorname {arccot} x&=\int _{x}^{\infty }{\frac {dz}{z^{2}+1}},\\\operatorname {arcsec} x&=\int _{1}^{x}{\frac {dz}{z{\sqrt {z^{2}-1}}}},\qquad x\geq 1\\\operatorname {arcsec} x&=\pi +\int _{x}^{-1}{\frac {dz}{z{\sqrt {z^{2}-1}}}},\qquad x\leq -1\\\operatorname {arccsc} x&=\int _{x}^{\infty }{\frac {dz}{z{\sqrt {z^{2}-1}}}},\qquad x\geq 1\\\operatorname {arccsc} x&=\int _{-\infty }^{x}{\frac {dz}{z{\sqrt {z^{2}-1}}}},\qquad x\leq -1\end{aligned}}} x = 1広義積分 としてきちんと定義されている 。
正弦・余弦関数のように、逆三角関数は次のように級数 を用いて計算できる:
arcsin z = ∑ n = 0 ∞ ( 2 n n ) 4 n ( 2 n + 1 ) z 2 n + 1 = ∑ n = 0 ∞ ( 2 n − 1 ) ! ! ( 2 n ) ! ! z 2 n + 1 2 n + 1 = z + ( 1 2 ) z 3 3 + ( 1 ⋅ 3 2 ⋅ 4 ) z 5 5 + ( 1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6 ) z 7 7 + ⋯ ; | z | ≤ 1 {\displaystyle {\begin{aligned}\arcsin z&=\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {\binom {2n}{n}}{4^{n}(2n+1)}}z^{2n+1}\\&=\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {(2n-1)!!}{(2n)!!}}{\dfrac {z^{2n+1}}{2n+1}}\\&=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\dotsb ;\qquad |z|\leq 1\end{aligned}}}
arccos z = π 2 − arcsin z = π 2 − ∑ n = 0 ∞ ( 2 n n ) 4 n ( 2 n + 1 ) z 2 n + 1 = π 2 − ( z + ( 1 2 ) z 3 3 + ( 1 ⋅ 3 2 ⋅ 4 ) z 5 5 + ⋯ ) ; | z | ≤ 1 {\displaystyle {\begin{aligned}\arccos z&={\frac {\pi }{2}}-\arcsin z\\&={\frac {\pi }{2}}-\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {\binom {2n}{n}}{4^{n}(2n+1)}}z^{2n+1}\\&={\frac {\pi }{2}}-\left(z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\dotsb \right);\quad |z|\leq 1\end{aligned}}}
arctan z = ∑ n = 0 ∞ ( − 1 ) n 2 n + 1 z 2 n + 1 = z − z 3 3 + z 5 5 − z 7 7 + ⋯ ; | z | ≤ 1 , z ≠ ± i {\displaystyle {\begin{aligned}\arctan z&=\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {(-1)^{n}}{2n+1}}z^{2n+1}\\&=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\dotsb ;\quad |z|\leq 1,z\neq \pm i\end{aligned}}}
arccot z = π 2 − arctan z = π 2 − ∑ n = 0 ∞ ( − 1 ) n 2 n + 1 z 2 n + 1 = π 2 − ( z − z 3 3 + z 5 5 − z 7 7 + ⋯ ) ; | z | ≤ 1 , z ≠ ± i {\displaystyle {\begin{aligned}\operatorname {arccot} z&={\dfrac {\pi }{2}}-\arctan z\\&={\frac {\pi }{2}}-\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {(-1)^{n}}{2n+1}}z^{2n+1}\\&={\frac {\pi }{2}}-\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\dotsb \right);\quad |z|\leq 1,z\neq \pm i\end{aligned}}}
arcsec z = arccos 1 z = π 2 − ∑ n = 0 ∞ ( 2 n n ) 4 n ( 2 n + 1 ) z − ( 2 n + 1 ) = π 2 − ( z − 1 + ( 1 2 ) z − 3 3 + ( 1 ⋅ 3 2 ⋅ 4 ) z − 5 5 + ⋯ ) ; | z | ≥ 1 {\displaystyle {\begin{aligned}\operatorname {arcsec} z&=\arccos {\frac {1}{z}}\\&={\frac {\pi }{2}}-\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {\binom {2n}{n}}{4^{n}(2n+1)}}z^{-(2n+1)}\\&={\frac {\pi }{2}}-\left(z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\dotsb \right);\quad |z|\geq 1\end{aligned}}}
arccsc z = arcsin 1 z = ∑ n = 0 ∞ ( 2 n n ) 4 n ( 2 n + 1 ) z − ( 2 n + 1 ) = z − 1 + ( 1 2 ) z − 3 3 + ( 1 ⋅ 3 2 ⋅ 4 ) z − 5 5 + ⋯ ; | z | ≥ 1 {\displaystyle {\begin{aligned}\operatorname {arccsc} z&=\arcsin {\frac {1}{z}}\\&=\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {\binom {2n}{n}}{4^{n}(2n+1)}}z^{-(2n+1)}\\&=z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\dotsb ;\quad |z|\geq 1\end{aligned}}} レオンハルト・オイラー (Leonhard Euler ) は逆正接関数のより効率的な級数を見つけた:
arctan z = z 1 + z 2 ∑ n = 0 ∞ ∏ k = 1 n 2 k z 2 ( 2 k + 1 ) ( 1 + z 2 ) . {\displaystyle \arctan z={\frac {z}{1+z^{2}}}\textstyle \sum \limits _{n=0}^{\infty }\prod \limits _{k=1}^{n}{\dfrac {2kz^{2}}{(2k+1)(1+z^{2})}}.} (n = 01 である 0 項の積 であることに注意する。) [ 6]
arctan z = ∑ n = 0 ∞ 2 2 n ( n ! ) 2 ( 2 n + 1 ) ! z 2 n + 1 ( 1 + z 2 ) n + 1 {\displaystyle \arctan z=\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {2^{2n}(n!)^{2}}{(2n+1)!}}\;{\dfrac {z^{\,2n+1}}{(1+z^{2})^{n+1}}}}
( arcsin z ) 2 = ∑ n = 0 ∞ 2 2 n + 1 ( n ! ) 2 ( 2 n + 2 ) ! z 2 n + 2 {\displaystyle (\arcsin z)^{2}=\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {2^{2n+1}(n!)^{2}}{(2n+2)!}}\;z^{\,2n+2}} 逆正接関数の冪級数の2つの代わりはこれらの一般化連分数 (英語版 )
arctan z = z 1 + ( 1 z ) 2 3 − 1 z 2 + ( 3 z ) 2 5 − 3 z 2 + ( 5 z ) 2 7 − 5 z 2 + ( 7 z ) 2 9 − 7 z 2 + ⋱ = z 1 + ( 1 z ) 2 3 + ( 2 z ) 2 5 + ( 3 z ) 2 7 + ( 4 z ) 2 9 + ⋱ {\displaystyle {\begin{aligned}\arctan z&={\cfrac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}\\&={\cfrac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots \,}}}}}}}}}}\end{aligned}}} これらの2番目は cut 複素平面において有効である。−i i から虚軸を上がって無限の点までの2つの cut がある。それは −1 から 1 まで走る実数に対して最もよく働く。部分分母は奇数であり部分分子は(最初の後)単に (nz )2 レオンハルト・オイラー によって開発された。2つ目はガウスの超幾何級数 (英語版 ) カール・フリードリヒ・ガウス (Carl Friedrich Gauss ) によって開発された。
実および複素値 x に対して:
∫ arcsin x d x = x arcsin x + 1 − x 2 + C ∫ arccos x d x = x arccos x − 1 − x 2 + C ∫ arctan x d x = x arctan x − 1 2 log ( 1 + x 2 ) + C ∫ arccot x d x = x arccot x + 1 2 log ( 1 + x 2 ) + C ∫ arcsec x d x = x arcsec x − log [ x ( 1 + x 2 − 1 x 2 ) ] + C ∫ arccsc x d x = x arccsc x + log [ x ( 1 + x 2 − 1 x 2 ) ] + C {\displaystyle {\begin{aligned}\int \arcsin x\,dx&=x\arcsin x+{\sqrt {1-x^{2}}}+C\\\int \arccos x\,dx&=x\arccos x-{\sqrt {1-x^{2}}}+C\\\int \arctan x\,dx&=x\arctan x-{\frac {1}{2}}\log \left(1+x^{2}\right)+C\\\int \operatorname {arccot} x\,dx&=x\operatorname {arccot} x+{\frac {1}{2}}\log \left(1+x^{2}\right)+C\\\int \operatorname {arcsec} x\,dx&=x\operatorname {arcsec} x-\log \left[x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\right)\right]+C\\\int \operatorname {arccsc} x\,dx&=x\operatorname {arccsc} x+\log \left[x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\right)\right]+C\end{aligned}}} 実数 x ≥ 1
∫ arcsec x d x = x arcsec x − log ( x + x 2 − 1 ) + C ∫ arccsc x d x = x arccsc x + log ( x + x 2 − 1 ) + C {\displaystyle {\begin{aligned}\int \operatorname {arcsec} x\,dx&=x\operatorname {arcsec} x-\log \left(x+{\sqrt {x^{2}-1}}\right)+C\\\int \operatorname {arccsc} x\,dx&=x\operatorname {arccsc} x+\log \left(x+{\sqrt {x^{2}-1}}\right)+C\end{aligned}}} これらはすべて部分積分 と上で示された単純な導関数の形 を用いて導出できる。
∫ u d v = u v − ∫ v d u {\displaystyle \int u\,\mathrm {d} v=uv-\int v\,\mathrm {d} u}
u = arcsin x d v = d x d u = d x 1 − x 2 v = x {\displaystyle {\begin{aligned}u&=&\arcsin x&\quad \quad \mathrm {d} v=\mathrm {d} x\\\mathrm {d} u&=&{\frac {\mathrm {d} x}{\sqrt {1-x^{2}}}}&\quad \quad v=x\end{aligned}}} とおく。すると
∫ arcsin x d x = x arcsin x − ∫ x 1 − x 2 d x {\displaystyle \int \arcsin x\,\mathrm {d} x=x\arcsin x-\int {\frac {x}{\sqrt {1-x^{2}}}}\,\mathrm {d} x} k = 1 − x 2 {\displaystyle k=1-x^{2}} と置換 する。すると
d k = − 2 x d x {\displaystyle \mathrm {d} k=-2x\,\mathrm {d} x} そして
∫ x 1 − x 2 d x = − 1 2 ∫ d k k = − k {\displaystyle \int {\frac {x}{\sqrt {1-x^{2}}}}\,\mathrm {d} x=-{\frac {1}{2}}\int {\frac {\mathrm {d} k}{\sqrt {k}}}=-{\sqrt {k}}} x に逆置換すると
∫ arcsin x d x = x arcsin x + 1 − x 2 + C {\displaystyle \int \arcsin x\,\mathrm {d} x=x\arcsin x+{\sqrt {1-x^{2}}}+C} が出る。
逆三角関数は解析関数 であるから、実数直線から複素平面に拡張することができる。その結果は複数のシートと分岐点 を持つ関数になる。拡張を定義する1つの可能な方法は:
arctan z = ∫ 0 z d x 1 + x 2 z ≠ ± i {\displaystyle \arctan z=\int _{0}^{z}{\frac {dx}{1+x^{2}}}\quad z\neq \pm i} ただし −i と +i の真の間にない虚軸の部分は主シートと他のシートの間の cut である;
arcsin z = arctan z 1 − z 2 z ≠ ± 1 {\displaystyle \arcsin z=\arctan {\frac {z}{\sqrt {1-z^{2}}}}\quad z\neq \pm 1} ただし(平方根関数は負の実軸に沿って cut を持ち)−1 と +1 の真の間にない実軸の部分は arcsin の主シートと他のシートの間の cut である;
arccos z = π 2 − arcsin z z ≠ ± 1 {\displaystyle \arccos z={\frac {\pi }{2}}-\arcsin z\quad z\neq \pm 1} これは arcsin と同じ cut を持つ;
arccot z = π 2 − arctan z z ≠ ± i {\displaystyle \operatorname {arccot} z={\frac {\pi }{2}}-\arctan z\quad z\neq \pm i} これは arctan と同じ cut を持つ;
arcsec z = arccos 1 z z ≠ 0 , ± 1 {\displaystyle \operatorname {arcsec} z=\arccos {\frac {1}{z}}\quad z\neq 0,\pm 1} ただし −1 と +1 の両端を含む間の実軸の部分は arcsec の主シートと他のシートの間の cut である;
arccsc z = arcsin 1 z z ≠ 0 , ± 1 {\displaystyle \operatorname {arccsc} z=\arcsin {\frac {1}{z}}\quad z\neq 0,\pm 1} これは arcsec と同じ cut を持つ。
これらの関数は複素対数関数 を使って表現することもできる。これらの関数の対数表現は三角関数の指数関数による表示を経由して初等的な証明が与えられ、その定義域 を複素平面 に自然に拡張する。
arcsin x = − i log ( i x + 1 − x 2 ) = arccsc 1 x arccos x = − i log ( x − i 1 − x 2 ) = π 2 + i log ( i x + 1 − x 2 ) = π 2 − arcsin x = arcsec 1 x arctan x = 1 2 i { log ( 1 − i x ) − log ( 1 + i x ) } = arccot 1 x arccot x = 1 2 i { log ( 1 − i x ) − log ( 1 + i x ) } = arctan 1 x arcsec x = − i log ( i 1 − 1 x 2 + 1 x ) = i log ( 1 − 1 x 2 + i x ) + π 2 = π 2 − arccsc x = arccos 1 x arccsc x = − i log ( 1 − 1 x 2 + i x ) = arcsin 1 x {\displaystyle {\begin{aligned}\arcsin x&=-i\log(ix+{\sqrt {1-x^{2}}})&=\operatorname {arccsc} {\frac {1}{x}}\\[10pt]\arccos x&=-i\log(x-i{\sqrt {1-x^{2}}})={\frac {\pi }{2}}+i\log(ix+{\sqrt {1-x^{2}}})={\frac {\pi }{2}}-\arcsin x&=\operatorname {arcsec} {\frac {1}{x}}\\[10pt]\arctan x&={\frac {1}{2}}i\{\log(1-ix)-\log(1+ix)\}&=\operatorname {arccot} {\frac {1}{x}}\\[10pt]\operatorname {arccot} x&={\frac {1}{2}}i\left\{\log \left(1-{\frac {i}{x}}\right)-\log \left(1+{\frac {i}{x}}\right)\right\}&=\arctan {\frac {1}{x}}\\[10pt]\operatorname {arcsec} x&=-i\log \left(i{\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {1}{x}}\right)=i\log \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)+{\frac {\pi }{2}}={\frac {\pi }{2}}-\operatorname {arccsc} x&=\arccos {\frac {1}{x}}\\[10pt]\operatorname {arccsc} x&=-i\log \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)&=\arcsin {\frac {1}{x}}\end{aligned}}} ここで注意しておきたいことは、複素対数関数における主値は、複素数の偏角部分 arg の主値の取り方に依存して決まることである。それ故に、ここで示した対数表現における主値は、複素対数関数の主値を基準にすると、逆三角関数の主値 で述べた通常の主値と一致しない場合があることに注意する必要がある。一致させたい場合は、対数部の位相をずらすことで対応できる。もし文献により異なる対数表現が与えられているような場合には、主値の範囲を異なる範囲で取る場合であると考えられるので、目的に応じて対数部の位相をずらす必要がある。
arcsin x = θ {\displaystyle \arcsin x=\theta } とおくと、
sin θ = x {\displaystyle \sin \theta =x} 正弦の指数関数による定義 より
e i θ − e − i θ 2 i = x {\displaystyle {\frac {e^{i\theta }-e^{-i\theta }}{2i}}=x} を得る。
k = e i θ {\displaystyle k=e^{i\,\theta }} とおくと
k − 1 k 2 i = x {\displaystyle {\frac {k-{\frac {1}{k}}}{2i}}=x} これを k について解くと、
k 2 − 2 i x k − 1 = 0 {\displaystyle k^{2}-2ix\,k-1=0} e i θ = k = i x ± 1 − x 2 {\displaystyle e^{i\theta }=k=ix\pm {\sqrt {1-x^{2}}}} arcsin x = θ = − i log ( i x ± 1 − x 2 ) {\displaystyle \arcsin x=\theta =-i\log(ix\pm {\sqrt {1-x^{2}}})} (正の分枝を選ぶ) θ = arcsin x {\displaystyle \theta =\arcsin x} e i θ = cos θ + i sin θ {\displaystyle e^{i\theta }=\cos \theta +i\sin \theta } 自然対数を取り、−i を掛け、arcsin x θ に代入する。 arcsin x = − i log ( cos arcsin x + i sin arcsin x ) {\displaystyle \arcsin x=-i\log(\cos \arcsin x+i\sin \arcsin x)} arcsin x = − i log ( 1 − x 2 + i x ) {\displaystyle \arcsin x=-i\log({\sqrt {1-x^{2}}}+ix)} 複素平面 における逆三角関数 arcsin z {\displaystyle \arcsin z} arccos z {\displaystyle \arccos z} arctan z {\displaystyle \arctan z} arccot z {\displaystyle \operatorname {arccot} z} arcsec z {\displaystyle \operatorname {arcsec} z} arccsc z {\displaystyle \operatorname {arccsc} z} 各三角関数は引数の実部において周期的であり、2π の各区間において2度すべてのその値を取る。正弦と余弦は(k を整数として)周期を 2π k − π / 2 π k + π / 2 π k + π / 2 π k + 3 / 2 π までは逆にする。コサインとセカントは周期を 2π k で始め 2π k + π で終わらせそれから 2π k + π から 2π k + 2π まで逆にする。タンジェントは周期を 2π k − π / 2 π k + π / 2 π k + π / 2 π k + 3 / 2 π まで(前へ)繰り返す。コタンジェントは周期を 2π k で始め 2π k + π で終わらせそれから 2π k + π から 2π k + 2π まで(前へ)繰り返す。
この周期性は k を何か整数として一般の逆において反映される:
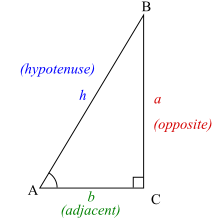
sin y = x ⇔ y = arcsin x + 2 k π or y = π − arcsin x + 2 k π {\displaystyle \sin y=x\ \Leftrightarrow \ y=\arcsin x+2k\pi {\text{ or }}y=\pi -\arcsin x+2k\pi } 1つの方程式に書けば: sin y = x ⇔ y = ( − 1 ) k arcsin x + k π {\displaystyle \sin y=x\ \Leftrightarrow \ y=(-1)^{k}\arcsin x+k\pi } cos y = x ⇔ y = arccos x + 2 k π or y = 2 π − arccos x + 2 k π {\displaystyle \cos y=x\ \Leftrightarrow \ y=\arccos x+2k\pi {\text{ or }}y=2\pi -\arccos x+2k\pi } 1つの方程式に書けば: cos y = x ⇔ y = ± arccos x + 2 k π {\displaystyle \cos y=x\ \Leftrightarrow \ y=\pm \arccos x+2k\pi } tan y = x ⇔ y = arctan x + k π {\displaystyle \tan y=x\ \Leftrightarrow \ y=\arctan x+k\pi } cot y = x ⇔ y = arccot x + k π {\displaystyle \cot y=x\ \Leftrightarrow \ y=\operatorname {arccot} x+k\pi } sec y = x ⇔ y = arcsec x + 2 k π or y = 2 π − arcsec x + 2 k π {\displaystyle \sec y=x\ \Leftrightarrow \ y=\operatorname {arcsec} x+2k\pi {\text{ or }}y=2\pi -\operatorname {arcsec} x+2k\pi } csc y = x ⇔ y = arccsc x + 2 k π or y = π − arccsc x + 2 k π {\displaystyle \csc y=x\ \Leftrightarrow \ y=\operatorname {arccsc} x+2k\pi {\text{ or }}y=\pi -\operatorname {arccsc} x+2k\pi } 直角三角形 逆三角関数は、直角三角形 において、辺の長さから鋭角を求めるときに有用である。例えば sin の直角三角形による定義を思い出すと
θ = arcsin opposite hypotenuse {\displaystyle \theta =\arcsin {\frac {\text{opposite}}{\text{hypotenuse}}}} が従う。しばしば、斜辺 (hypotenuse ) は未知であり arcsin や arccos を使う前に、ピタゴラスの定理 :a 2 + b 2 = h 2 h は斜辺の長さ)を使って計算される必要がある。逆正接関数はこの状況で重宝する、なぜなら斜辺の長さは必要ないからだ。
θ = arctan opposite adjacent . {\displaystyle \theta =\arctan {\frac {\text{opposite}}{\text{adjacent}}}.} 例えば、7 メートル行くと 3 メートル下がる屋根を考えよう。この屋根は水平線と角度 θ をなす。このとき θ は次のように計算できる:
θ = arctan opposite adjacent = arctan rise run = arctan 3 7 ≈ 23.2 ∘ . {\displaystyle \theta =\arctan {\frac {\text{opposite}}{\text{adjacent}}}=\arctan {\frac {\text{rise}}{\text{run}}}=\arctan {\frac {3}{7}}\approx 23.2^{\circ }.} atan2 関数は 2つの引数を取り、与えられた y , x y / x (−π, π] atan2(y , x ) x 軸の正の部分と点 (x , y ) 反時計回り の角度(上半平面、y > 0y < 0atan2 関数は最初多くのコンピュータ言語 に導入されたが、今日では他の科学 や工学 の分野においても一般的に用いられている。なお、マイクロフトのExcel では引数の順番が逆になっている。
atan2 は標準的な arctan 、すなわち終域を (−π / 2 π / 2
atan2 ( y , x ) = { arctan y x x > 0 arctan y x + π y ≥ 0 , x < 0 arctan y x − π y < 0 , x < 0 π 2 y > 0 , x = 0 − π 2 y < 0 , x = 0 u n d e f i n e d y = 0 , x = 0 {\displaystyle \operatorname {atan2} (y,x)={\begin{cases}\arctan {\dfrac {y}{x}}&\qquad x>0\\\arctan {\dfrac {y}{x}}+\pi &\qquad y\geq 0,x<0\\\arctan {\dfrac {y}{x}}-\pi &\qquad y<0,x<0\\{\dfrac {\pi }{2}}&\qquad y>0,x=0\\-{\dfrac {\pi }{2}}&\qquad y<0,x=0\\\mathrm {undefined} &\qquad y=0,x=0\end{cases}}} それはまた複素数 x + iy 偏角 の主値 にも等しい。
この関数はタンジェント半角公式 (英語版 ) x > 0y ≠ 0
atan2 ( y , x ) = 2 arctan y x 2 + y 2 + x {\displaystyle \operatorname {atan2} (y,x)=2\arctan {\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}} しかしながらこれは x ≤ 0y = 0
上の引数の順序 (y , x ) C言語 のようなISO規格 において用いられるが、少数の著者は逆の慣習 (x , y ) atan2 に詳しい。
x, y 共に 0 の場合、インテルの CPU の FPATAN 命令、Javaプラットフォーム 、.NET Framework などは下記ルールに従っている。
atan2(+0, +0) = +0 atan2(+0, −0) = +π atan2(−0, +0) = −0 atan2(−0, −0) = −π 多くの応用において[どれ? 方程式 x = tan y y は与えられた値 −∞ < η < ∞
y = arctan η x := arctan x + π ⋅ rni η − arctan x π {\displaystyle y=\arctan _{\eta }x:=\arctan x+\pi \cdot \operatorname {rni} {\frac {\eta -\arctan x}{\pi }}} によって得られる。丸め関数 rni {\displaystyle \operatorname {rni} } (r ound to the n earest i nteger) 。
0 と π の近くの角度に対して、逆余弦は条件数 であり、計算機において角度計算の実装に用いると精度が落ちてしまう(桁数の制限のため)。同様に、逆正弦は ±π / 2 の近くで精度が低い。すべての角度に対して十分な精度を達成するには、実装では逆正接あるいは atan2 を使うべきである。
arctan はコーシー分布 の、arcsinは逆正弦分布 (英語版 ) 累積分布関数 である。
^ 例えば Dörrie, Heinrich (1965). Triumph der Mathematik . Trans. David Antin. Dover. p. 69. ISBN 0-486-61348-8 ^ Prof. Sanaullah Bhatti; Ch. Nawab-ud-Din; Ch. Bashir Ahmed; Dr. S. M. Yousuf; Dr. Allah Bukhsh Taheem (1999). “Differentiation of Tigonometric, Logarithmic and Exponential Functions”. In Prof. Mohammad Maqbool Ellahi, Dr. Karamat Hussain Dar, Faheem Hussain (Pakistani English). Calculus and Analytic Geometry (First ed.). Lahore : Punjab Textbook Board. p. 140 ^ “逆三角関数―その多価関数性と主値 ”. 岡本良治. 2022年4月1日 閲覧。 ^ "Inverse trigonometric functions" in The Americana: a universal reference library , Vol.21, Ed. Frederick Converse Beach, George Edwin Rines, (1912). ^ 一松信 『教室に電卓を! 3』海鳴社 、1986年11月。^ Chien-Lih, Hwang (2005). “89.67 An Elementary Derivation of Euler's Series for the Arctangent Function” . The Mathematical Gazette 89 (516): 469-470. ISSN 0025-5572 . https://www.jstor.org/stable/3621947 . 








 French
French Deutsch
Deutsch
































![{\displaystyle {\begin{aligned}\arcsin x&=2\arctan {\frac {x}{1+{\sqrt {1-x^{2}}}}}\\[1ex]\arccos x&=2\arctan {\frac {\sqrt {1-x^{2}}}{1+x}},{\text{ if }}-1<x\leq +1\\[1ex]\arctan x&=2\arctan {\frac {x}{1+{\sqrt {1+x^{2}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3301b6cf4f7004e89a5b9eb543769cbf800456e6)

















![{\displaystyle {\begin{aligned}\int \arcsin x\,dx&=x\arcsin x+{\sqrt {1-x^{2}}}+C\\\int \arccos x\,dx&=x\arccos x-{\sqrt {1-x^{2}}}+C\\\int \arctan x\,dx&=x\arctan x-{\frac {1}{2}}\log \left(1+x^{2}\right)+C\\\int \operatorname {arccot} x\,dx&=x\operatorname {arccot} x+{\frac {1}{2}}\log \left(1+x^{2}\right)+C\\\int \operatorname {arcsec} x\,dx&=x\operatorname {arcsec} x-\log \left[x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\right)\right]+C\\\int \operatorname {arccsc} x\,dx&=x\operatorname {arccsc} x+\log \left[x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\right)\right]+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b191070cce0f888e1974de90f44d5f7f35c09368)














![{\displaystyle {\begin{aligned}\arcsin x&=-i\log(ix+{\sqrt {1-x^{2}}})&=\operatorname {arccsc} {\frac {1}{x}}\\[10pt]\arccos x&=-i\log(x-i{\sqrt {1-x^{2}}})={\frac {\pi }{2}}+i\log(ix+{\sqrt {1-x^{2}}})={\frac {\pi }{2}}-\arcsin x&=\operatorname {arcsec} {\frac {1}{x}}\\[10pt]\arctan x&={\frac {1}{2}}i\{\log(1-ix)-\log(1+ix)\}&=\operatorname {arccot} {\frac {1}{x}}\\[10pt]\operatorname {arccot} x&={\frac {1}{2}}i\left\{\log \left(1-{\frac {i}{x}}\right)-\log \left(1+{\frac {i}{x}}\right)\right\}&=\arctan {\frac {1}{x}}\\[10pt]\operatorname {arcsec} x&=-i\log \left(i{\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {1}{x}}\right)=i\log \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)+{\frac {\pi }{2}}={\frac {\pi }{2}}-\operatorname {arccsc} x&=\arccos {\frac {1}{x}}\\[10pt]\operatorname {arccsc} x&=-i\log \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)&=\arcsin {\frac {1}{x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc68ac41d98d258aa0b0adf4d28f9b32bfb4a4a)