錯視
錯視は視覚刺激がその客観的性質と異なるかたちで認識された知覚である。俗に「目の錯覚」ともよばれる。生理的錯覚に属するもの、特に幾何学的錯視については多くの種類が知られている。だまし絵とは異なる原理による。
おもな幾何学的錯視
[編集]ミュラー・リヤー錯視
[編集]
ミュラー・リヤー錯視 (Müller-Lyer illusion) はミュラー・リヤーが1889年に発表した錯視[3]。線分の両端に内向きの矢羽を付けたもの(上段)と外向きの矢羽を付けたもの(中段)の線分は、上段が短く、中段は長く感じる[3]が、実際は同じ長さである。この錯覚が発生する説明は様々な側面から行われているが、有名な説明として、グリゴリーが1963年に発表した線遠近法が挙げられる[3]。
また、この錯覚を応用したものとして、ジャッドの図形が挙げられる[4]。 ジャッドの図形は、線分の中央に中点を打ち、両端に異なる向きの矢羽を付けると、外向きの矢羽が付けられた側に中点がずれて見えるという錯覚が用いられた図形である[4]。 このような錯視を「大きさの錯視」という[5]。
ツェルナー錯視
[編集]
非常に有名な錯視の一つ。図にある4本の線分は全て平行である。羽の角度が鈍角であるほど、錯視は顕著になる。このような錯視を「方位の錯視」という。
ヘリング錯視
[編集]
上の2本の平行線は、斜線の影響を受けてゆがんで見える。このような錯視を「湾曲の錯視」ともいう。湾曲の錯視では他にオービソン錯視、ヴント錯視などが該当する。
ポンゾ錯視
[編集]
二つに交わる線分の間に平行線を入れると、上の平行線が長く見える。錯視の発生は決して強くないが、一般によく知られる錯視の一つ。また、同視の錯視にはポンゾの円筒がある。なお、この錯視に関しては過去にリップスが発表を行っているが、現在ではポンゾ錯視というのが一般的。
フィック錯視
[編集]
フィック錯視 (Fick illusion) はフィック (Fick) によって1851年に示された、同じ長さの図形は縦にされたものが横にされたものより長く感じるという錯視[6][7]。 右の図形「A」と「B」は合同であるが、図形Bの方が長く見える。また、図形Aの方が太く見える。これは一般に、水平な横線より垂直な縦線の方が長く認識されるために起こるとされるが、この図形を90度傾けても図形Bの方が長く見えるため、詳しいメカニズムはまだ解明されていない。垂直水平錯視 (vertical-horizontal illusion, V-H illusion) ともいわれる[7]。
ポッゲンドルフ錯視
[編集]
斜線を描き、その間の形跡を別の図形で隠すと、その直線の始まりと終わりがずれて見える錯視で、よく知られる錯視である。図ではAとつながっているのは、一見それらしく見えるBではなく、Cが正しい。なお、この錯視はミュラーリヤーが投稿した論文の中から、審査員であったポッゲンドルフが発見したものであり、彼はミュラーにこの発見も付け加えるように依頼したが、ミュラーが気を利かせ、事実上の発見者であるポッゲンドルフの名前を冠して論文発表したといわれている。
デルブーフ錯視
[編集]
デルブフ錯視とも言われる。2つ合同な円を描き、片方には外に大きな同心円、もう片方には外に小さな同心円を描くと、元の円の大きさが異なって見える錯視。大きさが極端なほど錯視も顕著になる。応用として、図形の中から別の図形をくりぬくと、くりぬいた部分が大きく見える。円以外に、他の図形(正多角形など)でも発生する。
オッペル・クント錯視
[編集]
まずは等間隔に3本の平行線を引き、それぞれA、B、Cとする。AとBの間には何本もの平行線を引き、BとCの間には何も引かない。すると、AとBの間隔の方が広く見える。図の線分ABと線分BCの距離は同じである。なお、最初に文献にて提示したのはオッペルであるが、後にクントが量的研究を行ったことから、今日では先駆者の2人の名を連ねてこう呼ぶのが一般的である[8]。
フレイザー錯視
[編集]
フレイザー錯視は、イギリスの心理学者ジェームス・フレイザーが1908年に発表した錯視[9]。中央を共有する複数の円の上に傾き錯視が現れるようにすることで得られ、同心円が渦巻きのように見えるようになる[9]。これは、水平から若干傾けた斜線を平行に置くことで、全体としては水平であるはずの直線が、傾き方向に傾いて見える現象を利用している[10]。
なお、直線でも同じ錯視は現れ、傾いて見える。また、他の傾き錯視を用いてもフレイザー錯視のような渦巻き錯視の作図が可能であることが示されている[9]。
ミュンスターバーグ錯視・カフェウォール錯視
[編集]
平行線の両側に等間隔に同じ色の正方形を描く(上下互い違いになるようにする)。すると、平行なはずの線分が歪んで見える。カフェウォール錯視はその線分が灰色になったもので、より屈折度が高まる。
エビングハウス錯視
[編集]
同じ大きさの図形でも、大きい物の周りに置かれると小さく、小さい物の周りに置かれると大きく見える錯視。円形、球体が最も効果が現れる。また、エビングハウスは他の錯視も発表しているため、エビングハウスの大きさ錯視ともいう。
ジャストロー図形
[編集]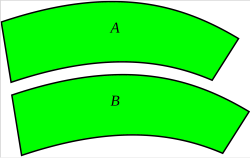
ジャストロー錯視ともいう。アメリカの心理学者のジャストローが発見したものである。上の図で、二つの扇形では内側、即ち下の扇形の方が大きく見える。また、その応用で台形を上下に並べると必然的に上の台形が大きく見える。
その他の幾何学的錯視
[編集]- ヴント錯視
- ヘリング錯視の逆に当たる。今度は平行線が反り返って見える。
- オービソン錯視
- ヘリング錯視と同じ原理で、同心円の上に描かれた正方形がゆがんで見える。
- ザンダー錯視
- 同じ長さの対角線が描く平行四辺形の形によって、別の長さに見える(鈍角の方が長く見える)錯視。
- ボールドウィン錯視
- 同じ長さの平行な線分を描き、片方の始点と終点には大きな図形を、もう片方には小さな図形を描くと、線分が異なった長さに見える錯視。
- ジャッド錯視
- 二等分線の両端に、片方は外向けに、もう片方は内向けに矢状の羽を付けると、等分されたはずの線分の長さが異なって見える。羽の角度が鋭いほど錯視は顕著になる。ミュラーリヤー錯視の一種といわれる。
- ヘフラーの図形
- 放射状の線の上に線分を引くと、曲がって見える錯視。任意に交差させた線分だと、なお効果的である。
- 盛永の錯視
- 垂直な線を描き、それに接する鋭角を左右対称に描く。垂直線を消せば、互いの鋭角の接点が垂直でなく見える。
- 小保内の角度錯視
- 垂直線の先端が、斜線が延長線上で交わるように線分を引いた場合、斜線が実際の交点より内側に見える。ポッゲンドルフ錯視の一種。
- 内藤の重力レンズ錯視
- 平行四辺形の交点4箇所にドットを打ち、その周辺に任意の円を描く(接してはいけない)。すると、平行四辺形がいびつな四角形に見える。1991年に内藤率いるNTTの研究グループが発表した。
- レニー錯視
- 斜めの線に接するように45度角を描く。同じ角度なのに、上下で角度が異なって見える。
- ブルンズウィック錯視(ヘフラーの湾曲対比)
- 二つの緩やかな彎曲線を描き、それを強い彎曲線と弱い彎曲線で囲ってやると、弱い彎曲線の方が曲がりが強く見える。ヘフラー彎曲対比とも呼ばれる。
- エーレンシュタイン錯視
- 田の図形で十字に交わる線分の交点部分を消すと、その周りに円形が浮かび上がる錯視。
- リップスの方向錯視
- 平行な三本線を引き、外側の2つの直線の両端に屈折した平行線を描く。すると三本線の真ん中が平行ではない線分に見えてしまう。
- リップスの湾曲錯視
- 大きさの異なる円を水平線上に並べる。真ん中を大きく端を小さく揃えると、水平線が弧を描いているように見える錯視。
- シェリー錯視
- 等間隔の片方は短い、もう片方は長い二組の平行線を描く。短い平行線の方が間隔が広く見える。この錯視は他の学者も発表しているが、当文献ではシェリーが一番古いとされる。
- ザンフォリン錯視
- 円形を二つ描き、その円の間と円の直径を等しくする。すると、両円の間の方が広く見える。
- ウェイト・マッサロの錯視
- ミュラー・リヤー錯視の応用。合同な長方形に矢羽を付けた場合、内向の図形の方が縦の幅が広く見える。
- ヘルムホルツの正方形
- 合同の正方形を二つ描き、片方を縦縞、片方を横縞にして四辺を消してしまうと、縦縞は横長に、横縞は縦長に見えてしまう錯覚。
- プルドン錯視
- 鋭角の鋭い三角形2つを一直線上に斜めに並べると、折れ曲がって見える錯視。
- ジョバネッリの錯視
- 合同な二つの図形を並列させる。その中心にドットを打つ。すると、双方の点の位置が中心から外に逸れて見える。
- ギラム錯視
- 水平な直線を台形で遮り、間の軌跡を消すと、水平線がずれて見える錯視。ポッゲンドルフ錯視に類似している。
- デイの正弦錯視
- 平行線で正弦を描くと、弧の部分が短く見える。
- バーゲン錯視
- 白い対角線と黒い図形で囲まれた格子戸の交点上に、無数の黒点のスプライトが見える錯視。この錯視は斜め45度から見ると錯覚が弱まる[11]。
- カニッツァの三角形

カニッツァの三角形 - 描いてないはずの三角形が浮かび上がる錯視。形の残像を利用したもの。
- エイムスの窓
- 動きのある錯視。円筒の中を左右往復する平行四辺形が、回転する長方形にも見える錯視。
- メッツガーの図形
- 円を描き、両端を残して後ははみ出るように別の図形で隠すと、円が楕円形に見える。図形は縞模様の長方形だと、度合いが顕著になる。
- ネッカーの立方体
- 線分だけの立方体で全ての辺を描くと、2種類の図形に見える錯視。
- シュレーダーの階段
- 描いた階段が逆さの向きにも見える錯視。応用したものとして、クレーター錯視がある。
- クレーターの錯視
- 凸面の図形は凹面にも見えるという錯視。月面のクレーターが隆起した地形にも見えることから名付けられた。
- シェパードの錯視
- 2つの平行四辺形の片方を斜めに傾け、離して置くと異なった図形に見える錯視。
- 市松模様の錯視
- 市松模様が左、上に歪んで見える錯視。
- ルキーシュ錯視
- 重ならないように等間隔の正方形を二つ描く。その正方形の一頂点から対角線上の点を通る平行線を等間隔で引いていく。すると、対角線と交わる辺が飛び出し、正方形が歪な四角形に見える錯視。
- ロッド・フレーム錯視
- ロッドは棒、フレームは枠を表す。垂直線を一本描き、それを正方形で囲みその正方形を傾けていくと、垂直線も次第に傾いて見える錯視。発見者はAl Behとされている。
- トランスキー錯視
- 複数の円を任意的に一部分だけを切り出す。一つは三分の一ほど、他はそれより短く取っていく。すると、元の部分は合同であるはずなのに、より短く切り取られた曲線の方が平行に見えてしまう。
- ボッティ錯視
- 2種類存在する。
- 等しい垂直距離の図形を、一つは垂直線のみで、もう一つは斜線のみで構成する。すると、斜線のみの図形の方が間隔が長く見える錯視。
- 等しい垂直距離の図形を、一つは平行線のみ、もう一つは同じく平行線だが斜めにずらしていく。すると、斜めにずらした図形の方が間隔が短く見える錯視。
- ラスカ錯視
- 平行線の両端から、片方は鈍角に交わる直線を、もう片方には鋭角に交わる同じ長さの直線を引く。すると、鋭角に交わる直線の方が長く見える錯視。あまり知られていない錯視であるが、ミュラー=リヤー錯視の根本概念を覆す錯視であると記されている。
- ロエブ錯視
- 平行線上に、等しい直線を2つ取る。片方はその上に平行線を、もう片方には等間隔で下に平行線を引く。すると、元の2本の平行線がずれているように見える錯視。
- シューマン錯視
- 2つの図形の間隔が等しいとき、大きい図形に阻まれたものは狭く見え、狭い図形に阻まれたものは広く見える錯視。
- ヴィカリオ錯視
- 等間隔に垂直な縦棒を並べていき、2つの正方形(に見える形)を作る。片方は長い棒、もう片方は短い棒で作ると、短い棒で作った正方形の方が明らかに縦棒同士の間隔が広く見える錯視。
- ジェルビーノ錯視
- 任意の正多角形の頂点を隠すように合同な正三角形を規則的(必ず辺が交わるように)に置いていくと、元の多角形がずれて見える錯視。
- カラの正方形錯視
- 塗りつぶさないことが条件で、辺が太い2つの合同な正方形をぎりぎり辺に交わらないぐらいに2つ並べ、お互い平行線に沿ってずらしていくと、2つの正方形がお互い傾いて見える錯視。
- ビンナの角度錯視
- 2つの合同な正多角形を描き、その角と同じだけの黒く塗りつぶした長方形を用意する。片方には全ての頂点に交わるように長方形を敷いていき(ただし、多角形と交わった内側部分は消す)、もう一つは全ての辺に接するように長方形を敷いていく。すると、頂点と交わった正多角形の方がより角が鋭く見え、辺と交わった正多角形はより円形に見える。
- 和田・田中の角度錯視
- 同角度の鋭角を持つ図形を2種用意し、片方は線分を短く、もう片方は線分を長くする。すると線分が短い方が、より鋭角気味に見える錯視。
- ギブソン錯視
- 任意の平行線を引き、その間に弧を描くと、平行線が弧と反対向きの弧状に見える錯視。また、合同な弧を二本描き、その始点と終点の接点上を始点と終点にした線分を描くと、その線分も弧状に見える。
- 提灯の錯視
- 心理学者北岡明佳が発表した錯視。合同な円形でも、斜線に囲まれた円は囲まれていない円より小さく見える錯視。形が提灯に似ていることから名付けられた。
ポップル錯視(文字列傾斜錯視)
[編集]平行に並べた図形の模様を均等に上下にずらすと、図形が傾いて見える錯視。ツェルナー錯視のように並べると顕著になる。ある種の活字体で可視化された文字列にも、この傾向が見られるパターンがあることが知られている。「杏マナー」という文字列を繰り返し並べると、右下がりに見える。北岡明佳がポップル錯視との類似を指摘した。この錯視は、単なるインターネットメディアの話題にとどまらず、国内錯視研究の第一人者でもある北岡のホームページでも「読み人知らず」として採り上げられているほか、新井仁之がこの錯視を『文字列傾斜錯視』と定義して、ウェーブレットを利用してこの現象を起こす文字列を見出したり、錯視現象をキャンセルしたり強化したりするといった論文を発表している[12]。また、「アロマ企画」「コニア画」「科研交付」[13]「下广卞廿十亠卉与本二上旦上二本与卉亠十廿卞广」の文字列でも、この錯視が発生する。
色に関する錯視
[編集]色の錯視
[編集]
- 色の対比
- 色の同化
- マッハバンド
- シュブルール錯視 : マッハの帯と混同されることが多い。
- パザルリ錯視
- ムンカー錯視
- ネオン色拡散
- ベンハムの独楽 : 白と黒で塗り分けた独楽を回すと、色感覚が生まれるという錯視。
色の同化
[編集]背景の色は全て同じであるが、元の色よりも線の色に似た傾向の色に見える。これを色の同化という[14]。
この画像の作成においてAとBのタイルに使われている色は同じである。これはマサチューセッツ工科大学のエドワード・エーデルソン教授が考えた「チェッカーシャドウ錯視」というものである。
錯視の原因
[編集]錯視の原因は錯視によってそれぞれ違うと考えられている。たとえば、エニグマ錯視はマイクロ・サッケードが引き起こしている[15]。
しかし、多くの錯視は原因が分かっておらず、仮説が立てられているというものがほとんどである(例:ムンカー錯視、詳細は[16])。
脚注
[編集]- ^ "錯視は錯覚の一種であり,視覚に関するものである。... 錯視とは知覚レベルのものである。" p.289 より引用。北岡明佳. (2012). 近年の錯視研究の展開 ― 巻頭言に代えて ―. 心理学評論, 55巻 3号 pp. 289-295.
- ^ 文部省、日本心理学会編『学術用語集 : 心理学編』日本学術振興会、1986年。ISBN 4-8181-8602-3。
- ^ a b c 北岡明佳 2010, p. 2.
- ^ a b ジャック・ニニオ 2004, p. 128.
- ^ 北岡明佳 2010, p. 1.
- ^ Oppelによって1855年に示されたのが最初とする資料も存在する。これは、Oppelがフィック錯視を錯視として研究した初の研究者であることによる。
- ^ a b 北岡明佳 2010, p. 10.
- ^ 北岡明佳 2010, p. 8.
- ^ a b c 北岡明佳 2010, p. 24.
- ^ “同心円の集まりなのに渦巻きに見える(フレーザー錯視)”, Newton別冊 脳はなぜだまされるのか? 錯視 完全図解 (ニュートン プレス): p. 94, (2007-10-01)
- ^ 北岡明佳 2007, p. 101.
- ^ 新井仁之; 新井しのぶ (2012年4月2日). “文字列傾斜錯視 作品集”. 錯視の科学館. 2015年2月24日閲覧。
- ^ 「科研交付」は北岡が考案したものである。
- ^ “色同化|学習支援ツール”. 色と光の能力テストTOCOL(トーコル). 2011年8月20日閲覧。
- ^ Brandon Keim (2008年11月21日). “Eye Flicker Explains 'Enigma' Optical Illusion” (英語). Wired Science. 2013年9月18日閲覧。
- ^ NTT物性科学基礎研究所. “錯視 色彩の錯視 ムンカー錯視”. Illusion Forum イリュージョンフォーラム. 2013年9月18日閲覧。
参考文献
[編集]- 後藤倬男・田中平八編 編『錯視の科学ハンドブック』東京大学出版会、2005年。ISBN 4-13-011115-9。 - 一連の幾何学錯視図形(ツェルナー、ポンゾ、ポッゲンドルフ、フィック、オッペル・クント、デルブーフ)は本編の参考図及び、各錯視における定義を参考に市販図形描画ツールにて作成した。また、その他の幾何学錯視における説明も本誌の凡例を参考にしたものである。
- 北岡明佳『錯視入門』朝倉書店、2010年6月30日。ISBN 9784254102260。全国書誌番号:21798667。
- ジャック・ニニオ 著、鈴木光太郎、向井智子 訳『錯視の世界 古典からCG画像まで』(初版)新曜社、2004年2月25日。
- 北岡明佳『だまされる視覚 錯視の楽しみ方』(初版)化学同人、2007年1月20日。ISBN 9784759813012。全国書誌番号:21264368。
関連項目
[編集]- 錯覚
- ハーマングリッド
- ホワイト効果
- ストロボ効果
- ホロウマスク錯視
- トロンプ・ルイユ
- 月#視覚的特徴
- 閃輝暗点
- 空目
- コリジョンコース現象
- ゲシュタルト心理学
- The dress - 青と黒のドレスが人によっては白と金色に見える写真
外部リンク
[編集]- “ILUSÕES DE ÓTICA” (ポルトガル語). 2013年9月18日閲覧。
- 科学技術振興機構. “マインド・ラボ”. JSTバーチャル科学館. 2013年9月18日閲覧。
- “Optical illusion” (英語). 2013年9月18日閲覧。
- 北岡明佳 (2013年9月16日). “北岡明佳の錯視のページ”. 立命館大学. 2013年9月18日閲覧。
- NTT物性科学基礎研究所. “錯視と錯聴を体験!Illusion Forum イリュージョンフォーラム”. 2013年9月18日閲覧。
- Visual Illusions - ウェイバックマシン(2007年9月29日アーカイブ分) - スカラーペディア百科事典「錯視」の項目。


 French
French Deutsch
Deutsch




