Brewsterhoek

In de optica wordt onder de brewsterhoek of polarisatiehoek verstaan de invalshoek waarbij volledige polarisatie optreedt. Hij is vernoemd naar de Schotse natuurkundige David Brewster (1781-1868). Als licht het grensvlak tussen twee stoffen met verschillende brekingsindices kruist, wordt een deel ervan weerkaatst en een ander deel gebroken aan het grensvlak. Bij een bepaalde invalshoek wordt alleen licht weerkaatst dat evenwijdig aan het grensvlak gepolariseerd is. Deze invalshoek heet de brewsterhoek . De weerkaatste, zuiver gepolariseerde bundel staat dan loodrecht op de gebroken bundel.
P- en s-polarisatie
[bewerken | brontekst bewerken]Er worden twee polarisaties (polarisatierichtingen) van het licht ten opzichte van het grensvlak onderscheiden:
- p-gepolariseerd licht. De trilling van het elektrische veld van het licht ligt in het vlak van de bijgaande figuur, dus in het vlak van de invallende straal en de normaal aan het grensvlak tussen de twee stoffen. De p in p-gepolariseerd betekent parallel.
- s-gepolariseerd licht, met een polarisatie haaks op die van p-gepolariseerd licht. De trilling van het elektrische veld van dit licht staat haaks op het vlak van de bijgaande figuur en loopt dus evenwijdig aan het grensvlak tussen de twee stoffen. De s in s-gepolariseerd betekent senkrecht (Duits: loodrecht). In Nederlandse natuurkundeboeken (bijvoorbeeld van Kronig) wordt s-gepolariseerd licht ook wel l-trilling genoemd, met l van loodrecht.
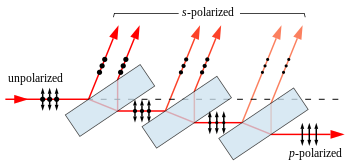
Als ongepolariseerd licht onder de brewsterhoek invalt op het grensvlak is het weerkaatste licht zuiver s-gepolariseerd en het gebroken licht vooral p-, maar ook nog deels s-gepolariseerd.
Stralende dipolen
[bewerken | brontekst bewerken]Het natuurkunde principe kan kwalitatief begrepen worden uit de manier waarop elektrische dipolen reageren op p-gepolariseerd licht. Het invallende licht wordt geabsorbeerd aan het oppervlak en weer uitgestraald door de trillende elektrische dipolen aan het grensvlak van de twee media. De polarisatie van licht dat zich vrij voortplant is altijd loodrecht op de richting waarin dat licht zich beweegt. De dipolen die licht uitstralen trillen in de richting van die polarisatie. Maar de dipolen kunnen geen energie uitstralen in de richting waarin ze trillen.
Daaruit volgt dat als de voortplantingsrichting van het gebroken licht loodrecht staat op de voortplantingsrichting van het weerkaatste licht de dipolen geen weerkaatst licht zullen uitstralen. Omdat de s-polarisatie evenwijdig ligt aan het grensvlak tussen de media, kunnen de overeenkomstig trillende dipolen alleen licht uitstralen in de richting van het weerkaatste licht. Daarom bestaat er geen brewsterhoek voor invallend s-gepolariseerd licht: dit wordt onder alle invalshoeken weerkaatst als s-gepolariseerd licht.
Berekening
[bewerken | brontekst bewerken]Het licht loopt van stof (medium) 1 naar stof 2. De voorwaarde van Brewster luidt
met de invalshoek in stof 1 en de brekingshoek (refractiehoek) in stof 2.
Met de Wet van Snellius
waarin en de brekingsindices van de twee media 1 en 2 voorstellen, kunnen we de invalshoek berekenen, waarbij de polarisatie van het weerkaatste licht totaal is.
- .
Na herschikking krijgen we:
of
- .
Deze vergelijking heet de wet van Brewster.
Voorbeeld
[bewerken | brontekst bewerken]Omdat alle p-gepolariseerde licht gebroken wordt, moet al het licht dat aan het oppervlak weerkaatst wordt bij deze hoek s-gepolariseerd zijn. Een stuk glas kan dus gebruikt worden om te polariseren, als de invalshoek precies de brewsterhoek is. Omdat de brekingsindex n voor een gegeven medium afhangt van de golflengte van het licht, doet de brewsterhoek dat ook.
- Voor een stuk gewoon glas in lucht is n2/n1 = 1,51 (rood en geel licht) en is de brewsterhoek 56,5°.
- Voor water onder lucht is n2/n1 = 1,330 (rood licht) en is de brewsterhoek 53,1°.
Geschiedenis
[bewerken | brontekst bewerken]Het verschijnsel dat licht gepolariseerd wordt bij weerkaatsing onder een bepaalde hoek werd voor het eerst waargenomen door Etienne-Louis Malus in 1808. Hij probeerde tevergeefs deze hoek te verklaren uit de brekingsindex van het materiaal, maar de kwaliteit van het glas liet te wensen over. In 1815 experimenteerde Brewster met glas van een hogere kwaliteit. Hij toonde aan dat de hoek wel degelijk afhing van de brekingsindex en stelde zijn wet op.
Toepassingen
[bewerken | brontekst bewerken]
Polarisator
[bewerken | brontekst bewerken]Een eenvoudig polarisatiefilter is te maken door microscoopglaasjes op elkaar te leggen - zie figuur.
Brewstervenster
[bewerken | brontekst bewerken]Gaslasers gebruiken meestal een uittreevenster voor het licht dat onder de brewsterhoek staat, een zogenaamd brewstervenster. Het venster weerkaatst een deel van het s-gepolariseerde licht zijdelings maar niet het p-gepolariseerde licht. Daardoor wordt de versterking van de s polarisatie in de laser verminderd terwijl de p-polarisatie daar geen last van heeft. De laserbundel is daardoor p gepolariseerd en het venster geeft geen energieverlies[1]
Zie ook
[bewerken | brontekst bewerken]Literatuur
[bewerken | brontekst bewerken]- Born, M. & Wolf, E.: Principles of optics, Pergamon Press, Oxford, 1987
- Hecht, E. & Zajac, A.: Optics, Addison-Wesley, Reading, 1974
- Kronig, A. (red.): Leerboek der natuurkunde, Scheltema & Holkema, Amsterdam, 1962
- A. Lakhtakia, 'Would Brewster recognize today's Brewster angle?' OSA Optics News, Vol. 15, No. 6, pp. 14–18 (1989).
- A. Lakhtakia, 'General schema for the Brewster conditions,' Optik, Vol. 90, pp. 184–186 (1992).
- ↑ Optics, 3rd edition, Hecht, ISBN 0-201-30425-2


 French
French Deutsch
Deutsch









