Oppervlaktegetrouwe cilinderprojectie

De oppervlaktegetrouwe cilinderprojectie is een limietgeval van de oppervlaktegetrouwe kegelprojectie (een later ontwikkelde projectie met een extra vrijheidsgraad), namelijk met standaardparallellen (waar een vierkantje op Aarde wordt afgebeeld als een vierkantje, dus waar de kaart ook hoekgetrouw is) aan weerszijden van de evenaar, op dezelfde afstand, of met beide de evenaar.^[1]

Een vierkantje op Aarde aan de poolzijden van de standaardparallellen wordt afgebeeld als een liggende rechthoek, en tussen de standaardparallellen als een staande rechthoek.

Bij een oppervlaktegetrouwe cilinderprojectie van een gebied (bijvoorbeeld een land) kan men de standaardparallellen zo kiezen dat er één midden door het gebied gaat, de vervorming is dan het kleinst.^[2] (Met de oppervlaktegetrouwe kegelprojectie kunnen, met behoud van oppervlaktegetrouwheid, beide standaardparallellen echter onafhankelijk van elkaar gekozen worden, waardoor de vervorming nog meer gereduceerd kan worden.)

Als φ₁ de breedtegraad is van de noordelijke standaardparallel, en R is de straal van de Aarde, en oppervlaktes zijn op de kaart ${\displaystyle s^{2}}$ maal zo groot als op Aarde, dan is de breedte van de kaart ${\displaystyle 2\pi Rs\cos \phi _{1}}$ en de hoogte ${\displaystyle {\frac {2Rs}{\cos \phi _{1}}}}$.

Gegeven de geografische breedte ${\displaystyle \phi \,}$ en lengte ${\displaystyle \lambda \,}$ (in radialen) wordt de projectie gegeven door:

${\displaystyle x\,=(Rs\cos \phi _{1})\lambda }$

${\displaystyle y\,={\frac {Rs}{\cos \phi _{1}}}\sin \phi }$

De schaal^[3] in oostwestrichting is

${\displaystyle s{\frac {\cos \phi _{1}}{\cos \phi }}}$

en de noordzuidschaal

${\displaystyle s{\frac {\cos \phi }{\cos \phi _{1}}}}$

Bij de orthografische cilinderprojectie geldt ${\displaystyle \phi _{1}=0}$. De breedte van de kaart is ${\displaystyle 2\pi Rs}$ en de hoogte ${\displaystyle 2Rs}$.

Bij de projectie van Gall-Peters geldt ${\displaystyle \phi _{1}=\pi /4}$ (45 graden). De breedte van de kaart is ${\displaystyle \pi {\sqrt {2}}Rs}$ en de hoogte ${\displaystyle 2{\sqrt {2}}Rs}$. Bij gelijke breedte is deze kaart dus een factor twee verticaal uitgerekt, vergeleken met de hierboven genoemde kaart.

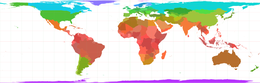
De orthografische cilinderprojectie of oppervlaktegetrouwe cilinderprojectie van Lambert is een meetkundige projectie van het aardoppervlak op een cilinder, bestaande uit projecties vanuit de punten op de omwentelingsas van de bol in richtingen loodrecht op de as. Naast een aantal andere projecties werd deze in 1779 voorgesteld door Johann H. Lambert.

De tropen zijn het minst vervormd. Daarbuiten is de kaart horizontaal uitgerekt.

James Gall presenteerde de projectie van Gall-Peters (petersprojectie) in 1855 en Arno Peters in 1967, en alhoewel er geen verschil is tussen de projectie van Peters en die van Gall, hield Peters toch vol dat het zijn eigen onafhankelijke idee was.

De oppervlaktegetrouwheid van deze projectie, waarbij ontwikkelingslanden er groter op kwamen te staan dan met de alom bekende mercatorprojectie het geval was, bracht de Unesco ertoe kaarten op basis van deze projectie uit te brengen.

Onder meer de Verenigde Staten en Europa zijn weinig vervormd, maar Zuid-Amerika, Afrika, Zuid-Azië en Australië zijn verticaal uitgerekt. In het gebied op het zuidelijk halfrond met weinig vertekening is er weinig land, niet veel meer dan het zuiden van Argentinië en het zuiden van Nieuw-Zeeland.

Andere orthografische projecties:

• Orthografische azimutale projectie

Andere cilinderprojecties:

• Afstandsgetrouwe cilinderprojectie
• Mercatorprojectie
• Universele transversale mercatorprojectie

Andere oppervlaktegetrouwe projecties:

• Oppervlaktegetrouwe kegelprojectie
• Oppervlaktegetrouwe azimutale projectie (azimutale projectie van Lambert)
• Mollweideprojectie
• Sinusoïdeprojectie
• Projectie van Bonne
• Projectie van Aitoff-Hammer