Pentagrampuzzel

Een pentagrampuzzel is een puzzel die gebruik maakt van een pentagram als regelmatige sterveelhoek.

Er kunnen globaal drie soorten pentagrampuzzels worden onderscheiden:

• Taalkundige pentagrampuzzel
• Rekenkundige pentagrampuzzel
• Mechanische pentagrampuzzel, bijvoorbeeld een draaibare kubus als variant van de Rubiks kubus of een puzzelspel met een metalen ring.^[1]

Een taalkundige pentagram is een variant van de anagrampuzzel. Er bestaan puzzels met enkelvoudige pentagrammen, maar ook met dubbele pentagramvormen. Vaak staan de letters in een dubbele ring om het pentagram.

Op de uiteinden van elk lijnstuk bevindt zich een letter, dus 10 letters in totaal. De tien letters vormen samen een anagram van het oplossingswoord. Dit woord kan gevonden worden door vanaf een bepaalde letter de lijnen van het pentagram te volgen. Dit kan linksom óf rechtsom gedaan worden. Door bij de juiste letter te beginnen wordt het oplossingswoord gevonden. Deze puzzelsoort is al oud. Er werd al in 1887 een dubbele pentagrampuzzel geplaatst in het Duitse familieblad Die Gartenlaube. Die puzzel verscheen onder de naam Druidenfuss (druïdenvoet).

• 
  Opgave 1
• 
  oplossing 1
• 
  opgave 2
• 
  oplossing 2

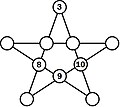
Een rekenkundige pentagrampuzzel bestaat uit vijf lijnstukken die onderling contact hebben in 10 punten. Deze punten dienen te worden gevuld met de getallen 1 t/m 10. ^[2] Elke lijn bezit vier getallen die samen de lijnsom vormen.

De opdrachten kunnen verschillend zijn, bijvoorbeeld: 1. Vul de lege cirkels met getallen zodat de som van de getallen langs elke lijn dezelfde waarde heeft. Soms zijn enkele cirkels vooraf ingevuld.^[3] 2. Het getal binnen de vijf driehoeken van de ster is gelijk aan de som van de drie getallen in de omringende cirkels. Het getal in het midden van de ster is gelijk aan de som van de vijf getallen in de omringende cirkels. De getallen in de cirkels kunnen alleen 0 tot 9 zijn en elk getal kan slechts één keer worden gebruikt. Als er 3 cirkels reeds zijn ingevuld, moeten de overige zeven getallen worden gevonden.

• Pentalfa