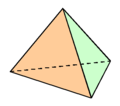
Regelmatig veelvlak

Een regelmatig veelvlak of platonisch lichaam is een veelvlak waarvan de zijvlakken regelmatige veelhoeken zijn. Regelmatige veelvlakken zijn convex, hun zijvlakken zijn congruent en alle hoeken tussen de vlakken zijn onderling gelijk. Er bestaan vijf regelmatige veelvlakken. De kubus is het bekendste voorbeeld. De vijf zijn: het viervlak, de kubus, het achtvlak, twaalfvlak en twintigvlak.

De regelmatige veelvlakken worden sinds de romantiek ook wel platonische lichamen genoemd, omdat ze voor het eerst door Plato zijn beschreven. De vijf regelmatige veelvlakken waren volgens de mythologie in Schotland in de steentijd bekend.^[1] Pythagoras wist in 520 v.Chr. van het bestaan van drie van de vijf regelmatige veelvlakken af: het viervlak, de kubus en het regelmatige twaalfvlak. Plato bracht de vijf regelmatige veelvlakken in verband met de vijf kosmische bouwstenen van de wereld: vuur, lucht, water, aarde en hemelmaterie. Kepler bracht ze twee millennia later, in de tussentijd waren de halfregelmatige veelvlakken al ontdekt, in verband met de structuur van het zonnestelsel. Behalve de Aarde waren in die tijd vijf planeten bekend. Daarin vergiste hij zich.

Euclides wist al dat er vijf convexe regelmatige veelvlakken waren.

• 
  viervlak
• 
  kubus
• 
  regelmatig achtvlak
• 
  regelmatig twaalfvlak
• 
  regelmatig twintigvlak

Dit valt in te zien met het volgende bewijs:

Een regelmatig veelvlak wordt volledig bepaald door het soort van regelmatige veelhoek en het aantal van die veelhoeken, dat in een hoekpunt bij elkaar komt. Bovendien moeten de hoeken die in één hoekpunt samenkomen samen minder dan 360° zijn. Dit kunnen drie driehoeken: 3×60°=180°, vier driehoeken 240° of vijf driehoeken 300° zijn, maar niet meer. Het kunnen ook drie vierkanten: 3×90°=270° of drie vijfhoeken: 3×108°=324° zijn. Lichamen met zes driehoeken: 6×60°=360°, vier vierkanten: 4×90°=360°, met drie zeshoeken: 3×120°=360° of met regelmatige veelhoeken met nog meer hoekenpunten zijn onmogelijk.

Er zijn ontaarde regelmatige veelvlakken denkbaar met maar twee zijvlakken in een hoekpunt of zes driehoeken in ieder hoekpunt. In beide gevallen wordt het een platte figuur,

Verbindt men de middens van de zijvlakken van een regelmatig veelvlak met elkaar, dan vormen de verbindingslijnen de ribben van een ander veelvlak. Een viervlak blijft een viervlak, maar een kubus wordt een achtvlak en omgekeerd. Een twaalfvlak wordt een twintigvlak en omgekeerd. De kubus en het achtvlak zijn het duale veelvlak van elkaar, het twaalfvlak en het twintigvlak ook. De definitie van een duaal veelvlak zegt niet dat de middens van de zijvlakken van dat veelvlak moeten worden genomen om het duale veelvlak te construeren, maar bij de regelmatige veelvlakken gaat het op deze manier wel.

Kiest men vier hoekpunten van een kubus, zodanig dat geen twee hoekpunten op dezelfde ribbe van de kubus liggen, en verbindt men ze met elkaar, dan vormen de verbindingslijnen de ribben van een regelmatig viervlak. De systematische naam van een kubus, in lijn met de volgende regelmatige veelvlakken, is regelmatig zesvlak.

Er kunnen met ieder regelmatig veelvlak drie bollen worden geassocieerd: de ingeschreven bol rakend aan de zijvlakken, de bol rakend aan de ribben en de omgeschreven bol rakend aan de hoekpunten.

Een kenmerk van een regelmatig veelvlak is dat in ieder hoekpunt even veel vlakken samenkomen. Hierbij zijn drie, vier of vijf vlakken mogelijk. De wiskundige Leonhard Euler gaf al in de 18e eeuw een formule voor het verband tussen het aantal hoekpunten, ribben en zijvlakken van een veelvlak: ${\displaystyle H-R+Z=2}$.

Het aantal vlakken per hoekpunt wordt ook de valentie van dat hoekpunt genoemd.

Nederlandse naam	Griekse naam	Afbeelding	Hoekpunten per vlak	Vlakken per hoekpunt, valentie	Vlakken	Ribben	Hoekpunten	Schläfli-symbool	Symmetriegroep
viervlak	tetraëder		3	3	4	6	4	{3, 3}	Td
kubus	hexaëder		4	3	6	12	8	{4, 3}	Oh
regelmatig achtvlak	octaëder		3	4	8	12	6	{3, 4}	Oh
regelmatig twaalfvlak	dodecaëder		5	3	12	30	20	{5, 3}	Ih
regelmatig twintigvlak	icosaëder		3	5	20	30	12	{3, 5}	Ih

${\displaystyle z}$ zijden per vlak
${\displaystyle h}$ vlakken per hoekpunt
${\displaystyle Z}$ vlakken
${\displaystyle R}$ ribben
${\displaystyle H}$ hoekpunten

Het verband tussen ${\displaystyle Z}$, ${\displaystyle z}$ en ${\displaystyle h}$ wordt gegeven door de formule:

${\displaystyle Z={\cfrac {2}{1-z\times \left({\cfrac {1}{2}}-{\cfrac {1}{h}}\right)}}={\cfrac {4h}{2(h+z)-zh}}}$

• (b) - Het aantal ribben ${\displaystyle R}$ van een veelvlak, regelmatig of niet, is gelijk aan het aantal zijden per vlak ${\displaystyle z}$ maal de helft van het aantal zijvlakken ${\displaystyle Z}$, want elke ribbe wordt gedeeld door de twee aangrenzende vlakken.
• (c) - Het aantal hoekpunten ${\displaystyle H}$ van een veelvlak is gelijk aan het aantal vlakken ${\displaystyle Z}$ maal het aantal zijden per vlak ${\displaystyle z}$ gedeeld door het aantal zijvlakken dat in een hoekpunt samenkomt.

De vergelijking kan uit de onderstaande drie worden afgeleid:

${\displaystyle Z=R-H+2}$	(a)
${\displaystyle R={\cfrac {Z\times z}{2}}}$	(b)
${\displaystyle H={\cfrac {Z\times z}{h}}}$	(c)

Vervang in (a) ${\displaystyle R}$ door (b) en ${\displaystyle H}$ door (c). Na vereenvoudiging levert dat de bovengenoemde formule voor ${\displaystyle Z}$ op.

Behalve regelmatige bestaan er ook halfregelmatige veelvlakken.

Bij een ruimere definitie van veelvlak, waaronder ook zelfdoorsnijdende en samengestelde veelvlakken vallen, is een regelmatig veelvlak een veelvlak dat hoekpunt-, ribbe- en zijvlaktransitief is. Er zijn dan 14 regelmatige veelvlakken: de vijf regelmatige veelvlakken, die het onderwerp van dit artikel zijn, de vier kepler-poinsot-lichamen en vijf regelmatige samengestelde veelvlakken.