Espaço métrico – Wikipédia, a enciclopédia livre

Este artigo não cita fontes confiáveis. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW  • CAPES  • Google (notícias • livros • acadêmico) (Agosto de 2012)

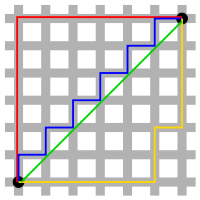
Em matemática, um espaço métrico é um conjunto onde a distância entre quaisquer dois de seus elementos é definida por uma função chamada métrica.^[1] A métrica permite que a noção de continuidade seja estendida para funções entre espaços métricos. Os espaços métricos são exemplos de uma classe mais abrangente de espaços, chamados espaços topológicos.

O espaço métrico mais familiar é o espaço euclidiano. Na verdade, a métrica é uma generalização das quatro propriedades conhecidas da distância euclidiana. A métrica euclidiana define a distância entre dois pontos como o comprimento do segmento de reta que os conecta.

Existem outros espaços métricos, por exemplo, na geometria elíptica. Mesmo no espaço euclidiano, podemos adotar uma medida diferente de distância, como a métrica de Manhattan.

Seja ${\displaystyle X}$ um conjunto qualquer. Uma métrica definida sobre ${\displaystyle X}$ é uma função ${\displaystyle d:X\times X\to \mathbb {R} }$ que associa um par ${\displaystyle (x,y)\in X\times X}$ ao número ${\displaystyle d(x,y)}$, chamado de distância entre ${\displaystyle x}$ e ${\displaystyle y}$, de modo que para quaisquer ${\displaystyle x,y,z\in X}$ valem:

1. ${\displaystyle d(x,y)=0\iff x=y}$;
2. Se ${\displaystyle x\neq y}$, então, ${\displaystyle d(x,y)>0}$ (positividade);
3. ${\displaystyle d(x,y)=d(y,x)}$ (simetria);
4. ${\displaystyle d(x,z)\leq d(x,y)+d(y,z)}$ (desigualdade triangular).

Um par ${\displaystyle (X,d)}$ em que ${\displaystyle X}$ é um conjunto e ${\displaystyle d}$ é uma métrica é chamado de espaço métrico.^[2]

De forma intuitiva, pode-se pensar no conjunto ${\displaystyle X}$ como um conjunto de locais ligados por um sistema de estradas. A distância entre dois pontos pode ser definida como o comprimento da rota mais curta que liga dois desses locais. Deste modo, a simetria significa que neste sistema de estradas não deve haver estradas de mão única e a desigualdade do triângulo expressa o fato de que os desvios não são atalhos.

• O conjunto ${\displaystyle \mathbb {R} }$ dos números reais é o exemplo mais importante de espaço métrico com respeito à métrica ${\displaystyle d(x,y)=|x-y|}$
• ${\displaystyle (\mathbb {R} ^{n},d)}$, onde ${\displaystyle d((x_{1},\ldots ,x_{n}),(y_{1},\ldots ,y_{n}))={\sqrt {(y_{1}-x_{1})^{2}+\cdots +(y_{n}-x_{n})^{2}}}}$, é o espaço de dimensão ${\displaystyle n\,}$ com a distância usual (espaço vetorial euclidiano).
• ${\displaystyle (\mathbb {R} ^{n},d)}$, onde ${\displaystyle d(x,y)=\max\{|x_{1}-y_{1}|,...,|x_{n}-y_{n}|\}}$ observe que com esse exemplo, olhar para um mesmo conjunto ${\displaystyle X}$ com métricas diferentes. Isso provoca uma mudança na topologia do conjunto.
• ${\displaystyle (X,d)\,}$, onde ${\displaystyle d(x,y)=\left\{{\begin{matrix}0,&{\mbox{se }}x=y\\1,&{\mbox{se }}x\neq y\end{matrix}}\right.}$ é denominado de espaço métrico discreto.
• Qualquer subconjunto ${\displaystyle A\subset X}$de um espaço métrico ${\displaystyle X}$ é um espaço métrico, basta considerar a restrição ${\displaystyle d|_{A\times A}\to \mathbb {R} }$.
• Seja V o conjunto das funções contínuas de domínio ${\displaystyle [a,b]}$ e contradomínio real. Então ${\displaystyle d(f,g)=\max |f(x)-g(x)|\,}$ torna V um espaço métrico (a condição de continuidade é importante para garantir que essa métrica seja definida).

Qualquer Espaço vetorial munido de uma norma ${\displaystyle \lVert \cdot \rVert }$ é um espaço métrico. Seja ${\displaystyle {\mathsf {E}}}$ um espaço vetorial. Uma norma em ${\displaystyle {\mathsf {E}}}$ é uma função | |: ${\displaystyle {\mathsf {E}}}$ ${\displaystyle \rightarrow }$ ${\displaystyle \mathbb {R} }$, que associa cada vetor ${\displaystyle {\boldsymbol {x}}}$ ${\displaystyle \in }$ ${\displaystyle {\mathsf {E}}}$ o número real ||${\displaystyle {\boldsymbol {x}}}$|| chamada a norma de ${\displaystyle {\boldsymbol {x}}}$, de modo a serem cumpridas as condições abaixo para quaisquer ${\displaystyle {\boldsymbol {x}}}$, ${\displaystyle {\boldsymbol {y}}}$ ${\displaystyle \in }$ ${\displaystyle {\mathsf {E}}}$ e ${\displaystyle \lambda }$ escalar^[3]:

1. Se ${\displaystyle {\boldsymbol {x}}}$ ${\displaystyle \neq }$ 0 então ||${\displaystyle {\boldsymbol {x}}}$|| ${\displaystyle \neq }$ 0 ;
2. ||${\displaystyle \lambda }$${\displaystyle \cdot }$ ${\displaystyle {\boldsymbol {x}}}$|| = |${\displaystyle \lambda }$| ${\displaystyle \cdot }$||${\displaystyle {\boldsymbol {x}}}$|| ;
3. || ${\displaystyle {\boldsymbol {x}}}$ + ${\displaystyle {\boldsymbol {y}}}$ || ${\displaystyle \leq }$ ||${\displaystyle {\boldsymbol {x}}}$|| + ||${\displaystyle {\boldsymbol {y}}}$||

Todo espaço vetorial normado (${\displaystyle {\mathsf {E}}}$, |${\displaystyle \cdot }$ | ) torna-se um espaço métrico por meio da definição ${\displaystyle d(x,y)=||x-y||}$. Esta métrica diz-se proveniente da norma |${\displaystyle \cdot }$| . As propriedades 1 a 4 das distâncias são válidas para distâncias(métricas) que provém de normas. Essas propriedades resultam imediatamente das propriedades da norma. ^[4]

1. ${\displaystyle d(x,y)=||x-y||=0\Leftrightarrow x=y}$
2. Se ${\displaystyle x\neq y}$ então ${\displaystyle d(x,y)=||x-y||>0}$ pois ${\displaystyle x\neq y}$ ${\displaystyle \Rightarrow 0=||(x-y)-(x-y)||\leq ||x-y||+||y-x||=2.||x-y||}$ e ${\displaystyle x\neq y\Rightarrow ||x-y||\neq 0}$
3. ${\displaystyle d(x,y)=||x-y||=|-1|.||y-x||=||y-x||=d(y,x)}$
4. ${\displaystyle d(x,z)=||x-z||=||x+y-y-z||\leq ||x-y||+||y-z||=d(x,y)+d(x,z)}$ ^[5]

Definição. Sejam ${\displaystyle (X,d)}$ um espaço métrico e ${\displaystyle U\subset X}$ um subconjunto, diz-se que ${\displaystyle U}$ é um subconjunto aberto de ${\displaystyle X}$ quando para todo elemento ${\displaystyle x_{0}\in U}$ existe algum ${\displaystyle \epsilon >0}$ tal que ${\displaystyle x\in U}$ sempre que ${\displaystyle d(x,x_{0})<\epsilon }$.

Uma classe importante de conjuntos abertos são as chamadas bolas abertas, para um ponto ${\displaystyle x_{0}\in X}$ e um número real ${\displaystyle r>0}$, chama-se bola aberta de centro ${\displaystyle x_{0}}$e raio ${\displaystyle r}$ o subconjunto ${\displaystyle B(x_{0};r)=\{x\in X:d(x,x_{0})<r\}}$. Pode-se mostrar que toda bola aberta é um subconjunto aberto e que todo subconjunto aberto pode ser escrito como a reunião de uma família (enumerável ou não) de bolas abertas.

A classe dos conjuntos abertos gozam das seguintes propriedades:

1. O conjunto vazio ${\displaystyle \varnothing }$ e ${\displaystyle X}$ são subconjuntos abertos de ${\displaystyle X}$;
2. Se ${\displaystyle \{U_{\lambda }\}_{\lambda \in \Lambda }}$ é uma família indexada de subconjuntos abertos de ${\displaystyle X}$, então a reunião ${\displaystyle \bigcup _{\lambda \in \Lambda }U_{\lambda }}$ é também um subconjunto aberto de ${\displaystyle X}$;
3. Se ${\displaystyle U_{1},U_{2},\dots ,U_{n}}$são subconjuntos abertos de ${\displaystyle X}$, então a interseção ${\displaystyle \bigcap _{k=1}^{n}U_{k}}$ é também um subconjunto aberto de ${\displaystyle X}$.

As propriedades 1, 2 e 3 acima caracterizam a classe ${\displaystyle \tau \subset {\mathcal {P}}(X)}$ dos subconjuntos abertos de ${\displaystyle X}$ como uma topologia, chamada de topologia induzida pela métrica ${\displaystyle d}$, de modo que o par ${\displaystyle (X,\tau )}$ é um espaço topológico.^[2]

Definição. Um ponto ${\displaystyle a}$ que pertence a um subconjunto ${\displaystyle A}$ de um espaço métrico ${\displaystyle M}$ é dito um ponto aderente de ${\displaystyle A}$ quando, para todo ${\displaystyle \varepsilon >0}$, podemos encontrar ${\displaystyle x\in A}$ tal que ${\displaystyle d(x,a)<\varepsilon }$ .

O fecho(ou aderência) de um conjunto ${\displaystyle A}$ num espaço métrico ${\displaystyle M}$ é o conjunto ${\displaystyle {\bar {A}}}$ dos pontos de ${\displaystyle M}$ que são aderentes a ${\displaystyle A}$. Portanto, escrever ${\displaystyle a\in {\bar {A}}}$ é o mesmo que afirmar que o ponto ${\displaystyle a}$ é aderente a ${\displaystyle A}$ em ${\displaystyle M}$.^[6]

Diz-se que um conjunto ${\displaystyle F\subset M}$ é fechado no espaço métrico ${\displaystyle M}$ quando seu complementar ${\displaystyle M-F}$ é aberto em ${\displaystyle M}$. Podemos também definir um conjunto fechado como sendo um conjunto ${\displaystyle F\subset M}$ tal que ${\displaystyle F={\bar {F}}}$. Pode-se mostrar que essas definições são equivalentes.^[7]

Os subconjuntos fechados de um espaço métrico ${\displaystyle M}$ gozam das seguintes propriedades:

1. O conjunto vazio ${\displaystyle \varnothing }$ e o espaço inteiro ${\displaystyle M}$ são fechados;
2. A reunião ${\displaystyle F=F_{1}\cup ...\cup F_{n}}$ de um número finito de subconjuntos fechados ${\displaystyle F_{1},...,F_{n}\subset M}$ é um subconjunto fechado de ${\displaystyle M}$.
3. A interseção ${\displaystyle F=\bigcap F_{\lambda }}$ de uma família qualquer ${\displaystyle (F_{\lambda })_{\lambda \in L}}$ (finita ou infinita) de subconjuntos fechados ${\displaystyle F_{\lambda }\subset M}$ é um subconjunto fechado de ${\displaystyle M}$.^[8]

Definição. Sejam ${\displaystyle M,N}$ espaços métricos. Diz-se que a aplicação ${\displaystyle f:M\longrightarrow N}$ é contínua no ponto ${\displaystyle a\in M}$ quando, para todo ${\displaystyle \varepsilon >0}$ dado, é possível obter ${\displaystyle \delta >0}$ tal que ${\displaystyle d(x,a)<\delta }$ implica ${\displaystyle d(f(x),f(a))<\varepsilon }$ .

Diz-se que ${\displaystyle f:M\longrightarrow N}$ é contínua quando ela é contínua em todos os pontos ${\displaystyle a\in M}$ .

Equivalentemente, ${\displaystyle f:M\longrightarrow N}$ é contínua no ponto ${\displaystyle a\in M}$ quando, dada qualquer bola ${\displaystyle B'=B(f(a),\varepsilon )}$ de centro ${\displaystyle f(a)}$, pode-se encontrar uma bola ${\displaystyle B=B(a,\delta )}$ , de centro ${\displaystyle a}$, tal que ${\displaystyle f(B)\subset B'}$.^[9]

Exemplos.

1. Dada ${\displaystyle f:M\longrightarrow N}$, suponhamos que exista uma constante ${\displaystyle c>0}$ (chamada constante de Lipschitz) tal que ${\displaystyle d(f(x),f(y))\leq c\cdot d(x,y)}$ para quaisquer que sejam os ${\displaystyle x,y\in M}$. Dizemos então que ${\displaystyle f}$ é uma aplicação lipschitziana. Neste caso, ${\displaystyle f}$ é contínua. Com efeito, dado ${\displaystyle \varepsilon >0}$, tomemos ${\displaystyle \delta =\varepsilon /c}$. Então ${\displaystyle d(x,a)<\delta \Rightarrow d(f(x),f(a))\leq c\cdot d(x,a)<c\cdot \varepsilon /c=\varepsilon }$ .^[10]
2. Dado um ${\displaystyle a\in M}$ que seja ponto isolado de ${\displaystyle M}$ (isto é, um elemento ${\displaystyle a}$ de ${\displaystyle M}$ tal que existe ${\displaystyle \varepsilon >0}$ tal que ${\displaystyle B(a,\varepsilon )=\{a\}}$) , então toda aplicação ${\displaystyle f:M\longrightarrow N}$ é contínua no ponto ${\displaystyle a}$. Com efeito, dado ${\displaystyle \varepsilon >0}$, basta tomar ${\displaystyle \delta >0}$ tal que ${\displaystyle B(a,\delta )=\{a\}}$. Assim, ${\displaystyle d(a,x)<\delta \Rightarrow d(f(a),f(x))=0<\varepsilon }$.^[11]
3. Uma aplicação ${\displaystyle f:M\longrightarrow N}$ chama-se uma imersão isométrica quando ${\displaystyle d(x,y)=d(f(x),f(y))}$ para quaisquer ${\displaystyle x,y\in M}$. Neste caso, diz-se também que ${\displaystyle f}$ preserva distâncias.^[12] Note que dado ${\displaystyle \varepsilon >0}$ e ${\displaystyle a\in M}$ qualquer, se ${\displaystyle d(x,a)<\delta }$ com ${\displaystyle \delta =\varepsilon }$ então ${\displaystyle d(f(x),f(a))=d(x,a)<\delta =\varepsilon }$, implicando que ${\displaystyle f}$ é contínua.

Sejam ${\displaystyle M,N}$ espaços métricos. Um homeomorfismo de ${\displaystyle M}$ sobre ${\displaystyle N}$ é uma bijeção contínua ${\displaystyle f:M\longrightarrow N}$ cuja inversa ${\displaystyle f^{-1}:N\rightarrow M}$ também é uma bijeção contínua. Neste caso, diz-se que ${\displaystyle M}$ e ${\displaystyle N}$ são homeomorfos. Ás vezes se usa a expressão "equivalência topológica" em vez de "homeomorfismo". Dois espaços métricos homeomorfos são indistinguíveis do ponto de vista da Topologia. Uma propriedade de que goza um espaço ${\displaystyle M}$ é chamada de uma propriedade topológica quando todo espaço homeomorfo a ${\displaystyle M}$ também goza de tal propriedade. As propriedades topológicas se distinguem das propriedades métricas de ${\displaystyle M}$ que são preservadas pelas isométricas ^[13].

Exemplos:

1. Seja ${\displaystyle M}$ um espaço vetorial normado. Para todo ${\displaystyle a\in M}$ e para todo número real ${\displaystyle \lambda \neq 0}$, a translação ${\displaystyle t_{a}:M\rightarrow M}$ e a homotetia ${\displaystyle m_{\lambda }:M\rightarrow M}$, definidas por ${\displaystyle t_{a}(x)=x+a}$ e ${\displaystyle m_{\lambda }(x)=\lambda \cdot x}$ são homeomorfismos de ${\displaystyle M}$ . De fato, sabemos que ${\displaystyle t_{a}}$ e ${\displaystyle m_{\lambda }}$ são contínuas. Além disso, possuem inversas: ${\displaystyle (t_{a})^{-1}=t_{-a}}$ e ${\displaystyle (m_{\lambda })^{-1}=m_{\mu }}$ (onde ${\displaystyle \mu =1/\lambda }$), as quais também são contínuas.
2. Duas bolas abertas ${\displaystyle B(a;r)}$ e ${\displaystyle B(b;s)}$ em ${\displaystyle M}$ são homeomorfas. Mais precisamente, a composta ${\displaystyle \varphi =t_{b}\circ m_{s/r}\circ t_{-a}}$ define um homeomorfismo ${\displaystyle \varphi :M\rightarrow M}$. Em especial, o homeomorfismo ${\displaystyle \varphi }$ é tal que ${\displaystyle \varphi (B(a;r))=B(b;s)}$.^[14]

Diz-se que sequência ${\displaystyle \{x_{n}\}_{n\in \mathbb {N} }}$ com elementos num espaço métrico ${\displaystyle (X,d)}$ converge para um elemento ${\displaystyle x\in X}$ se para qualquer ${\displaystyle \epsilon >0}$ existe um número natural ${\displaystyle n_{0}=n_{0}(\epsilon )}$ tal que ${\displaystyle d(x,x_{n})<\epsilon }$ para todo ${\displaystyle n\in \mathbb {N} }$ tal que ${\displaystyle n>n_{0}}$. Nessa ocasião, ${\displaystyle x}$ é o único elemento do espaço métrico com esta propriedade, e é chamado de limite da sequência, e escreve-se ${\displaystyle \lim _{n\to +\infty }x_{n}=x}$ ou ${\displaystyle x_{n}\to x}$.

Uma sequência ${\displaystyle \{x_{n}\}_{n\in \mathbb {N} }}$ com elementos num espaço métrico ${\displaystyle (X,d)}$ é de Cauchy ou satisfaz o critério de Cauchy quando para todo ${\displaystyle \epsilon >0}$ pode-se encontrar um número natural ${\displaystyle n_{0}=n_{0}(\epsilon )}$ de modo que ${\displaystyle d(x_{n},x_{m})<\epsilon }$ para quaisquer números naturais ${\displaystyle m,n>n_{0}}$. Pode se mostrar que toda sequência convergente é de Cauchy, e um espaço métrico em que critério de Cauchy é suficiente para convergência é chamado de espaço métrico completo. Exemplos de espaços métricos completos incluem ${\displaystyle \mathbb {R} ,\mathbb {C} ,\mathbb {R} ^{n},\mathbb {C} ^{n}}$ e qualquer Espaço vetorial normado de dimensão finita^[15].

• Lima, Elon Lages (2013). Espaços métricos. Col: Coleção Projeto Euclides 5ª ed. [S.l.]: IMPA. 299 páginas. ISBN 978-85-244-0158-9 

Este artigo sobre matemática é um esboço. Você pode ajudar a Wikipédia expandindo-o. v d e

• Portal da matemática