Estabilidade do sistema solar – Wikipédia, a enciclopédia livre

A estabilidade do sistema solar é um tema de muita investigação em astronomia. Embora os planetas têm sido estáveis historicamente, e ainda serão, a curto prazo, os seus efeitos gravitacionais fracos uns sobre os outros podem acrescentar-se de formas imprevisíveis. Por este motivo (entre outros) o sistema solar é estabelecido como sendo caótico,^[1] e até mesmo os modelos mais precisos de longo prazo para os movimentos orbitais do sistema solar não são válidos durante mais que algumas dezenas de milhões de anos.^[2]

O sistema solar é estável em termos humanos, no que nenhum dos planetas colidem uns com os outros ou serão ejetados do sistema nos próximos bilhões de anos,^[3] e a órbita da Terra irá manter-se relativamente estável.^[4]

Desde a lei de Newton da gravitação (1687), matemáticos e astrônomos (tais como Laplace, Lagrange, Gauss, Poincaré, Kolmogorov, Vladimir Arnold e Jürgen Moser) tem procurado por evidências pela estabilidade do movimentos planetários, e essa busca levou a muitos desenvolvimentos matemáticos, e vários sucessivos "demonstrações" de estabilidade do sistema solar.^[5]

Artigo principal: Problema dos N-Corpos

As órbitas dos planetas estão sujeitas à variações de longo prazo, e a modelagem do sistema solar está sujeita ao problema dos n-corpos.

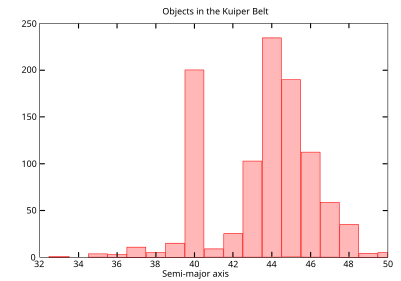
A ressonância acontece quando dois períodos têm uma razão numérica simples. O período mais fundamental para um objeto no Sistema Solar é o seu período orbital e as ressonâncias orbitais permeiam o Sistema Solar. Em 1867, o astrônomo americano Daniel Kirkwood notou que os asteroides no cinturão de asteroides não são distribuídos aleatoriamente.^[6] Havia lacunas distintas no cinturão em locais que correspondiam a ressonância com Júpiter. Por exemplo, não havia asteroides na ressonância 3: 1 - uma distância de 2,5 UA - ou na ressonância 2: 1 em 3,3 UA (UA é a unidade astronômica ou essencialmente a distância do sol à terra) .

Outra forma comum de ressonância no Sistema Solar é a ressonância spin-órbita, em que o período de rotação (o tempo que o planeta ou a lua leva para girar uma vez em torno de seu eixo) tem uma relação numérica simples com seu período orbital. Um exemplo é a nossa Lua, que está em uma ressonância de órbita giratória 1: 1 que mantém o lado mais distante da Lua longe da Terra.

As órbitas dos planetas são caóticas em escalas de tempo mais longas, de tal forma que todo o sistema solar possui um tempo de Lyapunov na faixa de 2–230 milhões de anos.^[3]

Em todos os casos, isso significa que a posição de um planeta ao longo de sua órbita torna-se impossível de prever com alguma certeza (por exemplo, o tempo do inverno e do verão se torna incerto), mas em alguns casos as próprias órbitas podem mudar drasticamente. Esse caos se manifesta mais fortemente como mudanças na excentricidade, com as órbitas de alguns planetas se tornando significativamente mais ou menos elíptica.^[7]

No cálculo, as incógnitas incluem asteróides, o momento quadripolar solar, a perda de massa do Sol por radiação e vento solar e o arrasto do vento solar no planeta magnetosfera, forças das marés galáctica, o efeito fracionário e efeitos da passagem de estrelas.^[8]

Além disso, as equações de movimento descrevem um processo que é inerentemente serial, de modo que há pouco ganho com os maciços paralelos.^{[carece de fontes?]}

Referências