Método de Hartree-Fock – Wikipédia, a enciclopédia livre
Em física computacional e química computacional, o método de Hartree–Fock (HF) é um método aproximativo para determinar a função de onda e a energia de um problema de muitos corpos de um estado estacionário.
O método de Hartree-Fock frequentemente considera que a função de onda de N corpos de um sistema pode ser aproximada por um único determinante de Slater (no caso de muitas partículas serem férmions) ou um permanent (no caso dos bósons) para N orbitais de spins. Utilizando o método variacional, pode-se derivar um conjunto de "N" equações acopladas para "N" orbitais de spins. Uma solução destas equações produz a função de onda de Hartree-Fock e dá a energia do sistema.
Na literatura o método de Hartree-Fock é chamado de método de campo autoconsistente. Ao deduzir o que hoje é chamada de equação de Hartree, como uma solução aproximada da equação de Schrödinger, Douglas Hartree exigiu que o campo final calculado a partir da distribuição de carga fosse autoconsistente com o campo considerado inicialmente. Assim, sua autoconsistência é uma exigência da solução. As soluções para as equações não lineares de Hartree-Fock também se comportam como se cada partícula fosse submetida ao campo médio criado por todas as outras partículas (operador de Hartree-Fock). As equações são universalmente resolvidas por meio de um método iterativo, embora o algoritmo de ponto fixo nem sempre convirja.[1] Este tipo de solução não é a única possível e também não é uma característica essencial do método Hartree-Fock.
O método de Hartree-Fock encontra suas aplicações nas soluções da equação de Schrödinger para átomos, moléculas, nanoestruturas[2] e em sólidos, mas também é usado em física nuclear. (Ver Hartree–Fock–Bogoliubov method para uma discussão da aplicação em física nuclear). Na teoria de estrutura atômica os cálculos devem ser feitos para um espectro de energia com muitos estados excitados. Desse modo o método de Hartree-Fock para átomos considera que a função de onda é uma única função de estado para a configuração atômica, com números quânticos bem definidos e que o nível de energia não é necessariamente o estado fundamental.
Para ambos átomos e moléculas, o método de Hartree-Fock é o ponto de partida para vários métodos de solução que descrevem precisamente o problema de muitos corpos.
O restante deste artigo se concentrará em aplicações da teoria da estrutura eletrônica adequada para moléculas, com o átomo como um caso especial. As discussões aqui são somente restritas ao método de Hartree-Fock, onde o átomo ou a molécula está em uma casca fechada com todos os orbitais (atômicos e molecular) duplamente ocupados. Os sistemas tipo casca aberta, onde alguns dos elétrons não estão emparelhados, podem ser tratados por um dos dois métodos de Hartree-Fock:
- Hartree-Fock de concha aberta restrita Restricted open-shell Hartree–Fock (ROHF)
- Hartree-Fock irrestrito Unrestricted Hartree–Fock (UHF)
Uma breve história
[editar | editar código-fonte]A origem do método de Hartree-Fock data do começo de 1920, logo após a descoberta da Equação de Schrödinger em 1926. Em 1927 Douglas Hartree introduziu o procedimento, que foi chamado de método do campo autoconsistente, para calcular aproximações para função de onda e energia para átomos e íons. Hartree foi guiado por alguns métodos anteriores, semi-empíricos, do início da década de 1920 (por E. Fues, R. B. Lindsay, e ele mesmo) de acordo com a Antiga teoria quântica de Niels Bohr.
No Modelo de Bohr do átomo, a energia do estado com número quântico n é dada em unidades atômicas . Observou-se então, a partir dos espectros atômicos, que os níveis de energia de átomos com muitos elétrons são bem descritos, aplicando uma versão modificada da fórmula de Bohr. Introduzindo o quantum defect d como parâmetro empírico, os níveis de energia de um átomo genérico são dados aproximadamente pela fórmula quantum defect, no sentido de que se pode reproduzir razoavelmente os níveis observados nas regiões de transição Raios X (veja a discussão empírica em Lei de Moseley). A existência de um quantum defect não zero foi atribuído à repulsão elétron elétron, que claramante não existe em um átomo de hidrogênio isolado. Essa repulsão é resultado screening effect da carga nuclear nua. Os primeiros pesquisadores mais tarde introduziram outros potenciais que continham parâmetros empíricos adicionais, com a esperança de reproduzir os dados experimentais.
Hartree procurou acabar com parâmetros empíricos e resolver a equação de Schrödinger independente do tempo de muitos-corpos a partir de princípios físicos fundamentais. Seu primeiro método de solução proposto ficou conhecido como Método de Hartree. Entretanto, muitos dos contemporâneos de Hartree não entenderam o raciocínio físico por trás do Método de Hartree. Para muitos sua conexão com a solução da equação de Schrödinger de muitos-corpos não estava clara. No entanto, em 1928 John C. Slater e J. A. Gaunt mostraram, independentemente, que o método de Hartree poderia ser formulado numa base teórica mais precisa, aplicando o princípio variacional a uma ansatz (função de onda de ensaio) como um produto de funções de partícula única.
Em 1930 Slater e Vladimir Fock, independentemente, apontaram que o método de Hartree não respeitava o princípio de função de onda para partículas idênticas. O método de Hartree usava o princípio de exclusão de Pauli em sua formulação mais velha, proibindo a presença de dois elétrons no mesmo estado quântico. No entanto, este método foi mostrado fundamentalmente incompleto, pois negligenciava a estatística quântica.
Foi então mostrado que um Determinante de Slater, um Determinante de orbitais de partícula única usados pela primeira vez por Heisenberg e Dirac em 1926, satisfez trivialmente as propriedades de Partículas idênticas da solução exata. E Portanto, era adequado usar um ansatz para aplicar o princípio variacional. O método de Hartree original pode então ser visto como uma aproximação ao método de Hartree-Fock negligenciando partículas idênticas. O método original de Fock se baseava fortemente na Teoria dos grupos, e era muito abstrato para os físicos contemporâneos entenderem e implementarem. Em 1935 Hartree reformulou o método para facilitar os cálculos.
O método de Hartree-Fock, apesar de fisicamente mais preciso, foi pouco usado até o advento dos computadores eletrônicos na década de 1950. Isso se deveu às demandas computacionais muito grandes do método Hartree e seus modelos empíricos. Inicialmente, tanto o método Hartree como o método Hartree-Fock foram aplicados exclusivamente a átomos, onde a simetria esférica do sistema permitiu simplificar bastante o problema. Esses métodos aproximados foram (e são) freqüentemente usados em conjunto com a aproximação de campo central, para que os elétrons na mesma casca tenham a mesma parte radial, e para restringir a solução variacional para serem autofunções do spin. Mesmo assim as soluções à mão para as equações de Hartree-Fock de um átomo de tamanho médio eram muito difíceis. E para pequenas moléculas elas requeriam recursos computacionais muito além do que estava disponível antes de 1950.
O algoritimo de Hartree-Fock
[editar | editar código-fonte]O método de Hartree-Fock é tipicamente usado para resolver a equação de Schrödinger independente do tempo para um átomo ou molécula de múltiplos elétrons como descrito na aproximação de Born-Oppenheimer. Como não há soluções conhecidas para sistemas de muitos elétrons (existem soluções para sistemas de um elétron como o átomo de hidrogênio), o problema é resolvido numericamente. Devido a não linearidade introduzida pela aproximação de Hartree-Fock, as equações são resolvidas usando um método não-linear como o de Iteração, que dá origem ao nome método do campo autoconsistente [3].
Aproximações
[editar | editar código-fonte]O método de Hartree-Fock faz cinco simplificações principais, são elas:
- A Aproximação de Born-Oppenheimer é utilizada. A função total da molécula é na verdade uma função das coordenadas de cada um dos núcleos, além da coordenada dos elétrons [3].
- Tipicamente os efeitos da relatividade especial são completamente negligenciados. O operador Momento é tido como não relativístico.
- A solução variacional é uma combinação linear de um número finito de funções de base, que normalmente são (mas nem sempre) escolhidas para serem ortogonais. O conjunto de base finita é assumido como sendo aproximadamente completo.
- Considera-se que cada auto-função da energia é descrita por um único determinante de Slater, um produto antisimétrico da funções de onda do elétron.
- A teoria do campo médio ou aproximação de campo médio, está implícita. Os efeitos decorrentes desses desvios, pressupõe que as correlações dos elétrons são completamente negligenciadas para os elétrons com spins opostos, mas são levados em conta para elétrons com spins paralelos. [4][5] (Electron correlation should not be confused with electron exchange, which is fully accounted for in the Hartree–Fock method.) [3][5]
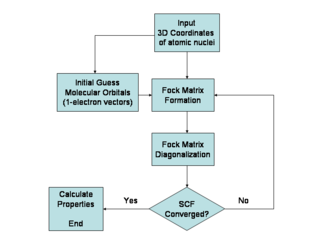
Otimização variacional dos orbitais
[editar | editar código-fonte]O método variacional mostra que para um operador Hamiltoniano independente do tempo, qualquer função de onda irá ter o valor esperado da energia, maior ou igual a energia do verdadeiro estado fundamental, dada pela função de onda do Hamiltonia fornecido. Devido a isso, a energia de Hartree-Fock é superior à verdadeira energia de estado fundamental de uma determinada molécula. No contexto do método de Hartree-Fock, a melhor possibilidade de solução é o Limite de Hartree-Fock, que é o limite em que a energia de Hartree-Fock se aproxima de uma base ortonormal (A outra é a configuração de iteração, onde as duas últimas aproximações do método de Hartree-Fock como descritas acima são desfeitas. Somente quando ambos os limites são alcançados que a solução exata, até a aproximação de Born-Oppenheimer, é obtida.). A energia de Hartree-Fock é a energia mínima de um único determinante de Slater.
O ponto de partida para o método de Hartree-Fock é um conjunto aproximado de funções de onda de um elétron conhecidas como spin-orbital. Para um cálculo orbital atômico, estes são tipicamente os orbitais de um átomo hidrogênio (um átomo com apenas um elétron, mas a carga nuclear apropriada). Para o cálculo do orbital molecular ou cristalino, as funções de onda de um elétron são tipicamente uma combinação linear de orbitais atômicos.
Os orbitais descritos acima apenas representam de maneira mediana a presença dos elétrons. No método de Hartree-Fock, o efeito dos muitos elétrons é contabilizado através da teoria de campo médio. Os orbitais são otimizados, exigindo que eles minimizem a energia do determinante de Slater. As condições variacionais resultantes nos orbitais levam a um novo operador de um elétron, chamado o operador Fock. Os orbitais ocupados são autosoluções do operador Fock, através de transformações unitárias entre si. O operador Fock é um eficiente operador Hamiltoniano de um elétron, sendo a soma de dois termos. O primeiro é uma soma de operadores da energia cinética para cada elétron, energia de repulsão internuclear, e da soma dos termos de atração eletrônica-nuclear Lei de Coulomb. O segundo são os termos Coulombianos de repulsão entre elétrons, descritos através da teoria de campo médio. É então calculada uma energia de repulsão líquida para cada elétron do sistema, tratando todos os elétrons dentro da molécula como uma distribuição suave de carga negativa. Essa é uma simplificação inerente ao método Hartree-Fock, e é equivalente à quinta simplificação da lista acima.
Desde que o operador Fock dependa dos orbitais usados para construir a matriz de Fock, as autofunções do operador Fock são, por sua vez, novos orbitais que podem ser usados para construir um novo operador Fock. Desta forma, os orbitais de Hartree-Fock são otimizados iterativamente até que a mudança na energia eletrônica total caia abaixo de um limiar predefinido. Dessa forma, um conjunto de orbitais autoconsistentes de um elétron são calculados. A função de onda eletrônica de Hartree-Fock é então dada pelo determinante de Slater construído fora destes orbitals. Seguindo os postulados da mecânica quântica, a função de onda de Hartree-Fock pode então ser usada para calcular qualquer propriedade química ou física desejada, dentro da estrutura do método de Hartree-Fock.
Formulação matemática
[editar | editar código-fonte]O operador de Fock
[editar | editar código-fonte]Como o termo de repulsão elétron elétron do Hamiltoniano molecular envolve as coordenadas de dois elétrons diferentes, é necessário reformulá-lo de forma aproximada. Para esta aproximação, todos os termos do Hamiltoniano exato, exceto o termo de repulsão nuclear, são reescritos como a soma dos operadores de um elétron para átomos ou moléculas em uma casca fechada (com dois elétrons em cada orbital).[6] O "(1)" de cada símbolo de operador, indica que o operador é de um único elétron na natureza.
onde
É o operador de Fock para um elétron gerado pelos orbitais ,
É o núcleo do Hamiltoniano de um elétron,
Onde o operador de Coulomb define a energia de repulsão elétron elétron devido a cada um dos dois elétrons j no enésimo orbital.[6]
É o operador de troca, que define a energia de troca dos elétrons devido a antisimetrização da função de onda de todos os n elétrons.[6] Onde o perador "Troca de energia", K, é obtido através do determinante de Slater. Então para encontrar as funções de onda de um elétron pelo método de Hartree-Fock, é equivalente a resolver as equações das autofunções:
Onde são um conjunto de funções de onda um elétron, chamadas de orbitais moleculares de Hartree-Fock.
Combinação linear dos orbitais atômicos
[editar | editar código-fonte]Tipicamente nos cálculos mais modernos do método de Hartree-Fock, as funções de onda para um elétron são uma combinação linear dos orbitais atômicos. Esses orbitais atômicos são chamados orbitais do tipo Slater. Além disso, é muito comum que os "orbitais atômicos" em uso sejam realmente compostos de uma combinação linear de um ou mais orbitais gaussianos, em vez de orbitais do tipo Slater, no interesse de economizar grandes quantidades de tempo de computação.
Diversos conjuntos de bases (química) são usados na prática, a maioria são compostas de funções Gaussianas. Em algumas aplicações, métodos de ortogonalização como o de Gram-Schmidt são usados para produzir um conjunto de bases ortogonais. Isso pode, em princípio, economizar tempo computacional quando o computador está resolvendo as equações de Roothaan Equações de Roothaan-Hall convertendo a matriz de superposição para uma matriz de identidade. No entanto, na maioria dos programas modernos para cálculos Hartree-Fock, este procedimento não é seguido devido ao alto custo numérico da ortogonalização. O advento de algorítmos mais eficientes, muitas vezes escassos, para resolver o problema do autovalor generalizado, como as equações Roothaan-Hall são um exemplo.
Estabilidade numérica
[editar | editar código-fonte]A instabilidade numérica pode ser um problema, e existem algumas maneiras de combater essa instabilidade. Um dos métodos mais simples chama-se F-mixing ou amortecimento. Através do F-mixing, uma vez que uma função de onda de um elétron é calculada, ela não é usada. Em vez disso, é usada uma combinação da função de onda calculada anteriormente para um elétron. Um modo inteligente, usado por Hartrree, para cálculos atômicos era aumentar a carga nuclear unindo então todos os elétrons. E então com o sistema estabilizado, diminúi-se gradualmente a carga do sistema até a carga correta. Para cálculos moleculares, uma abordagem semelhante as vezes é usada primeiro, calcula-se a função de onda para um íon positivo e depois usando esses orbitais como ponto de partida para a molécula neutra. Os programas modernos para o cálculo do método de Hartree-Fock molecular usam uma variedade de métodos para assegurar a convergência das equações de Roothaan-Hall.
Fraquezas, extensões e alternativas
[editar | editar código-fonte]Das cinco simplificações descritas na seção "O algoritmo de Hartree-Fock", a quinta sessão é a mais importante. Uma série de abordagens, coletivamente denominadas métodos pós-Hartree-Fock, foram criadas para incluir a correlação de elétrons com a função de onda de múltiplos elétrons. Uma dessas abordagens, a teoria de perturbação de Moller-Presset, trata a correção como uma perturbação do operador de Fock. Outros autores expandem a função de onda para múltiplos elétrons em termos de uma combinação linear de determinantes de Slater, tais como campo configurável, configuração de iteração, interação quadrática. Ainda outros (Método de Monte Carlo) variam a função de onda de Hartree-Fock multiplicando-a por uma função de correlação (fator de Jastrow), um termo que é explicitamente uma função de múltiplos elétrons que não podem ser decompostas em funções independentes de partícula única.
Referências
- ↑ Froese Fischer, Charlotte (1987). «General Hartree-Fock program». Computer Physics Communication. 43 (3): 355–365. Bibcode:1987CoPhC..43..355F. doi:10.1016/0010-4655(87)90053-1
- ↑ Abdulsattar, Mudar A. (2012). «SiGe superlattice nanocrystal infrared and Raman spectra: A density functional theory study». J. Appl. Phys. 111 (4). 044306 páginas. Bibcode:2012JAP...111d4306A. doi:10.1063/1.3686610
- ↑ a b c Félix, I. M. (2013). «Estudo da estrutura eletrônica do grafeno e grafeno hidratado». UFCG
- ↑ Hinchliffe, Alan (2000). Modelling Molecular Structures 2nd ed. Baffins Lane, Chichester, West Sussex PO19 1UD, England: John Wiley & Sons Ltd. p. 186. ISBN 0-471-48993-X
- ↑ a b Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry. Mineola, New York: Dover Publishing. ISBN 0-486-69186-1
- ↑ a b c Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall. p. 403. ISBN 0-205-12770-3.
Bibliografia
[editar | editar código-fonte]- Levine, Ira N. (1991). Quantum Chemistry 4th ed. Englewood Cliffs, New Jersey: Prentice Hall. pp. 455–544. ISBN 0-205-12770-3
- Cramer, Christopher J. (2002). Essentials of Computational Chemistry. Chichester: John Wiley & Sons, Ltd. pp. 153–189. ISBN 0-471-48552-7
- Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry. Mineola, New York: Dover Publishing. ISBN 0-486-69186-1
Ligações externas
[editar | editar código-fonte]- Introduction by C. David Sherrill
- Mean-Field Theory: Hartree-Fock and BCS in E. Pavarini, E. Koch, J. van den Brink, and G. Sawatzky: Quantum materials: Experiments and Theory, Jülich 2016, ISBN 978-3-95806-159-0


 French
French Deutsch
Deutsch
={\hat {H}}^{\text{core}}(1)+\sum _{j=1}^{N/2}[2{\hat {J}}_{j}(1)-{\hat {K}}_{j}(1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d3e0a1ce3b1b528f799d01f7eda355f71f12e5c)
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32f43980de090a8055a1bd5b601945b2316d583f)





