Momento de dipolo magnético anômalo – Wikipédia, a enciclopédia livre

A tradução deste artigo está abaixo da qualidade média aceitável. Talvez tenha sido feita por um tradutor automático ou alguém que não conhece bem o português ou a língua original. Caso queira colaborar com a Wikipédia, consulte a versão anglófona e melhore este verbete conforme o guia de tradução. (Maio de 2023)

Na eletrodinâmica quântica, o momento magnético anômalo de uma partícula é uma contribuição dos efeitos da mecânica quântica, expressos pelos diagramas de Feynman com loops, ao momento magnético dessa partícula. (O momento magnético, também chamado de momento de dipolo magnético, é uma medida da força de uma fonte magnética.)

O momento magnético de "Dirac", correspondente aos diagramas de Feynman em nível de árvore (que pode ser pensado como o resultado clássico), pode ser calculado a partir da equação de Dirac. Geralmente é expresso em termos do fator-g; a equação de Dirac prevê ${\displaystyle g=2}$. Para partículas como o elétron, esse resultado clássico difere do valor observado por uma pequena fração de um por cento. A diferença é o momento magnético anômalo, denotado por ${\displaystyle a}$ e definido como $${\displaystyle a={\frac {g-2}{2}}}$$

A contribuição de um loop para o momento magnético anômalo - correspondente à primeira e maior correção da mecânica quântica - do elétron é encontrada calculando a função de vértice mostrada no diagrama adjacente. O cálculo é relativamente simples ^[1] e o resultado de um loop é:

$${\displaystyle a_{\text{e}}={\frac {\alpha }{2\pi }}\approx 0.001\,161\,4,}$$

onde ${\displaystyle \alpha }$ é a constante de estrutura fina. Este resultado foi encontrado pela primeira vez por Julian Schwinger em 1948 ^[2] e está gravado em sua lápide. Em 2016, os coeficientes da fórmula da EDQ para o momento magnético anômalo do elétron são conhecidos analiticamente até ${\displaystyle \alpha ^{3}}$ ^[3] e foram calculados até a ordem ${\displaystyle \alpha ^{5}}$:^[4][5][6]

$${\displaystyle a_{\text{e}}=0.001\,159\,652\,181\,643(764)}$$

A previsão da EDQ concorda com o valor medido experimentalmente em mais de 10 algarismos significativos, tornando o momento magnético do elétron a previsão verificada com maior precisão na história da física. (Consulte os testes de precisão da EDQ para obter detalhes.) O valor experimental atual e a incerteza são:^[7] $${\displaystyle a_{\text{e}}=0.001\,159\,652\,180\,73(28)}$$

De acordo com este valor, ${\displaystyle a_{\text{e}}}$ é conhecido com uma precisão de cerca de 1 parte em 1 bilhão (10⁹). Isso exigiu medir ${\displaystyle g}$ com uma precisão de cerca de 1 parte em 1 trilhão (10¹²).

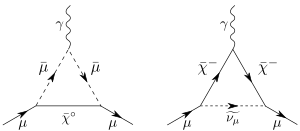
O momento magnético anômalo do múon é calculado de maneira semelhante ao do elétron. A previsão do valor do momento magnético anômalo do múon inclui três partes:^[8] $${\displaystyle {\begin{aligned}a_{\mu }^{\mathrm {SM} }&=a_{\mu }^{\mathrm {QED} }+a_{\mu }^{\mathrm {EW} }+a_{\mu }^{\mathrm {hadron} }\\&=0.001\,165\,918\,04(51)\end{aligned}}}$$

Dos dois primeiros componentes, ${\displaystyle a_{\mu }^{\mathrm {QED} }}$ representa os loops de fótons e léptons e ${\displaystyle a_{\mu }^{\mathrm {EW} }}$ os loops dos bóson W, bóson de Higgs e bóson Z; ambos os componentes podem ser calculados precisamente a partir de primeiros princípios. O terceiro termo, ${\displaystyle a_{\mu }^{\mathrm {hadron} }}$, representa loops de hádrons; ele não pode ser calculado com precisão apenas a partir da teoria. Seu valor é estimado a partir de medições experimentais da razão entre as seções de choque hadrônica e muônica (R) em colisões elétron-antielétron (e⁻–e⁺). Em julho de 2017, observou-se que a medição discorda do Modelo Padrão em 3,5 desvios padrão,^[9] sugerindo que a física além do Modelo Padrão pode estar tendo um efeito (ou que os erros teóricos/experimentais não estão completamente sob controle). Esta é uma das discrepâncias de longa data entre o Modelo Padrão e os experimentos.

O experimento E821 no Brookhaven National Laboratory (BNL) estudou a precessão de múon e antimúon em um campo magnético externo constante enquanto circulavam em um anel de armazenamento confinante.^[10] O experimento E821 relatou o seguinte valor médio:^[8] $${\displaystyle a_{\mu }=0.001\;165\;920\;9(6).}$$

Um novo experimento no Fermilab chamado "Muon g−2" usando o ímã do E821 irá melhorar a precisão deste valor.^[11] A coleta de dados começou em março de 2018 e deve terminar em setembro de 2022.^[12] Um resultado provisório divulgado em 7 de abril de 2021^[13] rende ${\displaystyle a_{\mu }=0.001\,165\,920\,40(54)}$ que, em combinação com as medições existentes, fornece uma estimativa mais precisa ${\displaystyle a_{\mu }=0.001\,165\,920\,61(41)}$ , excedendo a previsão do Modelo Padrão em 4,2 desvios padrão. Além disso, o experimento E34 no J-PARC planeja iniciar sua primeira tomada de dados em 2024.^[14]

Em abril de 2021, um grupo internacional de quatorze físicos relatou que, usando simulações ab-initio de cromodinâmica quântica e eletrodinâmica quântica, eles conseguiram obter uma aproximação baseada em teoria concordando mais com o valor experimental do que com o valor baseado em teoria anterior que se fundamentava em experimentos de aniquilação elétron-pósitron.^[15][16]

A previsão do Modelo Padrão para o momento de dipolo magnético anômalo do tau é de:^[17] $${\displaystyle a_{\tau }=0.001\,177\,21(5),}$$ enquanto o melhor limite medido para ${\displaystyle a_{\tau }}$ é:^[18]

$${\displaystyle -0.052<a_{\tau }<+0.013.}$$

As partículas compostas geralmente têm um momento magnético anômalo enorme. Os núcleons (prótons e nêutrons, ambos compostos de quarks) são exemplos. Os momentos magnéticos dos núcleons são muito grandes e foram inesperados; o momento magnético do próton é grande demais para uma partícula elementar, enquanto não se esperava que o nêutron, que não tem carga, tivesse um momento magnético.

• Sergei Vonsovsky (1975). Magnetism of Elementary Particles. [S.l.]: Mir Publishers 

O Commons possui uma categoria com imagens e outros ficheiros sobre Momento de dipolo magnético anômalo

• Overview of the g−2 experiment
• Kusch, P.; Foley, H. M. (1948). «The Magnetic Moment of the Electron». Physical Review. 74 (3): 250–263. Bibcode:1948PhRv...74..250K. doi:10.1103/PhysRev.74.250 
• Aoyama, T.; et al. (2020). «The anomalous magnetic moment of the muon in the Standard Model». Physics Reports. 887: 1–166. Bibcode:2020PhR...887....1A. arXiv:2006.04822. doi:10.1016/j.physrep.2020.07.006