Teoria algébrica dos grafos – Wikipédia, a enciclopédia livre

A teoria algébrica dos grafos é um ramo da matemática em que os métodos algébricos são aplicados a problemas sobre grafos. Isso contrasta com as abordagens geométricas, combinatórias ou algorítmicas . Existem três ramos principais da teoria de grafos algébricos, envolvendo o uso de álgebra linear, o uso de teoria de grupos e o estudo de grafos invariantes.

O primeiro ramo da teoria algébrica de grafos envolve o estudo de grafos em conexão com álgebra linear . Especialmente, estuda o espectro da matriz de adjacência, ou a matriz laplaciana de um gráfico (essa parte da teoria algébrica dos grafos também é chamada de teoria espectral dos grafos). Para o gráfico de Petersen, por exemplo, o espectro da matriz de adjacência é (−2,   -2,   -2,   -2,   1   1   1   1   1   3) Vários teoremas relacionam propriedades do espectro a outras propriedades gráficas . Como um exemplo simples, um gráfico conectado com diâmetro D terá pelo menos D +1 valores distintos em seu espectro. ^[1] Aspectos dos espectros de gráficos têm sido utilizados na análise da sincronização das redes de internet.

O segundo ramo da teoria algébrica de grafos envolve o estudo de gráficos em conexão com a teoria de grupos, particularmente grupos de automorfismo e teoria de grupos geométricos. O foco é colocado em várias famílias de gráficos baseados em simetria (como gráficos simétricos, gráficos transitivos em vértices, gráficos transitivos em arestas, gráficos transitivos a distância, gráficos transitivos a distância, gráficos regulares a distância e gráficos fortemente regulares) e nas relações de inclusão entre essas famílias. Algumas dessas categorias de gráficos são escassas o suficiente para que listas de gráficos possam ser elaboradas. Pelo teorema de Frucht, todos os grupos podem ser representados como o grupo automorfismo de um gráfico conectado (de fato, de um gráfico cúbico). ^[2] Outra conexão com a teoria de grupos é que, a partir de qualquer grupo, podem ser gerados grafos simétricos conhecidos como grafo de Cayley, os quais possuem propriedades relacionadas à estrutura do grupo. ^[1]

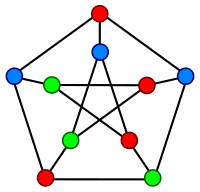
Este segundo ramo da teoria algébrica dos grafos está relacionado ao primeiro, uma vez que as propriedades de simetria de um gráfico são refletidas em seu espectro. Em particular, o espectro de um gráfico altamente simétrico, como o gráfico de Petersen, possui poucos valores distintos ^[1] (o gráfico de Petersen possui 3, que é o mínimo possível, dado seu diâmetro). Para grafos de Cayley, o espectro pode ser relacionado diretamente à estrutura do grupo, em particular aos seus caracteres irredutíveis. ^[3]

Finalmente, o terceiro ramo da teoria algébrica dos grafos diz respeito às propriedades algébricas dos invariantes de grafos e, especialmente, do polinômio cromático, do polinômio de Tutte e dos invariantes de nó. O polinômio cromático de um grafo, por exemplo, conta o número de suas cores de vértice apropriadas. Para o gráfico de Petersen, esse polinômio é ${\displaystyle t(t-1)(t-2)(t^{7}-12t^{6}+67t^{5}-230t^{4}+529t^{3}-814t^{2}+775t-352)}$ . ^[1] Em particular, isso significa que o gráfico Petersen não pode ser adequadamente colorido com uma ou duas cores, mas pode ser colorido de 120 maneiras diferentes com três cores. Muito trabalho nessa área da teoria dos grafos algébricos foi motivado por tentativas de provar o teorema das quatro cores . No entanto, ainda existem muitos problemas em aberto, como caracterizar gráficos que possuem o mesmo polinômio cromático e determinar quais polinômios são cromáticos.

• Teoria dos grafos espectrais
• Combinatória algébrica
• Conectividade algébrica
• Decomposição de Dulmage-Mendelsohn
• Propriedade do grafo
• Matriz de adjacência

Referências

• Media relacionados com Teoria algébrica dos grafos no Wikimedia Commons