Compus de trei octaedre

Compus de trei octaedre
Descriere
Tipcompus poliedric uniform
Fețe24 triunghiuri echilaterale
Laturi (muchii)36
Vârfuri18
Grup de simetrie
  • Compus: octaedrică (Oh), de ordinul 48
  • Constituenți: octaedrică (Oh), de ordinul 48
Poliedru dualcompus de trei cuburi
ProprietățiConstituenți: 3 octaedre regulate
Figura vârfului

Compusul de trei octaedre este un compus poliedric, format din trei octaedre regulate, având același centru, dar rotite unul față de altul. Deși a apărut mai devreme în literatura matematică, a fost redescoperit și popularizat de M. C. Escher, care a folosit-o în imaginea centrală a litografiei Stars din 1948.

Construcție

[modificare | modificare sursă]

Un octaedru regulat poate fi circumscris în jurul unui cub în așa fel încât cele opt laturi din două pătrate opuse ale cubului să se afle pe cele opt fețe ale octaedrului. Cele trei octaedre formate în acest fel din cele trei perechi de pătrate opuse din cuburi formează compusul de trei octaedre.[1] Cele opt vârfuri ale cubului sunt aceleași cu cele opt puncte din compus unde se intersectează câte trei laturi.[2] Fiecare dintre laturile octaedrului care participă la aceste triple intersecții este divizată în punctul de intersecție în raportul 1:√2.[2] Restul laturilor octaedrului se intersectează în perechi, în interiorul compusului; intersecțiile lor sunt în mijlocul lor și formează unghiuri drepte.

Compusul de trei octaedre poate fi format și din trei copii ale unui singur octaedru prin rotirea fiecărei copii cu un unghi de π/4 în jurul uneia dintre cele trei axe de simetrie care trec prin două vârfuri opuse ale octaedrului inițial.[3] O a treia construcție pentru același compus de trei octaedre este ca poliedru dual al compusului de trei cuburi, unul dintre compușii poliedrici uniformi.

Cele șase vârfuri ale unuia dintre cele trei octaedre au coordonatele (0, 0, ±2) și (±√2, ±√2 , 0). Celelalte două octaedre au coordonate care pot fi obținute din aceste coordonate prin interschimbarea coordonatei z cu coordonatele x sau y.[1][2]

Simetrii

[modificare | modificare sursă]
Dodecaedru rombic stelat, un compus din trei octaedre aplatizate utilizat în Studiu pentru Stele⁠(d) și Cascada⁠(d) ale lui M. C. Escher

Compusul de trei octaedre are același grup de simetrie ca un singur octaedru. Este un deltaedru izoedric, ceea ce înseamnă că fețele sale sunt triunghiuri echilaterale și că are o simetrie care aplică orice față pe orice altă față. Există o familie infinită cunoscută de deltaedre izoedrice și încă 36 care nu se încadrează în această familie; compusul de trei octaedre este unul dintre cele 36 de exemple separate.[4] Însă grupul său de simetrie nu aplică orice vârf pe orice alt vârf, deci nu este un compus poliedric uniform.

Intersecția celor trei octaedre este un poliedru convex cu 14 vârfuri și 24 de fețe, un hexaedru tetrakis, format prin atașarea unei piramide pătrate joase pe fiecare față a cubului central.[2] Astfel, compusul poate fi considerat o stelare a hexaedrului tetrakis. O formă diferită a hexaedrului tetrakis, formată prin utilizarea piramidelor mai înalte pe fiecare față a cubului este neconvexă, dar are fețe triunghiulare echilaterale care se află în aceleași plane cu fețele celor trei octaedre; este alt poliedru dintre deltaedrele izoedrice cunoscute. Un al treilea deltaedru izoedric care are aceleași plane ale fețelor, compusul de șase tetraedre, poate fi format prin stelarea fiecărei fețe a compusului de trei octaedre pentru a forma trei stellae octangulae. Un al patrulea deltaedru izoedric cu aceleași plane ale fețelor este o stelare a compusului de trei octaedre, are aceeași structură combinatorică cu hexaedrul tetrakis, dar cu fețele cubului adâncite spre interior în piramide care se intersectează, față de piramidele atașate la exteriorul cubului.[4]

Cubul în jurul căruia pot fi circumscrise cele trei octaedre are nouă plane de simetrie de reflexie. Trei dintre aceste plane de reflexie trec paralel cu laturile cubului, la jumătatea distanței dintre două laturi opuse; celelalte șase trec în diagonală prin cub, prin patru dintre vârfurile acestuia. Aceste nouă plane coincid cu cele nouă plane ecuatoriale ale celor trei octaedre.[2]

Istoric

[modificare | modificare sursă]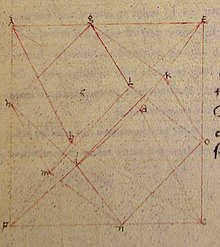
Octaedru circumscris unui cub, desenat de Piero della Francesca în cartea sa De quinque corporibus regularibus

În manuscrisul din secolul al XV-lea De quinque corporibus regularibus de Piero della Francesca, acesta include un desen al unui octaedru circumscris unui cub, cu opt laturi ale cubului situate pe cele opt fețe ale octaedrului. Trei octaedre circumscrise în acest fel în jurul unui singur cub ar forma compusul de trei octaedre, dar della Francesca nu descrie acest compus.[5]

Următoarea apariție a compusului de trei octaedre în literatura matematică pare a fi o lucrare din 1900 a lui Max Brückner, care îl menționează și include o fotografie a unui model al acestuia.[2][6]

Artistul olandez M. C. Escher, în litografia sa din 1948, Stele, a folosit ca figură centrală o cușcă de această formă, care conține doi cameleoni plutind în spațiu.[7] Coxeter, presupunând că Escher a redescoperit această formă în mod independent, scrie că „Este remarcabil că Escher, fără nicio cunoștință de algebră sau geometrie analitică, a fost capabil să redescopere această figură extrem de simetrică".[2] Însă George W. Hart a arătat că Escher cunoștea lucrarea lui Brückner, pe care a folosit-o la mai multe poliedre stelate și compuși poliedrici pe care i-a desenat.[8] La începutul anului 1948 Escher făcuse o litografie preliminară cu o temă similară, „Studiu pentru Stele”, dar în loc să folosească în studiu compusul de trei octaedre, a folosit o formă diferită, dar înrudită, un dodecaedru rombic stelat (numit uneori poliedrul lui Escher), care poate fi format ca un compus de trei octaedre aplatizare.[9] Această formă ca poliedru este identică din punct de vedere topologic cu dodecaedrul disdyakis, care poate fi considerat un dodecaedru rombic cu piramide mai scurte pe fețele rombice. Figura dublă a compusului octaedric, compusul din trei cuburi, este de asemenea prezentată într-o litografie de Escher ulterioară, Cascada, lângă același dodecaedru rombic stelat.[7]

Compusul de trei octaedre a reapărut în literatura matematică în lucrarea lui Bakos & Johnson (1959), care i-a observat existența și a furnizat coordonatele vârfurilor sale. A fost studiat mai în detaliu de Wenninger (1968) și Coxeter (1985).

Note

[modificare | modificare sursă]
  1. ^ a b en Bakos, T.; Johnson, Norman W. (), „Octahedra inscribed in a cube”, The Mathematical Gazette, 43 (343): 17–20, JSTOR 3608867 
  2. ^ a b c d e f g en Coxeter, H. S. M. (), „A special book review: M. C. Escher: His life and complete graphic work”, The Mathematical Intelligencer, 7 (1): 59–69, doi:10.1007/BF03023010 
  3. ^ en Wenninger, Magnus J. (), „Some interesting octahedral compounds”, The Mathematical Gazette, 52 (379): 16–23, JSTOR 3614454 
  4. ^ a b en Shephard, G. C. (), „Isohedral deltahedra”, Periodica Mathematica Hungarica, 39 (1–3): 83–106, doi:10.1023/A:1004838806529 .
  5. ^ en Hart, George W. (), „Piero della Francesca's Polyhedra”, Virtual Polyhedra .
  6. ^ de Brückner, Max (), Vielecke und Vielflache, Leipzig: Teubner, p. 188 and Tafel VIII 12 . As cited by Coxeter (1985)
  7. ^ a b en Hart, George W. (), „The Polyhedra of M.C. Escher”, Virtual Polyhedra 
  8. ^ en Hart, George W., „Max Brücknerʼs Wunderkammer of Paper Polyhedra”, Bridges 2019 Conference Proceedings (PDF), pp. 59–66 
  9. ^ en The compound of three octahedra and a remarkable compound of three square dipyramids, the Escher's solid, Livio Zefiro, University of Genova.

Legături externe

[modificare | modificare sursă]
Portal icon Portal Matematică
Adus de la https://ro.wikipedia.org/w/index.php?title=Compus_de_trei_octaedre&oldid=15917612