Fagure dodecaedric rombic

Fagure dodecaedric rombic
Tip	dual al unui fagure uniform, convex
Diagramă Coxeter	=
Celule	V3.4.3.4
Fețe	romburi
Grup Coxeter	½${\displaystyle {\tilde {C}}_{3}}$, [1+,4,3,4] ${\displaystyle {\tilde {B}}_{3}}$, [4,31,1] ${\displaystyle {\tilde {A}}_{3}}$×2, <[3[4]]>
Grup de simetrie	Fm3m (225)
Dual	Fagure tetraedric-octaedric
Proprietăți	Fagure convex, tranzitiv pe celule, fețe și laturi

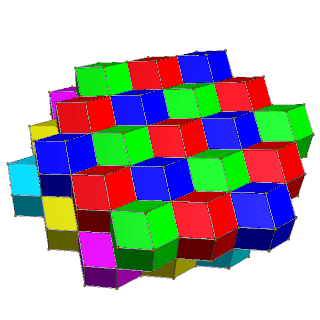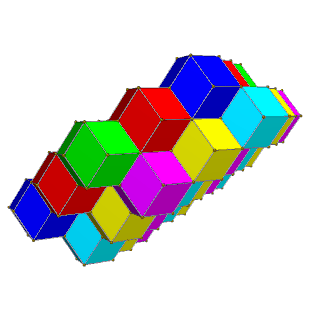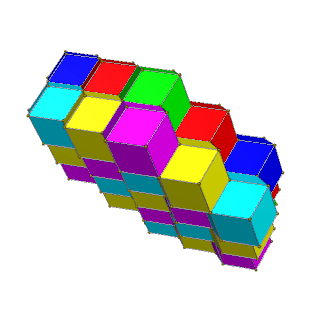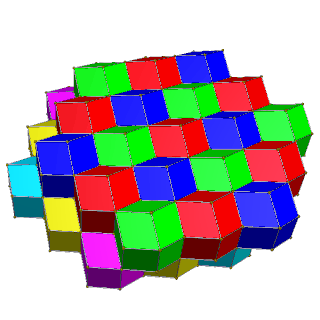
Un fagure dodecaedric rombic este o teselare (sau fagure) a spațiului euclidian tridimensional. Este diagrama Voronoi^⁠(d) a împachetării sferelor^⁠(d) într-o rețea cubică cu fețe centrate, care are cea mai densă împachetare posibilă de sfere egale în spațiul obișnuit (v. Conjectura Kepler^⁠(d)).^[1]

Este format din copii ale unui singur tip de celule, dodecaedrul rombic. Toate fețele sunt romburi cu diagonalele în raportul 1:√2. Pe fiecare latură se întâlnesc câte trei celule. Prin urmare este tranzitiv pe celule, fețe și laturi, dar nu și pe vârfuri, având două tipuri de vârfuri. În vârfurile unde se întâlnesc unghiurile obtuze ale fețelor rombice se întâlnesc câte 4 celule, iar în vârfurile unde se întâlnesc unghiurile ascuțite ale fețelor rombice se întâlnesc câte 6 celule.

Dodecaedrul rombic poate fi răsucit pe una dintre secțiunile sale transversale hexagonale pentru a forma un dodecaedru trapezo-rombic, care este celula unei teselări oarecum asemănătoare, diagrama Voronoi a împachetării compacte a sferelor^⁠(d).

Fagurele poate fi derivat dintr-o teselare cubică alternată prin augmentarea fiecărei fețe a fiecărui cub cu o piramidă

Vedere din interiorul fagurelui dodecaedric rombic

Celule pot fi colorate cu 4 culori în straturi pătrate de câte 2 culori, unde celulele învecinate au culori diferite, sau cu 6 culori în straturi hexagonale de câte 3 culori, unde celulele de aceeași culoare nu au niciun contact.

4 culori	6 culori
Alternează straturile pătrate de celule galbene și albastre, cu cele de celule roșii și verzi	Alternează straturile hexagonale de celule roșii, verzi și albastre, cu cele de celule violete, azurii și galbene

Fagurele dodecaedric rombic poate fi divizat într-un fagure trapezoedric trigonal cu fiecare dodecaedru rombic divizat în 4 trapezoedre trigonale. Fiecare dodecaedru rombic poate fi de asemenea divizat față de punctul central în 12 piramide rombice ale fagurelui piramidal rombic.

• Materiale media legate de fagure dodecaedric rombic la Wikimedia Commons
• en Eric W. Weisstein, Space-filling polyhedron la MathWorld.
• en Examples of Housing Construction using this geometry

Portal Matematică

v • d • m Faguri convecși regulați și uniformi în dimensiunile 2–8
Spațiu	Familia	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E2	Pavare uniformă	{3[3]}	δ3	hδ3	qδ3	Hexagonală
E3	Fagure convex uniform	{3[4]}	δ4	hδ4	qδ4
E4	4-fagure uniform	{3[5]}	δ5	hδ5	qδ5	Fagure 24-celule
E5	5-fagure uniform	{3[6]}	δ6	hδ6	qδ6
E6	6-fagure uniform	{3[7]}	δ7	hδ7	qδ7	222
E7	7-fagure uniform	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	8-fagure uniform	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
En-1	(n−1)-fagure uniform	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21