În matematică , funcțiile Kelvin , notate Berν (x ) și Beiν (x ), sunt partea reală și respectiv partea imaginară a funcției:
J ν ( x e 3 π i / 4 ) {\displaystyle J_{\nu }(xe^{3\pi i/4})\,\!} unde x este real, iar J ν ( z ) {\displaystyle J_{\nu }(z)\,\!} funcția Bessel de prima speță și de ordinul ν.
Similar, funcțiile Kerν (x ) și Keiν (x ) sunt respectiv partea reală si partea imaginară a funcției:
K ν ( x e 3 π i / 4 ) {\displaystyle K_{\nu }(xe^{3\pi i/4})\,\!} unde K ν ( z ) {\displaystyle K_{\nu }(z)\,} funcția Bessel modificată de speța a II-a și de ordinul ν.
Deși funcțiile Kelvin sunt definite ca parte reală si imaginară ale funcțiilor Bessel cu x real, ele pot fi prelungite analitic pentru argumente complexe x e i φn x ) și Bein x ) pentru n întreg, funcțiile Kelvin au un punct de ramificație în x = 0.
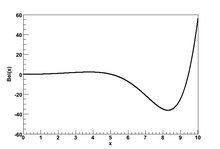
Ber(x) pentru x {\displaystyle x} B e r ( x ) / e x / 2 {\displaystyle \mathrm {Ber} (x)/e^{x/{\sqrt {2}}}} x {\displaystyle x} Pentru n întreg, Bern x ) are următoarea dezvoltare în serie:
B e r n ( x ) = ( x 2 ) n ∑ k ≥ 0 cos [ ( 3 n 4 + k 2 ) π ] k ! Γ ( n + k + 1 ) ( x 2 4 ) k {\displaystyle \mathrm {Ber} _{n}(x)=\left({\frac {x}{2}}\right)^{n}\sum _{k\geq 0}{\frac {\cos \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]}{k!\Gamma (n+k+1)}}\left({\frac {x^{2}}{4}}\right)^{k}} unde Γ ( z ) {\displaystyle \Gamma (z)} funcția Gamma .
Cazul special Ber 0 ( x ) {\displaystyle _{0}(x)} ( x ) {\displaystyle (x)}
B e r ( x ) = 1 + ∑ k ≥ 1 ( − 1 ) k ( x / 2 ) 4 k [ ( 2 k ) ! ] 2 {\displaystyle \mathrm {Ber} (x)=1+\sum _{k\geq 1}{\frac {(-1)^{k}(x/2)^{4k}}{[(2k)!]^{2}}}} iar dezvoltarea asimptotică este
B e r ( x ) ∼ e x 2 2 π x [ f 1 ( x ) cos α + g 1 ( x ) sin α ] − K e i ( x ) π {\displaystyle \mathrm {Ber} (x)\sim {\frac {e^{\frac {x}{\sqrt {2}}}}{\sqrt {2\pi x}}}[f_{1}(x)\cos \alpha +g_{1}(x)\sin \alpha ]-{\frac {\mathrm {Kei} (x)}{\pi }}} unde α = x / 2 − π / 8 {\displaystyle \alpha =x/{\sqrt {2}}-\pi /8}
f 1 ( x ) = 1 + ∑ k ≥ 1 cos ( k π / 4 ) k ! ( 8 x ) k ∏ l = 1 k ( 2 l − 1 ) 2 {\displaystyle f_{1}(x)=1+\sum _{k\geq 1}{\frac {\cos(k\pi /4)}{k!(8x)^{k}}}\prod _{l=1}^{k}(2l-1)^{2}} g 1 ( x ) = ∑ k ≥ 1 sin ( k π / 4 ) k ! ( 8 x ) k ∏ l = 1 k ( 2 l − 1 ) 2 {\displaystyle g_{1}(x)=\sum _{k\geq 1}{\frac {\sin(k\pi /4)}{k!(8x)^{k}}}\prod _{l=1}^{k}(2l-1)^{2}}
Bei(x) pentru x {\displaystyle x} B e i ( x ) / e x / 2 {\displaystyle \mathrm {Bei} (x)/e^{x/{\sqrt {2}}}} x {\displaystyle x} pentru n {\displaystyle n} n ( x ) {\displaystyle _{n}(x)}
B e i n ( x ) = ( x 2 ) n ∑ k ≥ 0 sin [ ( 3 n 4 + k 2 ) π ] k ! Γ ( n + k + 1 ) ( x 2 4 ) k {\displaystyle \mathrm {Bei} _{n}(x)=\left({\frac {x}{2}}\right)^{n}\sum _{k\geq 0}{\frac {\sin \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]}{k!\Gamma (n+k+1)}}\left({\frac {x^{2}}{4}}\right)^{k}} unde Γ ( z ) {\displaystyle \Gamma (z)} funcția Gamma . Cazul special Bei 0 ( x ) {\displaystyle _{0}(x)} ( x ) {\displaystyle (x)}
B e i ( x ) = ∑ k ≥ 0 ( − 1 ) k ( x / 2 ) 4 k + 2 [ ( 2 k + 1 ) ! ] 2 {\displaystyle \mathrm {Bei} (x)=\sum _{k\geq 0}{\frac {(-1)^{k}(x/2)^{4k+2}}{[(2k+1)!]^{2}}}} iar dezvoltarea asimptotică este:
B e i ( x ) ∼ e x 2 2 π x [ f 1 ( x ) sin α + g 1 ( x ) cos α ] − K e r ( x ) π {\displaystyle \mathrm {Bei} (x)\sim {\frac {e^{\frac {x}{\sqrt {2}}}}{\sqrt {2\pi x}}}[f_{1}(x)\sin \alpha +g_{1}(x)\cos \alpha ]-{\frac {\mathrm {Ker} (x)}{\pi }}} unde α {\displaystyle \alpha } f 1 ( x ) {\displaystyle f_{1}(x)} g 1 ( x ) {\displaystyle g_{1}(x)} ( x ) {\displaystyle (x)}
Pentru n întreg, Kern x ) are următoarea dezvoltare în serie:
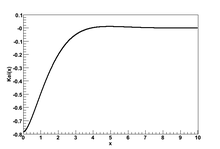
K e r n ( x ) = 1 2 ( x 2 ) − n ∑ k = 0 n − 1 cos [ ( 3 n 4 + k 2 ) π ] ( n − k − 1 ) ! k ! ( x 2 4 ) k + 1 2 ( x 2 ) n ∑ k ≥ 0 cos [ ( 3 n 4 + k 2 ) π ] ψ ( k + 1 ) + ψ ( n + k + 1 ) k ! ( n + k ) ! ( x 2 4 ) k − ln ( x 2 ) B e r n ( x ) + π 4 B e i n ( x ) {\displaystyle {\begin{aligned}\mathrm {Ker} _{n}(x)&={\frac {1}{2}}\left({\frac {x}{2}}\right)^{-n}\sum _{k=0}^{n-1}\cos \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]{\frac {(n-k-1)!}{k!}}\left({\frac {x^{2}}{4}}\right)^{k}\\&+{\frac {1}{2}}\left({\frac {x}{2}}\right)^{n}\sum _{k\geq 0}\cos \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]{\frac {\psi (k+1)+\psi (n+k+1)}{k!(n+k)!}}\left({\frac {x^{2}}{4}}\right)^{k}\\&-\ln \left({\frac {x}{2}}\right)\mathrm {Ber} _{n}(x)+{\frac {\pi }{4}}\mathrm {Bei} _{n}(x)\end{aligned}}} Ker(x) pentru x {\displaystyle x} K e r ( x ) e x / 2 {\displaystyle \mathrm {Ker} (x)e^{x/{\sqrt {2}}}} x {\displaystyle x} unde ψ ( z ) {\displaystyle \psi (z)} funcția Digamma .
Cazul special Ker 0 ( x ) {\displaystyle _{0}(x)} ( x ) {\displaystyle (x)}
K e r ( x ) = − ln ( x 2 ) B e r ( x ) + π 4 B e i ( x ) + ∑ k ≥ 0 ( − 1 ) k ψ ( 2 k + 1 ) [ ( 2 k ) ! ] 2 ( x 2 4 ) 2 k {\displaystyle \mathrm {Ker} (x)=-\ln \left({\frac {x}{2}}\right)\mathrm {Ber} (x)+{\frac {\pi }{4}}\mathrm {Bei} (x)+\sum _{k\geq 0}(-1)^{k}{\frac {\psi (2k+1)}{[(2k)!]^{2}}}\left({\frac {x^{2}}{4}}\right)^{2k}} și dezvoltarea asimptotică:
K e r ( x ) ∼ π 2 x e − x 2 [ f 2 ( x ) cos β + g 2 ( x ) sin β ] , {\displaystyle \mathrm {Ker} (x)\sim {\sqrt {\frac {\pi }{2x}}}e^{-{\frac {x}{\sqrt {2}}}}[f_{2}(x)\cos \beta +g_{2}(x)\sin \beta ],} unde β = x / 2 + π / 8 {\displaystyle \beta =x/{\sqrt {2}}+\pi /8}
f 2 ( x ) = 1 + ∑ k ≥ 1 ( − 1 ) k cos ( k π / 4 ) k ! ( 8 x ) k ∏ l = 1 k ( 2 l − 1 ) 2 {\displaystyle f_{2}(x)=1+\sum _{k\geq 1}(-1)^{k}{\frac {\cos(k\pi /4)}{k!(8x)^{k}}}\prod _{l=1}^{k}(2l-1)^{2}} g 2 ( x ) = ∑ k ≥ 1 ( − 1 ) k sin ( k π / 4 ) k ! ( 8 x ) k ∏ l = 1 k ( 2 l − 1 ) 2 . {\displaystyle g_{2}(x)=\sum _{k\geq 1}(-1)^{k}{\frac {\sin(k\pi /4)}{k!(8x)^{k}}}\prod _{l=1}^{k}(2l-1)^{2}.}
Pentru n întreg, Kein x ) are dezvoltarea in serie:
K e i n ( x ) = 1 2 ( x 2 ) − n ∑ k = 0 n − 1 sin [ ( 3 n 4 + k 2 ) π ] ( n − k − 1 ) ! k ! ( x 2 4 ) k + 1 2 ( x 2 ) n ∑ k ≥ 0 sin [ ( 3 n 4 + k 2 ) π ] ψ ( k + 1 ) + ψ ( n + k + 1 ) k ! ( n + k ) ! ( x 2 4 ) k − ln ( x 2 ) B e i n ( x ) − π 4 B e r n ( x ) {\displaystyle {\begin{aligned}\mathrm {Kei} _{n}(x)&={\frac {1}{2}}\left({\frac {x}{2}}\right)^{-n}\sum _{k=0}^{n-1}\sin \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]{\frac {(n-k-1)!}{k!}}\left({\frac {x^{2}}{4}}\right)^{k}\\&+{\frac {1}{2}}\left({\frac {x}{2}}\right)^{n}\sum _{k\geq 0}\sin \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]{\frac {\psi (k+1)+\psi (n+k+1)}{k!(n+k)!}}\left({\frac {x^{2}}{4}}\right)^{k}\\&-\ln \left({\frac {x}{2}}\right)\mathrm {Bei} _{n}(x)-{\frac {\pi }{4}}\mathrm {Ber} _{n}(x)\end{aligned}}} Kei(x) pentru x {\displaystyle x} K e i ( x ) e x / 2 {\displaystyle \mathrm {Kei} (x)e^{x/{\sqrt {2}}}} x {\displaystyle x} unde ψ ( z ) {\displaystyle \psi (z)} funcția Digamma .
Cazul special Kei 0 ( x ) {\displaystyle _{0}(x)} ( x ) {\displaystyle (x)}
K e i ( x ) = − ln ( x 2 ) B e i ( x ) − π 4 B e r ( x ) + ∑ k ≥ 0 ( − 1 ) k ψ ( 2 k + 2 ) [ ( 2 k + 1 ) ! ] 2 ( x 2 4 ) 2 k + 1 {\displaystyle \mathrm {Kei} (x)=-\ln \left({\frac {x}{2}}\right)\mathrm {Bei} (x)-{\frac {\pi }{4}}\mathrm {Ber} (x)+\sum _{k\geq 0}(-1)^{k}{\frac {\psi (2k+2)}{[(2k+1)!]^{2}}}\left({\frac {x^{2}}{4}}\right)^{2k+1}} și dezvoltarea asimptotică:
K e i ( x ) ∼ − π 2 x e − x 2 [ f 2 ( x ) sin β + g 2 ( x ) cos β ] , {\displaystyle \mathrm {Kei} (x)\sim -{\sqrt {\frac {\pi }{2x}}}e^{-{\frac {x}{\sqrt {2}}}}[f_{2}(x)\sin \beta +g_{2}(x)\cos \beta ],} unde β {\displaystyle \beta } f 2 ( x ) {\displaystyle f_{2}(x)} g 2 ( x ) {\displaystyle g_{2}(x)} ( x ) {\displaystyle (x)}
Abramowitz and Stegun, Handbook of Mathematical Functions With Formulas, Graphs, and Mathematical Tables, Capitolul 9.9 .
Weisstein, Eric W. "Kelvin Functions." From MathWorld—A Wolfram Web Resource. [1] GPL-licensed C/C++ source code for calculating Kelvin functions at codecogs.com: [2] Arhivat în 7 aprilie 2007 , la Wayback Machine . 







 French
French Deutsch
Deutsch





![{\displaystyle \mathrm {Ber} _{n}(x)=\left({\frac {x}{2}}\right)^{n}\sum _{k\geq 0}{\frac {\cos \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]}{k!\Gamma (n+k+1)}}\left({\frac {x^{2}}{4}}\right)^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4a263b7ae69764facdf8d5e15fba1fc3c881552)



![{\displaystyle \mathrm {Ber} (x)=1+\sum _{k\geq 1}{\frac {(-1)^{k}(x/2)^{4k}}{[(2k)!]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a1665c8f8c8455c9690b5bd6a706fe45721959)
![{\displaystyle \mathrm {Ber} (x)\sim {\frac {e^{\frac {x}{\sqrt {2}}}}{\sqrt {2\pi x}}}[f_{1}(x)\cos \alpha +g_{1}(x)\sin \alpha ]-{\frac {\mathrm {Kei} (x)}{\pi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3799488c90b2998fbe42342cbada195c0bd9f2d0)






![{\displaystyle \mathrm {Bei} _{n}(x)=\left({\frac {x}{2}}\right)^{n}\sum _{k\geq 0}{\frac {\sin \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]}{k!\Gamma (n+k+1)}}\left({\frac {x^{2}}{4}}\right)^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a46b67988e6164f1ba8d04c28d321e50540b7b10)
![{\displaystyle \mathrm {Bei} (x)=\sum _{k\geq 0}{\frac {(-1)^{k}(x/2)^{4k+2}}{[(2k+1)!]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/897c4c42a2f29ca2704b4e0c306c7743d2281c5b)
![{\displaystyle \mathrm {Bei} (x)\sim {\frac {e^{\frac {x}{\sqrt {2}}}}{\sqrt {2\pi x}}}[f_{1}(x)\sin \alpha +g_{1}(x)\cos \alpha ]-{\frac {\mathrm {Ker} (x)}{\pi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ebcb459bc8a0a7c9f20c4cc42a5686bba13a091)



![{\displaystyle {\begin{aligned}\mathrm {Ker} _{n}(x)&={\frac {1}{2}}\left({\frac {x}{2}}\right)^{-n}\sum _{k=0}^{n-1}\cos \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]{\frac {(n-k-1)!}{k!}}\left({\frac {x^{2}}{4}}\right)^{k}\\&+{\frac {1}{2}}\left({\frac {x}{2}}\right)^{n}\sum _{k\geq 0}\cos \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]{\frac {\psi (k+1)+\psi (n+k+1)}{k!(n+k)!}}\left({\frac {x^{2}}{4}}\right)^{k}\\&-\ln \left({\frac {x}{2}}\right)\mathrm {Ber} _{n}(x)+{\frac {\pi }{4}}\mathrm {Bei} _{n}(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed3a1d5310d91ad74b82e32520bedda71d387a9b)


![{\displaystyle \mathrm {Ker} (x)=-\ln \left({\frac {x}{2}}\right)\mathrm {Ber} (x)+{\frac {\pi }{4}}\mathrm {Bei} (x)+\sum _{k\geq 0}(-1)^{k}{\frac {\psi (2k+1)}{[(2k)!]^{2}}}\left({\frac {x^{2}}{4}}\right)^{2k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fae7bb9569905c9119ac543e0878be564d56ca58)
![{\displaystyle \mathrm {Ker} (x)\sim {\sqrt {\frac {\pi }{2x}}}e^{-{\frac {x}{\sqrt {2}}}}[f_{2}(x)\cos \beta +g_{2}(x)\sin \beta ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/629b2c25ed4ccd9af090835f4e01f515b29dde4c)



![{\displaystyle {\begin{aligned}\mathrm {Kei} _{n}(x)&={\frac {1}{2}}\left({\frac {x}{2}}\right)^{-n}\sum _{k=0}^{n-1}\sin \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]{\frac {(n-k-1)!}{k!}}\left({\frac {x^{2}}{4}}\right)^{k}\\&+{\frac {1}{2}}\left({\frac {x}{2}}\right)^{n}\sum _{k\geq 0}\sin \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]{\frac {\psi (k+1)+\psi (n+k+1)}{k!(n+k)!}}\left({\frac {x^{2}}{4}}\right)^{k}\\&-\ln \left({\frac {x}{2}}\right)\mathrm {Bei} _{n}(x)-{\frac {\pi }{4}}\mathrm {Ber} _{n}(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7d4354383d7352bbe488b675c46c199a48d531)

![{\displaystyle \mathrm {Kei} (x)=-\ln \left({\frac {x}{2}}\right)\mathrm {Bei} (x)-{\frac {\pi }{4}}\mathrm {Ber} (x)+\sum _{k\geq 0}(-1)^{k}{\frac {\psi (2k+2)}{[(2k+1)!]^{2}}}\left({\frac {x^{2}}{4}}\right)^{2k+1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59abd87da4b10eab7d8b3e0fece097c16b09055a)
![{\displaystyle \mathrm {Kei} (x)\sim -{\sqrt {\frac {\pi }{2x}}}e^{-{\frac {x}{\sqrt {2}}}}[f_{2}(x)\sin \beta +g_{2}(x)\cos \beta ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40522fc03a68410e4e99609659c881142b74855b)


