Punct singular al unei curbe

În matematică un punct singular al unei curbe^[1] este un punct în care curba nu este dată de o funcție netedă^⁠(d) care poate conține un parametru. Definiția precisă a unui punct singular depinde de tipul de curbă studiată.

Curbele algebrice^⁠(d) plane pot fi definite drept mulțimea de puncte (x, y) care satisfac o ecuație de forma ${\displaystyle f(x,y)=0,}$ unde f este o funcție polinomială ${\displaystyle f:\mathbb {R} ^{2}\to \mathbb {R} .}$ Dacă f este explicitată ca

${\displaystyle f=a_{0}+b_{0}x+b_{1}y+c_{0}x^{2}+2c_{1}xy+c_{2}y^{2}+\cdots }$

și originea (0, 0) este pe curbă, atunci a₀ = 0. Dacă b₁ ≠ 0 atunci teorema funcției implicite^⁠(d) garantează că există o funcție netedă h astfel încât curba să aibă forma y = h(x) lângă origine. Similar, dacă b₀ ≠ 0 atunci există o funcție netedă k astfel încât curba să aibă forma x = k(y) lângă origine. În ambele cazuri, există o funcție netedă de la ${\displaystyle \mathbb {R} }$ la planul în care se află curba în vecinătatea originii. De reținut că în origine

${\displaystyle b_{0}={\frac {\partial f}{\partial x}},\;b_{1}={\frac {\partial f}{\partial y}},}$

deci curba este nesingulară^[1] sau regulată^[1] în origine dacă cel puțin una dintre derivatele parțiale ale lui f este diferită de zero. Punctele singulare sunt acele puncte de pe curbă în care ambele derivate parțiale se anulează:^[1]

${\displaystyle f(x,y)={\frac {\partial f}{\partial x}}={\frac {\partial f}{\partial y}}=0.}$

Se presupune că curba trece prin origine și ${\displaystyle y=mx.}$ Atunci f poate fi scrisă

${\displaystyle f=(b_{0}+mb_{1})x+(c_{0}+2mc_{1}+c_{2}m^{2})x^{2}+\cdots .}$

Dacă ${\displaystyle b_{0}+mb_{1}}$ nu este 0, atunci f = 0 are o soluție cu multiplicitatea 1 în x = 0 iar originea are un singur contact cu dreapta ${\displaystyle y=mx.}$ Dacă ${\displaystyle b_{0}+mb_{1}=0}$ atunci f = 0 are o soluție cu multiplicitatea 2 sau mai mare și dreapta ${\displaystyle y=mx,}$ sau ${\displaystyle b_{0}x+b_{1}y=0,}$ este tangentă la curbă. În acest caz, dacă ${\displaystyle c_{0}+2mc_{1}+c_{2}m^{2}}$ nu este 0 atunci curba are un punct de dublu contact cu ${\displaystyle y=mx.}$ Dacă coeficientul lui x², ${\displaystyle c_{0}+2mc_{1}+c_{2}m^{2},}$ este 0, dar coeficientul lui x³ nu este 0, atunci originea este un punct de inflexiune al curbei. Dacă coeficienții lui x² și x³ sunt ambii 0, atunci originea este un punct de ondulare al curbei. Această analiză poate fi aplicată oricărui punct al curbei prin translarea axelor de coordonate astfel încât originea să fie în punctul dat.^[2]

Dacă în dezvoltarea de mai sus b₀ și b₁ sunt ambele 0, dar cel puțin unul dintre c₀, c₁, c₂ nu este 0, atunci originea este un punct dublu al curbei. Punând din nou ${\displaystyle y=mx,}$ f poate fi scrisă

${\displaystyle f=(c_{0}+2mc_{1}+c_{2}m^{2})x^{2}+(d_{0}+3md_{1}+3m^{2}d_{2}+d_{3}m^{3})x^{3}+\cdots .}$

Punctele duble pot fi clasificate în funcție de soluțiile ecuației ${\displaystyle c_{0}+2mc_{1}+m^{2}c_{2}=0.}$

Dacă ${\displaystyle c_{0}+2mc_{1}+m^{2}c_{2}=0}$ are două soluții reale pentru m, adică dacă ${\displaystyle c_{0}c_{2}-c_{1}^{2}<0,}$ atunci originea este un nod.^[1] În acest caz curba se autointersectează în origine și are două tangente distincte corespunzătoare celor două soluții ale ${\displaystyle c_{0}+2mc_{1}+m^{2}c_{2}=0.}$ În acest caz funcția f are un punct șa în origine.

Un exemplu de nod este dat de ecuația ${\displaystyle x^{2}-y^{2}=0.}$

Dacă ${\displaystyle c_{0}+2mc_{1}+m^{2}c_{2}=0}$ nu are soluții reale pentru m, adică dacă ${\displaystyle c_{0}c_{2}-c_{1}^{2}>0,}$ atunci originea este un punct izolat. În planul real originea este un punct izolat (deși este „pe curbă”); totuși, atunci când este luată în considerare o curbă complexă, originea nu este izolată și are două tangente imaginare, corespunzătoare celor două soluții complexe ale ${\displaystyle c_{0}+2mc_{1}+m^{2}c_{2}=0.}$ Funcția f are în acest caz un extrem local în origine.

Un exemplu de punct izolat al unei curbe este dat de ecuația ${\displaystyle x^{2}+y^{2}=0.}$

Dacă ${\displaystyle c_{0}+2mc_{1}+m^{2}c_{2}=0}$ are o singură soluție cu multiplicitate 2 pentru m, adică dacă ${\displaystyle c_{0}c_{2}-c_{1}^{2}=0,}$ atunci originea este un punct de întoarcere. Curba în acest caz își schimbă direcția în origine creând un vârf ascuțit. Curba are o singură tangentă în origine care poate fi considerată drept două tangente care coincid.

Un exemplu de punct de întoarcere este dat de ecuația ${\displaystyle x^{3}-y^{2}=0.}$

Termenul nod poate fi folosit și pentru a indica un punct izolat, cu alte cuvinte un punct dublu care nu este un punct de întoarcere. Numărul de noduri și numărul de puncte de întoarcere de pe o curbă sunt doi dintre invarianții utilizați în formulele Plücker.

Dacă una dintre soluțiile ecuației ${\displaystyle c_{0}+2mc_{1}+m^{2}c_{2}=0}$ este și o soluție a ecuației ${\displaystyle d_{0}+3md_{1}+3m^{2}d_{2}+m^{3}d_{3}=0,}$ atunci ramura corespunzătoare a curbei are un punct de inflexiune în origine. În acest caz, originea este, după Hilton, un flecnod. Dacă ambele tangente au această proprietate, deci ${\displaystyle c_{0}+2mc_{1}+m^{2}c_{2}}$ este un factor al ${\displaystyle d_{0}+3md_{1}+3m^{2}d_{2}+m^{3}d_{3},}$ atunci originea este un biflecnod.^[3]

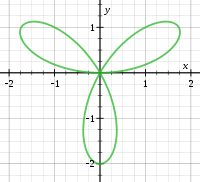
În general, dacă toți termenii de grad mai mici decât k sunt 0 și cel puțin un termen de grad k nu este 0 în f, atunci curba are un punct multiplu de ordinul k. Curba va avea, în general, k tangente în origine, deși unele dintre aceste tangente pot fi imaginare.^[4]

O curbă parametrică în ${\displaystyle \mathbb {R} ^{2}}$ este definită ca fiind o funcție ${\displaystyle g:\mathbb {R} \to \mathbb {R} ^{2},}$ ${\displaystyle g(t)=(g_{1}(t),g_{2}(t)).}$ Punctele singulare sunt acele puncte în care

${\displaystyle {\frac {dg_{1}}{dt}}={\frac {dg_{2}}{dt}}=0.}$

Multe curbe pot fi definite în orice mod, dar două definiții pot să nu fie identice. De exemplu, un punct de întoarcere poate fi definit pe o curbă algebrică, ${\displaystyle x^{3}-y^{2}=0,}$ sau pe o curbă parametrică, ${\displaystyle g(t)=(t^{2},t^{3}).}$ Ambele definiții produc un punct singular în origine. Totuși, un nod precum cel al ${\displaystyle y^{2}-x^{3}-x^{2}=0}$ în origine este o singularitate a curbei, considerată curbă algebrică, dar în varianta parametrică ${\displaystyle g(t)=(t^{2}-1,t(t^{2}-1)),}$ ${\displaystyle g'(t)}$ nu dispare niciodată. Prin urmare, nodul nu este o singularitate a curbei parametrice așa cum este definită mai sus.

Trebuie avut grijă atunci când se alege o parametrizare. De exemplu, dreapta y = 0 poate fi parametrizată prin ${\displaystyle g(t)=(t^{3},0)}$ care are o singularitate la origine. Atunci când este parametrizată cu ${\displaystyle g(t)=(t,0)}$, este nesingulară. Prin urmare, este mai corect din punct de vedere tehnic să se considere punctele singulare ale unei funcții netede decât un punct singular al unei curbe.

Definițiile de mai sus pot fi extinse pentru a acoperi curbele implicite care sunt definite drept mulțimea zero ${\displaystyle f^{-1}(0)}$ a unei funcții netede, și nu este necesar să fie o varietate algebrică^⁠(d). Definițiile pot fi extinse pentru a acoperi curbele din dimensiuni mai mari.

• en Hilton, Harold (1920). „Chapter II: Singular Points”. Plane Algebraic Curves. Oxford. 

Portal Matematică