Граф Дика — Википедия
| Граф Дика | |
|---|---|
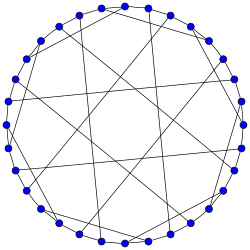 | |
| Вершин | 32 |
| Рёбер | 48 |
| Радиус | 5 |
| Диаметр | 5 |
| Обхват | 6 |
| Автоморфизмы | 192 |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Свойства | гамильтонов двудольный Граф Кэли |
Граф Дика — 3-регулярный граф с 32 вершинами и 48 рёбрами, назван в честь Вальтера фон Дика[1] [2].
Граф является гамильтоновым графом с 120 различными гамильтоновыми циклами. Его хроматическое число равно 2, хроматический индекс равен 3, его радиус равен 5, диаметр равен 5 и обхват равен 6. Он является также 3-вершинно-связным и 3-рёберно-связным.
Граф Дика является тороидальным, и двойственный граф его тороидального вложения — это граф Шрикханде, строго регулярный симметричный гамильтонов граф.
Алгебраические свойства
[править | править код]Группа автоморфизмов графа Дика — это группа порядка 192[3]. Она действует транзитивно на вершины и рёбра графа. Таким образом, граф Дика является симметричным. Он имеет автоморфизмы, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. В списке Фостера граф Дика, обозначенный как F32A, является единственным кубическим симметричным графом с 32 вершинами[4].
Характеристический многочлен графа Дика равен .
Карта Дика
[править | править код]Граф Дика является остовом[англ.] симметричного паркета поверхности третьего рода из двенадцати восьмиугольников, известного как карта Дика или Паркет Дика. Двойственный граф этого паркета является полным трёхдольным графом K4,4,4[5][6].
Галерея
[править | править код]- Альтернативное изображение графа Дика.
- Хроматическое число графа Дика равно 2.
- Хроматический индекс графа Дика равен 3.
Примечания
[править | править код]- ↑ W. Dyck. Über Aufstellung und Untersuchung von Gruppe und Irrationalität regulärer Riemann'scher Flächen // Math. Ann.. — Т. 17. — doi:10.1007/bf01446929.
- ↑ Weisstein, Eric W. Dyck Graph (англ.) на сайте Wolfram MathWorld.
- ↑ Royle, G. F032A data (недоступная ссылка)
- ↑ M. Conder, P. Dobcsányi. Trivalent symmetric graphs up to 768 vertices // J. Combin. Math. Combin. Comput.. — 2002. — Т. 40. — С. 41–63.
- ↑ W. Dyck. Notiz über eine reguläre Riemannsche Fläche vom Geschlecht 3 und die zugehörige Normalkurve 4. Ordnung // Math. Ann.. — 1880. — Т. 17. — С. 510–516.
- ↑ A. Ceulemans. The tetrakisoctahedral group of the Dyck graph and its molecular realization. // Molecular physics. — 2004. — Т. 102, вып. 11. — С. 1149-1163. — doi:10.1080/00268970410001728780.
Для улучшения этой статьи желательно:
|


 French
French Deutsch
Deutsch


