Фазовая диаграмма — Википедия

Фа́зовая диагра́мма (диаграмма состоя́ния) — графическое отображение равновесного состояния бесконечной физико-химической системы при условиях, отвечающих координатам рассматриваемой точки на диаграмме (носит название фигуративной точки).

Обычными координатами для построения фазовой диаграммы являются термодинамические параметры — температура и давление — и состав системы (в мольных или массовых процентах).

В общем случае количество координат превышает число компонентов системы на единицу (диаграмма однокомпонентной системы двумерна, двухкомпонентной — трёхмерна и т. п.) Для конденсированных систем зачастую не учитывают изменение фазовых равновесий за счёт давления, в этом случае число измерений диаграммы равно числу компонентов (диаграмма конденсированной двухкомпонентной системы двумерна, трёхкомпонентной — трёхмерна и т. п.) Сложные фазовые диаграммы в печатных изданиях изображают в виде сечений или проекций.

Согласно правилу фаз, на двумерной диаграмме однофазная область описывается полем, двухфазная — линией (на p–T диаграммах) или набором параллельных линий конод, для которых фиксированы составы равновесных фаз (на диаграммах с участием состава), трёхфазная — точкой (на p–T диаграммах) или горизонталью (на T–x или p–x диаграммах).

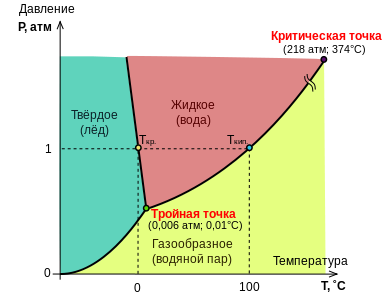
По правилу фаз, на фазовых диаграммах однокомпонентных систем поля соответствуют однофазным состояниям, линии, разграничивающие их — двухфазным, точки пересечения линий — трёхфазным (эти точки называют тройными точками).

Двухфазные линии, как правило, либо соединяют две тройные точки, либо тройную точку с точкой на оси ординат, отвечающую нулевому давлению. Исключение составляет линия жидкость–газ, заканчивающаяся в критической точке. При температурах выше критической различие между жидкостью и паром исчезает. На двухфазных линиях также находятся точки — температуры кристаллизации и кипения при нормальном давлении.

Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его.

Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его.

Рис. TG. Концентрационный треугольник Гиббса

Объёмная диаграмма состояния трёхкомпонентной системы представляет собой прямую трёхгранную призму, в основании которой лежит концентрационный треугольник Гиббса — Розебома, рёбра представляют собой оси температуры, а грани — диаграммы состояния трёх бинарных систем; геометрические элементы (точки и линии) внутри призмы отражают состояние трёхкомпонентной системы.

Для описания состава трёхкомпонентной системы обычно используют косоугольные координаты в виде треугольника Гиббса — Розебома^[1]. Применительно к фазовым диаграммам изображённый на рис. TG равносторонний концентрационный треугольник Гиббса (1875) представляет собой изотермическое сечение пространственной диаграммы в форме призмы (ось, перпендикулярная плоскости треугольника, — температура). Любая точка внутри треугольника Гиббса отвечает трёхкомпонентной системе; стороны треугольника отвечают двухкомпонентным системам, вершины — однокомпонентным (содержание компонента 100 %). Содержание каждого из компонентов тем больше, чем ближе расположена фигуративная точка системы к соответствующей вершине. При изображении состава системы по методу Гиббса длина каждого перпендикуляра, опущенного из фигуративной точки на сторону концентрационного треугольника, расположенную напротив вершины, соответствующей искомому компоненту — A, B или C, — отвечает содержанию в системе указанного в вершине компонента, а сумма длин перпендикуляров, опущенных из любой фигуративной точки внутри равностороннего треугольника на его стороны есть величина постоянная и равная высоте этого треугольника, принятой за 100 %^[1]. Для удобства треугольник размечают перпендикулярами, опущенными из вершин треугольника на противоположные им стороны, и линиями, параллельными сторонам треугольника. Для изображённой на рисунке фигуративной точки р доли компонентов A, B и C равны соответственно 50, 30 и 20 %.

При изображении состава системы по методу Розебома (1894), получившему большее распространение, нежели исходный метод Гиббса, используют шкалы, нанесённые на стороны равностороннего концентрационного треугольника Розебома (длина каждой стороны треугольника принята за100 %), и линии, параллельные сторонам треугольника^[2]. Любая из этих прямых есть геометрическое место точек с одинаковым содержанием компонента, характеризуемого вершиной треугольника против этой стороны, причём самой вершине соответствует 100 % компонента^[3]. Отсюда следует, что изначально существует два равноценных варианта выбора стороны концентрационного треугольника для нанесения шкалы искомого компонента, и выбор между этими сторонами произволен. Так, на рис. TR шкалу содержания компонента А можно разместить как на стороне АВ, так и на стороне АС. После того, как обсуждаемый выбор сделан, соответствие между двумя другими компонентами и используемыми для их шкал сторонами треугольника становится однозначным. Для изображённой на рис. TR фигуративной точки доли компонентов A, B и C равны соответственно 20, 20 и 60 %. Применительно к фазовым диаграммам треугольник Розебома представляет собой изотермическое сечение пространственной диаграммы в форме призмы (ось, перпендикулярная плоскости треугольника, — температура).

Рис. TD. Объёмная диаграмма состояния трёхкомпонентной системы с одной тройной эвтектикой при полном отсутствием растворимости компонентов в твёрдом состоянии и постоянном давлении

Изображённая на рис. TD пространственная диаграмма состояния трёхкомпонентной системы с одной тройной эвтектикой^[4] соответствует простейшему случаю, когда три компонента А, В и С в бинарных комбинациях А—В, В—С и С—А дают только простые эвтектики. Для изображения свойств такой системы строят прямую призму, в основании которой лежит треугольник Гиббса — Розебома; точки основания треугольника дают состав смесей, а на рёбрах призмы откладывают температуры. Точки А₁, B₁, С₁ отвечают температурам плавления чистых компонентов; кривые А₁r₁ и В₁r₁ есть кривые плавкости бинарных смесей А—В и лежат на грани А₁АВВ₁ призмы; r₁ — эвтектика бинарной системы А—В. Такими же эвтектиками являются s₁ в бинарной системе B—С и t₁ в бинарной системе С—A, лежащие на соответствующих гранях призмы; u₁ — тройная эвтектика, в которой в равновесии сосуществуют три твёрдые фазы и расплав, и в которой тройная смесь плавится/застывает как одно целое; r₁u₁, s₁u₁ и t₁u₁ — эвтектические кривые.

Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его.

Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его.

Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его.

Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его.

Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его.

Динамические:

• Дифференциальный термический анализ
• Визуальный термический анализ

Статические:

• Рентгенофазовый анализ
• Локальный рентгеноспектральный анализ

• Метод CALPHAD
• Метод выпуклых оболочек Г. Ф. Воронина

• Ларичева В. С., Ларичев Т. А. Химическая термодинамика. — Кемерово: КемГУ, 2015. — 240 с. — ISBN 978-5-8353-1755-4.
• Раковский А. В. Введение в физическую химию. — М.: Редакция химической литературы ГОНТИ НКТП, 1938. — 680 с.

• Фаза
• Правило фаз
• Правило рычага
• Инконгруэнтное плавление
• Конгруэнтное плавление
• Диаграмма состояния сплавов железо-углерод
• Тройная точка (фундаментальная точка)
• Основная тройная точка
• Дополнительные тройные точки
• Стабильная тройная точка
• Тройная эвтектическая точка
• Метастабильная тройная точка
• Четверная точка
• Критическая точка
• Особая точка
• Тройная линия
• Эвтектика
• Эвтектоид
• Перитектика
• Перитектоид
• Синтектика
• Монотектика