Квантовая хромодинамика — Википедия
Ква́нтовая хромодина́мика (КХД) — калибровочная теория квантовых полей, описывающая сильное взаимодействие элементарных частиц. Наряду с электрослабой теорией, КХД составляет общепринятый теоретический фундамент физики элементарных частиц.
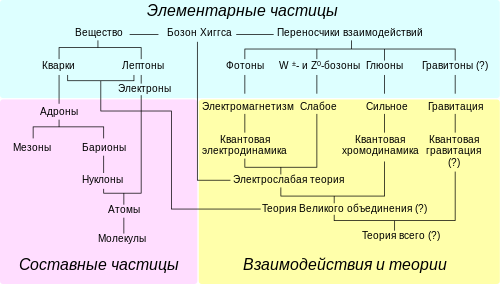
История КХД
[править | править код]С изобретением пузырьковой камеры и искровой камеры в 1950-х годах, экспериментальная физика элементарных частиц обнаружила большое и постоянно растущее число частиц, названных адронами. Стало ясно, что все они не могут быть элементарными. Частицы были классифицированы по электрическому заряду и изоспину; затем (в 1953 году)[1][2][3] Мюрреем Гелл-Манном и Кадзухико Нисидзимой — по странности. Для лучшего понимания общих закономерностей адроны были объединены в группы и по другим сходным свойствам: массам, времени жизни и прочим. В 1963 году Гелл-Манн и, независимо от него, Джордж Цвейг высказали предположение, что структура этих групп (фактически, SU(3)-мультиплетов) может быть объяснена существованием более элементарных структурных элементов внутри адронов. Эти частицы были названы кварками. Все адроны с барионным числом В = 0 (мезоны) состоят из пары «кварк и антикварк», а с числом В = 1 (барионы) — состоят из трёх кварков[4]. Всё многообразие известных на тот момент адронов могло быть построено всего из трёх кварков: u, d и s[5][6]. Впоследствии было открыто ещё три более массивных кварка. Каждый из этих кварков является носителем определённого квантового числа, названного его ароматом.
Однако в подобном описании одна частица, Δ++(1232), оказалась наделена необъяснимыми свойствами; в кварковой модели она составлена из трёх u-кварков со спинами, ориентированными в одном направлении, причём орбитальный момент их относительного движения равен нулю. Все три кварка в таком случае должны находиться в одном и том же квантовом состоянии, а так как кварк является фермионом, подобная комбинация запрещается принципом исключения Паули. В 1965 году Н. Н. Боголюбов, Б. В. Струминский и А. Н. Тавхелидзе[7], и также Хан Мо Ён[англ.] совместно с Йоитиро Намбу[8] и О. Гринбергом[англ.][9] независимо друг от друга решили эту проблему, предположив, что кварк обладает дополнительными степенями свободы калибровочной группы SU(3), позже названными «цветовыми зарядами». На необходимость приписать кваркам дополнительное число было указано Струминским в препринте от 7 января 1965 года[10][11]. Результаты работы Н. Н. Боголюбова, Б. Струминского и А. Н. Тавхелидзе были представлены в мае 1965 года на международной конференции по теоретической физике в Триесте[12]. Йоитиро Намбу представил свои результаты осенью 1965 года на конференции в США[13]. Хан и Намбу отметили, что кварк взаимодействует через октет векторных калибровочных бозонов, названных глюонами (англ. glue «клей»).
Поскольку свободных кварков не было обнаружено, считалось, что кварки были просто удобными математическими конструкциями, а не реальными частицами. Эксперименты по глубоко неупругому рассеянию электронов на протонах и связанных нейтронах показали, что в области больших энергий рассеяние происходит на каких-то элементах внутренней структуры, имеющих значительно меньшие размеры, чем размер нуклона: Ричард Фейнман назвал эти элементы «партонами» (так как они являются частями адронов). Результаты были окончательно проверены в экспериментах в SLAC в 1969 году. Дальнейшие исследования показали, что партоны следует отождествить с кварками, а также с глюонами.
Хотя результаты изучения сильного взаимодействия остаются немногочисленными, открытие асимптотической свободы Дэвидом Гроссом, Дэвидом Полицером и Франком Вильчеком позволило сделать множество точных предсказаний в физике высоких энергий, используя методы теории возмущений. Свидетельство существования глюонов было обнаружено в трёхструйных событиях в PETRA в 1979 году. Эти эксперименты становились всё более точными, достигая высшей точки в проверке пертурбативной КХД на уровне нескольких процентов в LEP в CERN.
Другая сторона асимптотической свободы — конфайнмент. Так как сила взаимодействия между цветовыми зарядами не уменьшается с расстоянием, предполагается, что кварки и глюоны никогда не могут быть освобождены из адрона. Этот аспект теории подтверждён расчётами решёточной КХД, но математически не доказан. Поиск этого доказательства — одна из семи «задач тысячелетия», объявленных Математическим институтом Клэя. Другие перспективы непертурбативной КХД — исследование фаз кварковой материи, включая кварк-глюнную плазму.
Формулировка КХД
[править | править код]Квантовое число «цвет»
[править | править код]Квантовая хромодинамика основывается на следующем постулате: каждый кварк обладает внутренним квантовым числом, условно называемым цветовым зарядом, или просто цветом. Термин «цвет», конечно же, не имеет никакого отношения к оптическим цветам и введён исключительно для целей популяризации. Инвариантная в цветовом пространстве комбинация является суммой трёх различных цветов: «красного» (), «зелёного» () и «синего» (), которые являются базисными векторами в этом пространстве. По аналогии с оптикой сумма «красного», «зелёного» и «синего» цветов даёт белый цвет (так называемое бесцветное состояние). Антикваркам соответствуют антицвета: «антикрасный» (), «антизелёный» () и «антисиний» (), причём комбинация «цвет + антицвет» также бесцветна. Глюонам соответствуют комбинации «цвет-антицвет», причём такие комбинации должны быть инвариантными относительно вращений в цветовом пространстве. Таких независимых комбинаций существует восемь:
- , , , , , , .
Первые шесть глюонов при этом являются цветными, а последние два – бесцветными. Цвет глюонов может быть также осмыслен как причина изменения цвета кварков при взаимодействии. Например, «синий» кварк может испустить «синий-антизелёный» глюон и превратиться при этом в «зелёный» кварк.
Лагранжиан КХД
[править | править код]Цвет — внутренняя степень свободы кварков и глюонов. Кварковому полю приписывается определённый вектор состояния единичной длины в комплексном трёхмерном цветовом пространстве C(3). Вращения в цветовом пространстве C(3), то есть линейные преобразования, сохраняющие длину, образуют группу SU(3), размерность которой равна 2·3²−3²−1=8.
Поскольку группа SU(3) связна, все её элементы можно получить экспоненцированием алгебры ASU(3). Следовательно, любое вращение в C(3)
можно представить в виде , где 3×3 матрицы (a = 1 … 8) называются матрицами Гелл-Манна и образуют алгебру ASU(3). Поскольку матрицы Гелл-Манна не коммутируют друг с другом, то есть , калибровочная теория, построенная на группе SU(3), является неабелевой (то есть является теорией Янга — Миллса).
Далее используется стандартный принцип калибровочной инвариантности. Рассмотрим лагранжиан свободного кваркового поля
Этот лагранжиан инвариантен относительно глобальных калибровочных преобразований кварковых и антикварковых полей:
где не зависят от координат в обычном пространстве.
Если же потребовать инвариантность относительно локальных калибровочных преобразований (то есть при ), то приходится вводить вспомогательное поле . В результате, лагранжиан КХД, инвариантный относительно локальных калибровочных преобразований, имеет вид (суммирование по ароматам кварков также предполагается)
где — тензор напряжённостей глюонного поля[англ.], а есть само глюонное поле.
Видно[источник не указан 393 дня], что этот лагранжиан порождает наряду с вершиной взаимодействия кварк-антикварк-глюон и трёхглюонные и четырёхглюонные вершины. Иными словами, неабелевость теории привела к взаимодействию глюонов и к нелинейным уравнениям Янга — Миллса.[источник не указан 393 дня]
Применимость КХД к реальным процессам
[править | править код]Расчёты на основе квантовой хромодинамики хорошо согласуются с экспериментом.
Высокие энергии
[править | править код]В разделе не хватает ссылок на источники (см. рекомендации по поиску). |
КХД уже достаточно давно с успехом применяется в ситуациях, когда кварки и глюоны являются адекватным выбором степеней свободы (при адронных столкновениях высоких энергий), в особенности, когда передача импульса от одной частицы к другой тоже велика по сравнению с типичным адронным энергетическим масштабом (порядка 1 ГэВ). Подробно про применение квантовой хромодинамики к описанию адронных столкновений см. в статье Современное состояние теории сильных взаимодействий.
Низкие энергии
[править | править код]При более низких энергиях, из-за сильных многочастичных корреляций работа в терминах кварков и глюонов становится малоосмысленной, и приходится на основе КХД строить эффективную теорию взаимодействия бесцветных объектов — адронов.
Однако начиная с 2008 года для КХД-расчётов стала активно и крайне плодотворно применяться методика КХД на решётке[англ.] — непертурбативный подход к квантовохромодинамическим расчётам, основанный на замене непрерывного пространства-времени дискретной решёткой и симуляции происходящих процессов с помощью метода Монте-Карло. Такие расчёты требуют использования мощных суперкомпьютеров, однако позволяют с достаточно высокой точностью рассчитывать параметры, вычисление которых аналитическими методами невозможно. Например, расчёт массы протона дал величину, отличающуюся от реальной менее чем на 2 %[14][15]. КХД на решётке также позволяет с приемлемой точностью рассчитывать и массы других, в том числе и ещё не открытых адронов, что облегчает их поиск.
В 2010 году с помощью решёточных расчётов была резко уточнена оценка массы u и d-кварков: погрешность снижена с 30 % до 1,5 %[16].
См. также
[править | править код]Примечания
[править | править код]- ↑ Nakano, T; Nishijima, N (1953). Charge Independence for V-particles. Progress of Theoretical Physics. 10 (5): 581. Bibcode:1953PThPh..10..581N. doi:10.1143/PTP.10.581.
- ↑ Nishijima, K (1955). Charge Independence Theory of V Particles. Progress of Theoretical Physics. 13 (3): 285–304. Bibcode:1955PThPh..13..285N. doi:10.1143/PTP.13.285.
- ↑ Gell-Mann, M (1956). The Interpretation of the New Particles as Displaced Charged Multiplets. Il Nuovo Cimento. 4 (S2): 848–866. Bibcode:1956NCim....4S.848G. doi:10.1007/BF02748000.
- ↑ С. С. Герштейн. Что такое цветовой заряд, или какие силы связывают кварки // Соровский образовательный журнал. — 2000. — № 6. — С. 78—84. Архивировано 14 января 2017 года.
- ↑ M. Gell-Mann (1964). A Schematic Model of Baryons and Mesons. Physics Letters. 8 (3): 214–215. Bibcode:1964PhL.....8..214G. doi:10.1016/S0031-9163(64)92001-3.
- ↑ Murray Gell-Mann: Selected Papers. — World Scientific, 2010.
- ↑ N. Bogolubov, B. Struminsky, A. Tavkhelidze. JINR Preprint D-1968, Dubna 1965.
- ↑ Han, M. Y.; Nambu, Y. (1965). Three-Triplet Model with Double SU(3) Symmetry. Phys. Rev. 139 (4B): B1006 – B1010. Bibcode:1965PhRv..139.1006H. doi:10.1103/PhysRev.139.B1006. Архивировано 18 февраля 2022. Дата обращения: 18 февраля 2022.
{{cite journal}}: Неизвестный параметр|deadlink=игнорируется (|url-status=предлагается) (справка) - ↑ Greenberg, O. W. (1964). Spin and Unitary Spin Independence in a Paraquark Model of Baryons and Mesons. Phys. Rev. Lett. 13 (20): 598–602. Bibcode:1964PhRvL..13..598G. doi:10.1103/PhysRevLett.13.598.
- ↑ Б. В. Струминский, Магнитные моменты барионов в модели кварков. ОИЯИ-Препринт P-1939, 1965.
- ↑ F. Tkachov, A contribution to the history of quarks: Boris Struminsky’s 1965 JINR publication Архивная копия от 6 октября 2016 на Wayback Machine
- ↑ A. Tavkhelidze. Proc. Seminar on High Energy Physics and Elementary Particles, Trieste, 1965, Vienna IAEA, 1965, p. 763.
- ↑ К вопросу об открытии квантового числа «ЦВЕТ» Архивная копия от 4 марта 2016 на Wayback Machine на сайте ИЯИ РАН.
- ↑ S. Dürr, Z. Fodor, J. Frison, C. Hoelbling, R. Hoffmann, S. D. Katz, S. Krieg, T. Kurth, L. Lellouch, T. Lippert, K. K. Szabo, and G. Vulvert. Ab Initio Determination of Light Hadron Masses (англ.) // Science. — 2008. — 21 November (vol. 322, no. 5905). — P. 1224—1227. — doi:10.1126/science.1163233. — . — PMID 19023076.
- ↑ Учёные подтвердили знаменитую формулу Эйнштейна. Membrana (24 ноября 2008). Дата обращения: 1 марта 2012. Архивировано из оригинала 27 мая 2012 года.
- ↑ Легчайшие кварки взвешены с невероятной точностью. Membrana (7 апреля 2010). Дата обращения: 1 марта 2012. Архивировано из оригинала 27 мая 2012 года.
Литература
[править | править код]- Jean Letessier, Johann Rafelski, T. Ericson, P. Y. Landshoff. Hadrons and Quark-Gluon Plasma. — Cambridge University Press, 2002. — 415 p. — ISBN 9780511037276.
Учебная
[править | править код]- Альтарелли Г. Введение в КХД Архивная копия от 16 ноября 2013 на Wayback Machine (лекции, прочитанные на Европейской школе по физике высоких энергий)
- Индурайн Ф. Квантовая хромодинамика. — М.: Мир, 1986. — 288 с.
Историческая
[править | править код]- С. Адлер Заметки к истории квантовой хромодинамики Архивная копия от 5 декабря 2015 на Wayback Machine (англ.)
- V. A. Matveev, A. N. Tavkhelidze. The quantum number color, colored quarks and QCD (Dedicated to the 40th Anniversary of the Discovery of Color) Архивная копия от 5 марта 2022 на Wayback Machine
- А. Н. Тавхелидзе. К вопросу об открытии квантового числа «ЦВЕТ» Архивная копия от 4 марта 2016 на Wayback Machine
- F. Tkachov, A contribution to the history of quarks: Boris Struminsky’s 1965 JINR publication Архивная копия от 6 октября 2016 на Wayback Machine (англ.)
- Видео Лекции: Теория сильных взаимодействий (профессор Фадин В. С., 2014 г.) Архивная копия от 18 февраля 2015 на Wayback Machine
Ссылки
[править | править код]- И. М. Дрёмин, А. Б. Кайдалов Квантовая хромодинамика и феноменология сильных взаимодействий Архивная копия от 17 января 2008 на Wayback Machine // Успехи физических наук, том 176, № 3., с. 275, 2006 г
- КХД в Информационной теории всего Архивная копия от 3 февраля 2020 на Wayback Machine


 French
French Deutsch
Deutsch
















![{\displaystyle [t^{a},t^{b}]=i\,f_{c}^{ab}t^{c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e592f16db7febc2e119a3d3317b1e06ca8955262)






![{\displaystyle G_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }-ig[A_{\mu },A_{\nu }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a4251cbc7e5f409e37cb8ec5163f0c33f544248)
