Неустойчивость Рэлея — Тейлора — Википедия
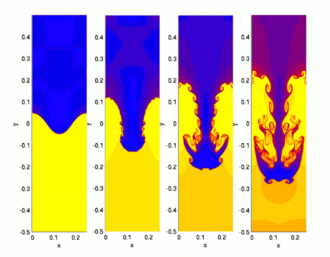
Неустойчивость Рэлея — Тейлора (названа в честь лорда Рэлея и Дж. И. Тейлора) — самопроизвольное нарастание возмущений давления, плотности и скорости в газообразных и жидких средах с неоднородной плотностью, находящихся в гравитационном поле (Рэлей, 1900 г.) либо движущихся с ускорением (Тейлор, 1950 г.).
Частными случаями неустойчивости Рэлея — Тейлора являются неустойчивости границ сред с разной плотностью при ускорении под воздействием от проходящей ударной волны (неустойчивость Рихтмайера — Мешкова) и неустойчивость плазмы, находящейся в поле тяготения над параллельным по отношению к её границе магнитным полем (неустойчивость Крускала — Шварцшильда)
Простейший случай неустойчивости Рэлея — Тейлора — неустойчивость поверхности раздела жидкостей либо газов с различными плотностями в поле тяготения, когда слой более плотной среды лежит в неустойчивом равновесии на слое менее плотной. Если в начальном состоянии плоскость раздела перпендикулярна вектору силы тяжести, то любое возмущение поверхности раздела будет расти с течением времени, так как участки более плотной среды, оказавшиеся выше плоскости раздела, начинают «тонуть» в менее плотной среде, а участки менее плотной среды, оказавшиеся ниже плоскости раздела, начинают «всплывать» в более плотной среде. Такое взаимное проникновение ведет к уменьшению потенциальной энергии системы, которая достигает минимума, когда слои полностью меняются местами, то есть система достигает устойчивого равновесия.
Основным параметром, определяющим скорость развития этой неустойчивости, является число Атвуда.
Аналитическое описание
[править | править код]Задача о неустойчивости Рэлея — Тейлора имеет аналитическое решение в рамках линейной теории устойчивости.
Пусть два протяжённых плоских горизонтальных слоя жидкости расположены в поле тяжести друг над другом, причём более тяжёлая жидкость 1 находится вверху (на иллюстрации — синий цвет), плотности жидкостей . Верхняя и нижняя границы — твёрдые. Для простоты удобно пользоваться моделью невязкой несжимаемой жидкости, тогда система описывается уравнением Эйлера:
В дальнейшем компоненты скорости определяются как . Вполне очевидно, что равновесное решение () удовлетворяет модели, при этом из уравнения Эйлера для давления получается следующее:
Откуда определяется равновесное распределение давления (известный результат для давления столба жидкости):
Внесём в равновесное состояние малые возмущения. Пусть скорость настолько мала, что можно пренебречь нелинейным слагаемым в уравнении Эйлера, а давление имеет вид , где . Тогда получим линейную систему уравнений для малых возмущений (далее штрих у давления опущен):
Граничные условия задаются исходя из соображений равенства z-компонент скорости жидкостей 1 и 2 на границе раздела и наличия поверхностного натяжения. На верхней и нижней границах, так как жидкость идеальная, работают условия непротекания. Удобно принять координату границы раздела в равновесии за 0. На ней выполняется кинематическое условие
и динамическое условие
Условие непротекания верхней и нижней границ:
где — величина отклонения границы от невозмущённой, — коэффициент поверхностного натяжения. Полученная задача для возмущений легко решается.
Положим, что возмущения имеют вид:
где — скорость роста (инкремент) возмущения, — компоненты волнового вектора возмущения границы.
Из уравнения Эйлера выражается :
а условие несжимаемости даёт уравнение Лапласа для давления. В итоге, скорость течения из задачи удаётся исключить. Остаётся линейное уравнение:
с граничными условиями:
Решение уравнения Лапласа для давления:
Константы определяются из кинематического условия. Динамическое условие даёт связь между инкрементом и модулем волнового вектора
откуда непосредственно следует выражение для критического волнового числа возмущений (при ):
- .
Если длина волны больше критической, то возмущения границы будут нарастать.
В предельном случае бесконечно глубоких слоёв () наибольшая скорость роста возмущений достигается при волновом числе
- .
В тонких слоях ():
- .
В природе
[править | править код]- Ярким известным проявлением неустойчивости Рэлея — Тейлора являются вымеобразные облака, а также ядерный гриб и экваториальные ионосферные пузыри.
См. также
[править | править код]Литература
[править | править код]- Лабунцов Д. А., Ягов В. В. Механика двухфазных систем. // М.: Изд-во МЭИ, 2000. — с. 143—146.
- Векштейн Г. Е. Физика сплошных сред в задачах. // М.: Институт компьютерных исследований, 2002. — с. 109—111.
Ссылки
[править | править код]- http://www.astronet.ru/db/msg/1188634 Архивная копия от 25 ноября 2010 на Wayback Machine


 French
French Deutsch
Deutsch




































