Расчётная сетка — Википедия

Расчётная (вычислительная) сетка — совокупность точек (сеточных узлов), заданных в области определения некоторой функции .

Расчётные сетки используются при численном решении дифференциальных и интегральных уравнений. Качество построения расчётной сетки в значительной степени определяет успех (неудачу) численного решения уравнения.
Классификация и методы построения расчётных сеток
[править | править код]Процедуру построения расчётной сетки можно рассматривать как построение взаимно-однозначного отображения области определения функции (физической области) на некоторую расчётную область, имеющую более простую форму.
Алгебраические методы построения сетки
[править | править код]Алгебраические сетки строятся путём решения алгебраических уравнений. Примером простейшей сетки, заданной на отрезке, может служить множество {xk}={x1, x2 … xK}, где xk=x1+dx*(k-1). Величина dx в этом случае называется шагом расчётной сетки. Основными достоинствами алгебраических методов являются хороший контроль распределения внутренних узлов сетки и высокая эффективность их численной реализации, что особенно важно при построении адаптивных (перестраивающихся в процессе расчёта) сеток. Недостаток алгебраических методов заключается в распространении разрывов границ внутрь области. Применение дифференциальных методов, как правило, позволяет получать более гладкие сетки.
Дифференциальные методы построения сетки
[править | править код]Построение сеток методом конформных отображений
[править | править код]Недостаток методов построения расчётных сеток, использующих метод конформных отображений, заключается в том, что они пригодны лишь для построения двумерных сеток.
Сетки, связанные (согласованные) с границей области
[править | править код]Простейший способ построения расчётной сетки заключается в разбиении пространства системой поверхностей, эквидистантных базовым поверхностям стандартных координатных систем, что позволяет существенно упростить запись решаемых дифференциальных уравнений. Недостаток интерференционной концепции заключается в несвязанности сетки с формой границ области — при рассмотрении областей определения функции произвольной формы, ни одна из координатных линий не совпадает с границей, что приводит к снижению качества реализации граничных условий и (или) к чрезвычайному усложнению расчётного алгоритма и, как следствие, к увеличению затрат машинного времени. За счёт использования криволинейных сеточных линий, можно добиться совпадения границ области определения функции (физической области) и сеточных линий, что позволяет упростить запись граничных условий. Однако, вследствие преобразования координат, в уравнении, подлежащем решению, как правило, появляются дополнительные члены.
Структурированные (регулярные) сетки
[править | править код]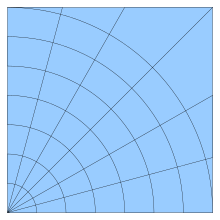
В тех случаях, когда множество сеточных узлов является упорядоченным расчётная сетка называется структурированной. Использование структурированных сеток (по сравнению с неструктурированными) позволяет, как правило, уменьшить продолжительность расчёта и необходимый объём оперативной памяти ЭВМ. В то же время процедура построения криволинейной регулярной сетки, как правило, требует больших затрат труда и ресурсов ЭВМ, по сравнению с процедурой построения нерегулярной сетки.

Ортогональные и ортогонализованные сетки
[править | править код]Для получения решения дифференциального уравнения, имеющего требуемую точность при минимальных затратах ресурсов ЭВМ, расчётная сетка должна обладать рядом свойств. В частности, как показывает опыт многих исследователей, расчётные ячейки должны обладать малой скошенностью, то есть расчётная сетка должна быть, по возможности, ортогонализованной. Задача построения многомерной ортогонализованной расчётной сетки формулируется как задача о минимизации функционала I=int(wQ dV), где w — весовая функция, Q — мера ортогональности сетки. В качестве меры Q может быть использована сумма скалярных произведений касательных к координатным линиям сетки. Можно показать, что вариационная задача о построении ортогонализованной расчётной сетки сводится к краевой задаче для системы дифференциальных уравнений Пуассона. Как известно, система уравнений Пуассона при заданных граничных условиях описывает распределение тепла в рассматриваемом объёме, что позволяет рассчитывать на получение гладких сеточных линий, даже в тех случаях когда границы физической области имеют изломы. Принцип максимума, справедливый для эллиптических уравнений, гарантирует, что максимальные и минимальные значения расчётных координат будут достигаться на границах области. Поскольку используется система эллиптических уравнений, в качестве граничных условий должны задаваться либо координаты узлов сетки на границах (условие Дирихле) либо наклон координатных линий на границах (условие Неймана).
В задачах с разрывными решениями (в том числе в задачах сверхзвуковой газодинамики) расчётная область характеризуется наличием разномасштабных элементов сложной неоднородной структуры. Достаточно большие зоны имеют малые или умеренные градиенты параметров решения. Вместе с тем встречаются сравнительно узкие области, градиенты параметров решения в которых достигают больших величин. Это — ударные волны, контактные разрывы, пограничные слои. Для получения достоверного численного решения задач такого типа необходимо использовать расчётные сетки с малыми пространственными шагами. Вычислительные затраты при этом становятся столь значительными, что из-за ограничений вычислительной техники не всегда удаётся получить достаточно точное решение задач. В подобных случаях становится желательным применение динамически адаптивных сеток, позволяющих использование малых пространственных шагов сетки, где это необходимо, для соблюдения жёстких требований к численным методам, но при этом сохраняя умеренные требования к вычислительной технике. Методы динамически адаптивных сеток являются одним из наиболее эффективных подходов для повышения точности численного решения в расчётных областях с несколькими пространственными масштабами, отражающими неоднородную структуру решения. Основная идея методов динамически адаптивных сеток состоит в уменьшении размеров ячеек в тех зонах расчётной области, в которых возникают большие ошибки решения. Так как в большинстве случаев искомое решение неизвестно и невозможно определить ошибку, представляющую собой разность точного и приближённого решения в некоторой норме, то в качестве меры ошибки решения чаще всего используют градиенты или разности параметров решения. Выделяют два этапа процесса адаптации: работу критерия и собственно адаптационные процедуры.
Процедуры адаптации. В литературе отмечаются следующие основные подходы: полная регенерация сетки; локальное дробление-слияние ячеек; перемещение узлов. Полная регенерация сетки заключается в построении новой сетки с использованием информации, полученной на старой сетке, и переинтерполяцией решения. В методе перемещения узлов предполагается, что общее число расчётной сетки фиксировано. Их перераспределение также осуществляется с целью повышения густоты сетки в областях локализации особенностей решения и разрежения её там, где такие особенности отсутствуют. Метод локального дробления-слияния ячеек расчётной сетки сводится к включению в сетку дополнительных узлов в окрестностях локализации особенностей решения с одновременным удалением лишних узлов в регионах, где решение не содержит особенностей. При двух крайних методах необходимо поддерживать необходимое качество расчётной сетки.
Многоблочные сетки
[править | править код]
Литература
[править | править код]- Андерсон Д., Таннехил Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен: В 2-х т.: Пер. с англ. — М.: Мир, 1990.
- Флетчер К. Вычислительные методы в динамике жидкостей. М. Мир, 1991, в 2-х т.
- Thompson Joe F., Warsi Z. A., Mastin C. V. Numerical Grid Generation, Foundations and Applications. — Amsterdam: North-Holland, 1985
См. также
[править | править код]- Конечные разности
- Разностная схема
- МКЭ
- Метод конечных разностей
- Триангуляция Делоне
- Полигональная сетка
- en:Regular grid
- Адаптивная сетка[англ.]
- en:Unstructured grid
Для улучшения этой статьи по математике желательно: |


 French
French Deutsch
Deutsch
