Algoritm – Wikipedia

Den här artikeln behöver fler eller bättre källhänvisningar för att kunna verifieras. Motivering: Finns bara källor om inledande texten och om en detaljuppgift (2016-09) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

En algoritm är, inom matematiken och datavetenskapen, en ändlig uppsättning (mängd) otvetydiga instruktioner som efter exekvering löser ett problem.^[1] Algoritmen startar i ett givet tillstånd (starttillstånd) och når resultatet (sluttillstånd) inom ett ändligt antal steg. Varje steg måste vara tydligt och precist definierat, på så sätt att utomstående ska kunna exekvera algoritmen och verifiera ett resultat. Ytterligare är effektivitet viktigt, det vill säga varje steg måste vara elementärt och exakt, samt gå att beräkna inom en ändlig tidsram. Det yttersta kriteriet för effektiva algoritmer är dess beräkningskomplexitet, något som mäts i antalet beräkningssteg som krävs för att nå ett resultat. Vanligtvis är det tidskomplexitet som mäts för att särskilja algoritmer, som uppmäts i tidsmängd beroende på problemstorleken.^[2] Det går även att mäta minneskomplexitet där man mäter hur mycket minne som krävs för att lösa ett problem.^[3] Utifrån ett problems algoritm kan man klassificera problem efter svårighetsgrad i så kallade komplexitetsklasser. Med klasser för tidskomplexitet är det möjligt att avgöra vilka problem som går att lösa inom en rimlig tid.^[4]

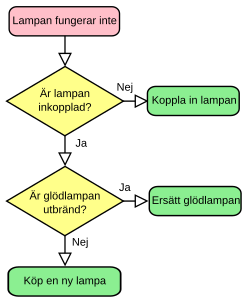
Informellt illustreras algoritmer ofta som ett recept (även om många algoritmer är mycket mer komplexa än recept). Konceptuellt blir då ingredienser indata, receptet själva algoritmen och maträtten ett resultat. Men istället för att blanda eller koka finns det andra grundläggande steg i algoritmer. Man brukar räkna de fyra räknesätten och de logiska operationer på sanningsvärden som grundläggande operationer, man säger att de är atomära. Dessutom krävs att man till minne kan både läsa och skriva data. Det är ett mycket känt bevis av Alan Turing för vilka operationer som krävs för att kunna beräkna vilken funktion som helst.^[2]

Ursprunget för begreppet algoritm uppstod som ett sätt att beskriva procedurer för att lösa matematiska problem som exempelvis att finna den gemensamma delaren för två tal eller att multiplicera två tal. Begreppet formaliserades 1936 genom Alan Turings turingmaskin och Alonzo Churchs lambdakalkyler, som i sin tur lade grunden för datavetenskapen.^{[källa behövs]}

De flesta algoritmer implementeras som datorprogram, då man strukturerar dem i programform. För att uttrycka program används programspråk som är formella språk med samtliga nödvändiga operationer för att uttrycka en godtycklig beräkningsbar funktion.

Ordet algoritm bör ej förväxlas med den matematiska termen logaritm.

För många problem finns flera algoritmer att välja mellan. De använder olika instruktioner och kan kräva olika mycket resurser som antal steg, eller operationer, och storlek på minne, för att lösa samma problem. Ett annat ord för algoritmens resursberoende är komplexitet. För att på ett meningsfullt sätt kunna jämföra algoritmer är det viktigt att man specificerar en beräkningsmodell som är rimlig för det problem som ska lösas. Om man vill implementera en snabb multiplikation av stora tal kanske man väljer att räkna antalet elementära additioner och multiplikationer, medan den som väljer mellan sorteringsalgoritmer antagligen föredrar att räkna antalet jämförelser som utförs. För de allra flesta tillämpningar använder man sig idag av modellen Random Access Machine där man ger alla minnesreferenser samma kostnad (enhetskostnad) och alla elementära operationer också anses ha samma kostnad.

Hur många steg eller hur mycket minne en algoritm behöver är olika för olika indata. Även med en enkel beräkningsmodell är det ofta ett oöverstigligt problem att uppskatta hur många operationer eller hur mycket minne en algoritm behöver, räknat som funktion av indatas storlek. Därför väljer man oftast att diskutera en algoritms asymptotiska tids- eller minneskomplexitet, det vill säga hur antalet steg växer som funktion av indatastorleken.

Det man antagligen mest är intresserad av är en algoritms förväntade komplexitet. Tyvärr är detta ofta mycket svårt att studera, och kräver dessutom många antaganden om de indata man har. (Vilken sannolikhetsfördelning har talen som ska multipliceras?) Mer praktiskt, och ofta mycket avslöjande, är att göra en värsta-fallet-analys där man tittar på hur komplexiteten blir när man har som mest ogynnsamma omständigheter.

Effektiviteten bedöms i tre olika avseenden:

1 - Den algoritm är effektivast som löser problemet på kortast tid.

För att mäta tiden kan det därför vara nödvändigt att testköra varje algoritm på en hel uppsättning olika problem och därefter poängsätta varje algoritm efter hur den skötte sig jämfört med de övriga.

2 - Den algoritm är effektivast, som löser problemet med minst resurser.

I datorsammanhang handlar det oftast om hur mycket minne algoritmen tar i anspråk för att lösa ett problem.

3 - Den algoritm är effektivast, som är minst komplicerad.

Detta är oftast (men inte alltid) liktydigt med mängden kod, som går åt till att beskriva algoritmen.

Genom att testköra olika algoritmer på lämpligt sätt kan man relativt lätt avgöra vilken av en given grupp algoritmer som är effektivast med avseende på det första och andra kriteriet. Genom att analysera koden för varje algoritm kan man också avgöra vilken som är effektivast med avseende på det andra och tredje kriteriet. Bäst är naturligtvis om man kan visa att en viss algoritm är den effektivaste i samtliga tre avseenden. Det är däremot mycket svårt att avgöra om den algoritm man tagit fram är den absolut effektivaste av alla möjliga algoritmer. Även för mycket enkla algoritmer är sådana bevis så svåra att genomföra att man i regel måste nöja sig med 'det bästa hittills'.

En av de enklaste algoritmerna går ut på att finna det största talet i en (osorterad) lista med tal. Lösningen kräver att man tittar på varje tal i listan, men endast en gång. Beskriven i ord lyder algoritmen som följer:

1. Anta att det första talet är störst och notera det talet.
2. Ta ställning till varje återstående tal i listan och om något är större än det dittills största talet, notera det i stället för det tidigare noterade talet.
3. När hela listan gåtts igenom är det senast noterade talet det största.

Här följer en mer formell beskrivning av algoritmen i pseudokod:

  Algoritm StörstaTal   Invärden: En icke-tom lista, L, som innehåller tal.   Resultat: Det största talet i listan, L.    största ← L0   för varje tal i listan L≥1, upprepa     om tal > största, så       största ← tal   returnera största 

Algoritmer är inte begränsade till datalogi eller beräkningar utan kan även användas till annan problemlösning. Ett recept för en maträtt kan till exempel innehålla en beskrivning, en algoritm, av hur man lagar rätten.

För ett mer komplext exempel, se Euklides algoritm, vilken är en av de äldsta kända matematiska algoritmerna.

Ordet algoritm kommer från arabiska och ursprungligen från namnet på den persiska (iranska) matematikern Mohammad ibn Musa, kallad al-Khwarazmi, "mannen från Kharazm" (idag Chiva i Uzbekistan)^[5], som levde i Baghdad ca 780-850 e.Kr. Genom tiderna har ordet förändrats och kombinerats med grekiskans arithmo's som betyder siffra och beräkning.

• Binärsökning
• Bredd-först-sökning
• Djup-först-sökning
• Djikstras algoritm
• Euklides algoritm
• Kruskals algoritm
• Databrytningsalgoritm
• Genetiska algoritmer
• Maskininlärningsalgoritmer
• Slumptalsgenerator
• Sorteringsalgoritmer

• Algoritmisk handel
• Algoritmisk talteori
• Artificiell intelligens
• Girig algoritm
• Muhammad ibn Musa al-Khwarizmi
• Pseudokod

• Janlert, Lars-Erik, 1950- (2000 ;). Datatyper och algoritmer. Studentlitteratur. ISBN 9144013647. OCLC 186568746. http://worldcat.org/oclc/186568746. Läst 4 juni 2019 
• Introduction to Algoritms : Thomas H. Cormen