Diracs delta-funktion – Wikipedia

Diracs delta-funktion (även kallad Dirac-pulsen eller enhetsimpuls eller diracdistributionen) efter Paul Dirac, betecknas ${\displaystyle \delta (t)}$ och är en distribution, definierad av hur den beter sig när den är en del av en integrand:

${\displaystyle \int _{a}^{b}f(t)\,\delta (t-t_{0})~dt={\begin{cases}f(t_{0})&{\mbox{om }}a<t_{0}<b\\0&{\mbox{annars}}\end{cases}}}$

Distributionen kan ses som gränsvärdet då basen i en rektangel med arean 1 och ett hörn i origo går mot noll. Detta gör att den även kan ses som en funktion vars värde är lika med noll överallt utom i punkten ${\displaystyle t=0}$.

Den tidsdiskreta versionen av delta-funktionen ${\displaystyle \delta (n)}$ är noll överallt utom för ${\displaystyle n=0}$ då den är lika med 1.

Diracs delta-funktion kan ses som derivatan av Heavisidefunktionen^[1].

Bör inte förväxlas med Kroneckerdelta.

Ponera att man har en stav med en inhomogen yta där tjockleken på staven varierar och en funktion f som beskriver masstätheten längs med staven. Fysikaliskt definierar den massan per längdenhet på staven i punkten t och matematiskt definieras den som en funktion så att massan i ett intervall a till b är

${\displaystyle \int _{a}^{b}f(t)dt}$

Däremot om massan fördelas över staven i ett begränsat antal punkter och inte kontinuerligt så fallerar ovanstående beskrivning. Om man tänker sig att vi har en tråd med försumbar massa med en liten men tung droppe fasthängd i mitten vid ${\displaystyle t=0}$, och antar att droppen har en massa och är så liten att den matematiskt kan beskrivas som en punkt. Massan (integralen av funktionen) är noll på intervallet ${\displaystyle [a,b]}$ om 0 ligger utanför intervallet och ett om 0 ingår i intervallet. Det finns dock ingen funktion som har dessa egenskaper. Om det fanns så skulle man ha ${\displaystyle f(t)=0}$ för alla ${\displaystyle t\neq 0}$, eftersom massan per längdenhet är noll utom i ${\displaystyle t=0}$. Det som händer då en funktion är noll utom i en punkt är att man kan visa att integralen måste vara noll. Då man integrerar över ett intervall där ${\displaystyle t=0}$ ingår så kommer man aldrig att kunna erhålla det korrekta värdet ett. Ur en fysikalisk synvinkel är masstätheten 0 utom i ${\displaystyle t=0}$ där den är oändlig emedan en begränsad massa är koncentrerad i ett intervall där längden är noll. Därmed erhåller vi en integral som är icke-noll. Dirac införde en funktion ${\displaystyle \delta (t)\,\!}$ med dessa egenskaper som definieras enligt följande:

${\displaystyle \delta (t)=0\,\!}$ för ${\displaystyle t\neq 0}$

och

${\displaystyle \int _{a}^{b}f(t)dt=1~~a<0<b}$

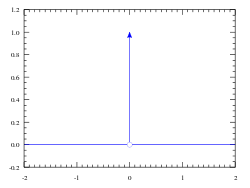
Vi säger att dessa två räknelagar gäller för Diracs deltafunktion.

${\displaystyle \delta (x)={\begin{cases}\infty ,&x=0\\0,&x\neq 0\end{cases}}}$

${\displaystyle \int _{-\infty }^{\infty }\delta (x)\,dx=1.}$

Det finns dock ingen vanlig funktion som har dessa egenskaper. Vanligtvis definieras Diracfunktionen som ett mått eller som en distribution. Ur ovanstående räknelagar kan vi erhålla dessa viktiga egenskaper;

${\displaystyle \int _{-\infty }^{\infty }f(t)\,\delta (t-t_{0})~dt=f(t_{0})}$

och

${\displaystyle f(t)\delta (t-t_{0})=f(t_{0})\delta (t-t_{0})\,\!}$

för varje funktion ${\displaystyle f(t)\,\!}$ som är kontinuerlig i ${\displaystyle t_{0}\,\!}$

Man kan tänka sig att man skapar deltafunktionen genom att låta den vara en "lådfunktion" som har den konstanta arean 1. Det man sedan gör är att man låter basen, som är parallell med x-axeln, närma sig origo samtidigt som man låter höjden, som är parallell med y-axeln, öka. Antag att vi har en funktion, ${\displaystyle f_{1}(x)\,\!}$ där höjden är 1 och bredden 1. Skapa sen en funktion, ${\displaystyle f_{2}(x)\,\!}$ där höjden är 2 och bredden 1/2. Fortsätt genom att skapa en funktion, ${\displaystyle f_{3}(x)\,\!}$ med höjden 4 och bredden 1/4. Sista steget är att skapa en funktion, ${\displaystyle f_{4}(x)\,\!}$ där höjden är 8 och bredden en 1/8. Det som nu sker är att höjden på kurvan stadigt stiger medan bredden på kurvan minskar. Detta kommer slutligen att rendera ett rakt streck, ju smalare man gör bredden. Dessutom, det alla dessa funktioner har gemensamt är att deras integraler, bredden x höjden = 1. Detta är hur man intuitivt "bevisar" Diracs deltafunktion. Det är ju egentligen ingen riktigt funktion utan är som enligt ovan nämnt en distribution.

Ett sätt att rigoröst definiera Diracs deltafunktion är att definiera den som ett mått ${\displaystyle \delta }$. För en delmängd A till de reella talen definierar man Diracmåttet med:

${\displaystyle \delta (A)={\begin{cases}0&x\notin A\\1&x\in A\end{cases}}}$

Med hjälp av Lebesgueintegration kan man sedan definiera integration med avseende på Diracmåttet. Man får då att:

${\displaystyle \int _{\mathbb {R} }fd\delta =f(0)}$

• Deltaföljden

• Claes Jogréus och Håkan Lennerstad, Serier och Transformer, Studentliteratur.
• D.H. Griffel, Applied Functional Analysis, John Wiley & Sons, 1984.

• Delta Function på MathWorld
• Dirac Delta Function på PlanetMath