Disjunktion – Wikipedia
| Logisk operator (Logisk grind) |
|---|
|
| Se även |
Disjunktion, som i satslogiken är liktydigt med inklusiv disjunktion, är en logisk operator. Generellt skiljer man inom logik och språk på inklusiv disjunktion eller svag disjunktion, som uttrycks med "eller", och exklusiv disjunktion eller stark disjunktion, som uttrycks med "antingen eller".
Påståendet, p eller q, är sant om minst en av p och q är sann och påståendet, antingen p eller q, är sant om exakt en av p och q är sann.
Det finns många skillnader mellan normal användning av "eller" i talspråket och motsvarande operator i satslogiken. Ofta förutsätts någon form av naturligt eller rimligt samband mellan leden i disjunktionen i talspråket.
I satsen: "Te eller kaffe serveras efter desserten", uppfattas disjunktionen som stark medan den i satsen: "Pensionärer eller barn har fri entré", uppfattas som svag.
Representation
[redigera | redigera wikitext]Inklusiv disjunktion betecknas med och exklusiv disjunktion med . I boolesk algebra betecknas inklusiv disjunktion med . Exklusiv disjunktion har i den booleska algebran ingen distinkt symbol, men betecknas i andra sammanhang med , vilket står för räkning modulo-2.
När inte symbolen är tillgänglig skrivs den ibland ut som XOR. I programmeringsspråken Java, C och C++ används insättningstecknet (alltså ^).
Sanningsfunktion och sanningstabell
[redigera | redigera wikitext]Disjunktionens egenskaper beskrivs i logiken som en funktion – en sanningsfunktion – av de ingående påståendenas sanningsvärden. Detta beskrivs med sanningstabeller, där F = falsk och S = sann:
|
|
Boolesk algebra
[redigera | redigera wikitext]I boolesk algebra skrivs inklusiv disjunktion och exklusiv disjunktion enligt
- p eller q = p + q
- Antingen p eller q = p · q ' + p ' · q, där p ' och q ' är inverserna till p respektive q.
Med talen 0 för falsk och 1 för sann och de booleska reglerna 1 + 1 = 1 och 1 ⊕ 1 = 0 fås tabellerna
|
|
I en variant av boolesk algebra, där minustecknet införts och där vanliga räkneregler gäller, det vill säga utan specialregler för de matematiska operationerna + och ·, beskrivs de två disjunktionerna med sanningsfunktionerna
- p OR q = p + q - p·q
- p XOR q = p + q - 2·p·q
med egenskaper enligt tabellerna
|
|
Tekniska lösningar
[redigera | redigera wikitext]I elektriska kretsar, pneumatik, hydraulik, mekanik etcetera kan funktioner som motsvarar disjunktioner realiseras, som i kombination med andra logiska funktioner kan byggas ihop till komplex funktionalitet. Några exempel:
Parallellkoppling
[redigera | redigera wikitext]Om till exempel två parallellkopplade brytare seriekopplas med en lampa måste båda brytarna vara från för att lampan ska vara släckt; i annat fall tänds lampan. Detta realiserar en inklusiv disjunktion.

Trappomkastare
[redigera | redigera wikitext]En korsad trappomkastare realiserar en exklusiv disjunktion (se bild).

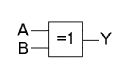
OR-grind och XOR-grind
[redigera | redigera wikitext]I digitaltekniken realiseras samma funktioner med logiska byggblock, OR-grind respektive XOR-grind. "Värdena" är här signalena "hög" och "låg" som motsvarar bestämda spänningsintervall. Dessa betecknas vanligen med 1 = hög och 0 = låg.
 | 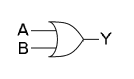 |
|
 | 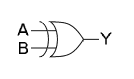 |
|
Ett integrerat kretsblock som tillhandahåller OR-grindar är till exempel 7432 som innehåller fyra separata grindar. 74386 innehåller fyra separata XOR-grindar.
Spelteori
[redigera | redigera wikitext]Inom spelteori, heter XOR nim-summa och betecknas , från att den används i analys av spelet Nim.
Referenser
[redigera | redigera wikitext]- Karl-Johan Bäckström, Diskret matematik, Studentlitteratur, Lund 1986.
- Raymond M Smullyan, First-Order Logic, Springer-Verlag, Berlin Heidelberg, New York, 1968.
- Elliott Mendelson, Elementary Logic, Oxford University Press, London 1965.
- Göran Hermerén, Satslogik, Studentlitteratur, Lund 1967.
- Per-Erik Danielsson, Digital teknik, Studentlitteratur, Lund 1974.


 French
French Deutsch
Deutsch





