Tangens hyperbolicus – Wikipedia

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2025-06) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

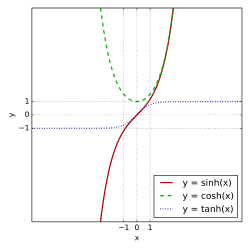
Tangens hyperbolicus eller tanh är en hyperbolisk funktion. Den är den hyperboliska mostvarigheten till tangensfunktionen. Tanh är en udda funktion.

Definition:

${\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}$

Derivatan av tanh:

${\displaystyle {\frac {d}{dx}}\tanh(x)=1-\tanh ^{2}(x)\,}$

Tangens hyperbolicus har en äkta invers, arctanh:

${\displaystyle \tanh ^{-1}\,z={\frac {1}{2}}\ln {\frac {1+z}{1-z}}.}$