Dünya'nın yörüngesi - Vikipedi

Dünya, Kuzey Yarımküre'den bakıldığında saat yönünün tersine doğru ortalama 149,60 milyon km (92,96 milyon mil)^[1] mesafede Güneş'in çevresinde dönmektedir. Bir tam yörünge 365.256 gün (1 yıldız yılı) sürer ve bu süre zarfında Dünya 940 milyon km (584 milyon mil) yol kat etmiş olur.^[2] Diğer Güneş Sistemi cisimlerinin etkisi göz ardı edildiğinde, Dünya'nın yörüngesi, Dünya'nın dönüşü olarak da bilinir. Dünya'nın dışmerkezliği 0,0167'dir. Bu nedenle Dünya-Güneş ağırlık merkezi odaklı, çift merkezli bir elipstir. Yörünge merkezi, yörüngenin büyüklüğüne göre Güneş'in merkezine nispeten yakın olduğundan, bu değer sıfıra yakındır.

Dünya'dan bakıldığında, gezegenin doğrusal yörünge hareketi, Güneş'in diğer yıldızlara göre her bir güneş gününde yaklaşık 1° doğuya doğru (ya da her 12 saatte bir Güneş veya Ay çapı kadar) hareket ediyormuş gibi görünmesine neden olur.^{[nb 1]} Dünya'nın yörünge hızı ortalama 29,78 km/s (107.208 km/h; 66.616 mph) olup, gezegenin çapını 7 dakikada ve Ay'a olan mesafeyi ise 4 saatte kat edecek kadar hızlıdır.^[3]

Güneş'in ya da Dünya'nın kuzey kutbunun üzerindeki bir noktadan bakıldığında, Dünya Güneş'in etrafında saat yönünün tersine dönüyor gibi görünmektedir. Aynı bakış açısından, hem Dünya hem de Güneş kendi eksenleri etrafında saat yönünün tersine dönüyor gibi görünür.

Çalışma tarihi

Günmerkezlilik, ilk olarak Güneş'i Güneş Sistemi'nin merkezine yerleştiren ve Dünya da dahil olmak üzere diğer gezegenleri onun yörüngesine oturtan bir bilimsel modeldir. Tarihsel olarak bakıldığında "heliosentrizm", Dünya'yı merkeze yerleştiren "geosentrizme" karşıttır. Sisamlı Aristarkus MÖ üçüncü yüzyılda güneş merkezli bir model önermiştir. On altıncı yüzyılda Nicolaus Copernicus'un "De revolutionibus" adlı kitabı, tıpkı Batlamyus'un ikinci yüzyılda yermerkezli modelini sunduğu gibi, güneşmerkezli bir evren modelinin^[4] tam bir tartışmasını sunmuştur. Bu "Kopernik Devrimi" gezegenlerin görünen geriye doğru hareketi meselesini, bu tür bir hareketin yalnızca algılanan ve görünen bir şey olduğunu savunarak çözüme kavuşturmuştur. Tarihçi Jerry Brotton'a göre, "Kopernik'in çığır açan kitabı... bir yüzyıldan fazla bir süre önce [basılmış] olmasına rağmen, [Hollandalı haritacı] Joan Blaeu onun devrimci güneş merkezli teorisini bir dünya haritasına dahil eden ilk haritacı olmuştur."^[5]

Dünya'ya olan etkisi

Dünya'nın eksen eğikliği nedeniyle, Güneş'in yörüngesinin gökyüzündeki eğimi yıl boyunca değişir. Kuzey enlemindeki bir gözlemci için kuzey kutbu Güneş'e doğru eğildiğinde gün daha uzun sürer ve Güneş gökyüzünde daha yüksekte görünür. Bu da yüzeye daha fazla güneş radyasyonu ulaştığı için ortalama sıcaklıkların yükselmesine neden olur. Kuzey kutbu Güneş'ten uzağa doğru eğildiğinde ise bunun tam tersi geçerlidir ve hava genellikle daha soğuktur. Kuzey Kutup Dairesi'nin kuzeyinde ve Antarktika Dairesi'nin güneyinde, yılın bir bölümünde hiç gün ışığının olmadığı ve yılın diğer zamanlarında sürekli gün ışığının olduğu aşırı bir duruma ulaşılır. Bu durumlara sırasıyla kutup gecesi ve gece yarısı güneşi denir. Hava durumundaki bu değişim mevsimlerle sonuçlanır.^[6]

Yörünge olayları

Astronomik geleneklere göre, dört mevsim gündönümleri (Dünya'nın yörüngesinde, Dünya'nın ekseninin Güneş'e doğru veya Güneş'ten uzağa maksimum eğiminin olduğu iki nokta) ve ekinokslar (Dünya'nın yörüngesinde, Dünya'nın eğik ekseni ile Dünya'dan Güneş'e çizilen hayali bir çizginin birbirine tam olarak dik olduğu iki nokta) tarafından belirlenir. Gündönümleri ve ekinokslar yılı yaklaşık olarak dört eşit parçaya böler. Kuzey yarımkürede kış gündönümü 21 Aralık veya civarında; yaz gündönümü 21 Haziran civarında; ilkbahar ekinoksu 20 Mart civarında ve sonbahar ekinoksu 23 Eylül civarında gerçekleşir.^[7] Dünya'nın güney yarımküredeki eksen eğikliğinin etkisi kuzey yarımküredekinin tersidir, dolayısıyla güney yarımküredeki gündönümü ve ekinoks mevsimleri kuzey yarımküredekilerin tersidir (örneğin kuzey yaz gündönümü güney kış gündönümü ile aynı zamanda gerçekleşir).

Günümüzde Dünya'nın enberisi 3 Ocak, enötesi ise 4 Temmuz civarında gerçekleşmektedir. Başka bir deyişle, Dünya Ocak ayında Güneş'e daha yakın, Temmuz ayında ise daha uzaktır; bu durum, Dünya'nın Güneş'e en yakın olduğu zamanlarda daha soğuk, en uzak olduğu zamanlarda ise daha sıcak olan kuzey yarımkürede yaşayanlar için mantığa aykırı görünebilir. Değişen Dünya-Güneş mesafesi, enöteye göre enberide Dünya'ya ulaşan toplam güneş enerjisinde yaklaşık %7'lik bir artışa neden olmaktadır.^[8] Güney yarımküre, Dünya'nın Güneş'e en yakın olduğu zamanda Güneş'e doğru eğildiğinden, güney yarımküre bir yıl boyunca Güneş'ten kuzey yarımküreye göre biraz daha fazla enerji almaktadır. Ancak bu etki, eksen eğikliğinden kaynaklanan toplam enerji değişiminden çok daha az önemlidir ve fazla enerjinin çoğu güney yarımkürede suyla kaplı daha yüksek yüzey oranı tarafından emilir.^[9]

Dünya'nın Hill küresi (yerçekimsel etki alanı) yaklaşık 1.500.000 kilometre (0,01 AU) yarıçapındadır veya Ay'a olan ortalama uzaklığın yaklaşık dört katıdır.^[10]^{[nb 2]} Bu, Dünya'nın yerçekimsel etkisinin daha uzaktaki Güneş ve gezegenlerden daha güçlü olduğu maksimum mesafedir. Dünya'nın yörüngesindeki nesneler bu yarıçap içinde olmalıdır, aksi takdirde Güneş'in kütleçekimsel pertürbasyonuyla serbest kalabilirler.

Yörünge özellikleri
epoch	J2000.0^{[nb 3]}
aphelion	15.210×10^⁶ km (9.450×10^⁶ mi)1.0167 AU^{[nb 4]}
perihelion	14.710×10^⁶ km (9.140×10^⁶ mi)0.98329 AU^{[nb 4]}
yarı büyük eksen	14.960×10^⁶ km (9.300×10^⁶ mi)1.0000010178 AU^[11]
dışmerkezlik	0.0167086^[11]
yörünge eğikliği	Güneş'in ekvatoruna 7.155° değişmez düzleme göre 1.578690°^[12]
çıkış düğümü boylamı	174.9°^[11]
enberi boylamı	102.9°^[11]
enberi açısı	288.1°^[11]^{[nb 5]}
yörünge periyodu	365.256363004 days^[13]
ortalama yörünge hızı	2.978 km/s (1.850 mi/s)^[3]107.208 km/sa (66.616 mph)
enöte hızı	2.929 km/s (1.820 mi/s)^[3]
enberi hızı	3.029 km/s (1.882 mi/s)^[3]

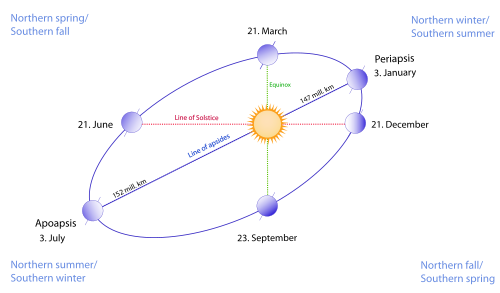
Dünya'nın Güneş etrafındaki eliptik yörüngesinin abartılı çizimi, yörüngedeki uç noktaların (apoapsis ve periapsis) dört mevsimsel uç noktayla (ekinoks ve gündönümü) aynı olmadığını göstermektedir.

Yandaki diyagram gündönümü çizgisi ile Dünya'nın eliptik yörüngesinin apsis çizgisi arasındaki ilişkiyi göstermektedir.

Yörünge elipsi altı Dünya görüntüsünün her birinden geçmektedir.

Bunlar sırayla;

perihelion (periapsis-Güneş'e en yakın nokta) 2-5 Ocak tarihleri arasında herhangi bir yerde,
Mart ekinoksunun 19, 20 veya 21 Mart'taki noktası,
Haziran gündönümünün 20, 21 veya 22 Haziran'daki noktası,
Aphelion (apoapsis-Güneş'ten en uzak nokta) 3 Temmuz ile 5 Temmuz arasında herhangi bir tarihte,
Eylül ekinoksu 22, 23 veya 24 Eylül'de,
ve 21, 22 veya 23 Aralık'ta Aralık gündönümünü

göstermektedir.^[7] Dünya'nın gerçek yörüngesi, diyagramda gösterildiği gibi olmayıp, neredeyse daireseldir.

Geleceği

Matematikçiler ve astronomlar (Laplace, Lagrange, Gauss, Poincaré, Kolmogorov, Vladimir Arnold ve Jürgen Moser gibi) gezegen hareketlerinin kararlılığına dair kanıtlar aramış ve bu arayış birçok matematiksel gelişmeye ve Güneş Sistemi için birbirini izleyen birkaç kararlılık "kanıtına" yol açmıştır.^[14] Çoğu tahmine göre, Dünya'nın yörüngesi uzun süreler boyunca nispeten kararlı olacaktır.^[15]

1989 yılında Jacques Laskar'ın çalışması, Dünya'nın yörüngesinin (ve tüm iç gezegenlerin yörüngelerinin) kaotik hale gelebileceğini ve bugün Dünya'nın başlangıç konumunu ölçerken 15 metre kadar küçük bir hatanın, Dünya'nın 100 milyon yıldan biraz daha uzun bir süre sonra yörüngesinde nerede olacağını tahmin etmeyi imkansız hale getireceğini göstermiştir.^[16] Güneş Sisteminin modellenmesi, n-cisim probleminin kapsadığı bir konudur.

Ayrıca bakınız

Notlar

^ Gezegenimizin Güneş'in etrafındaki dönüşü yaklaşık 365 gün sürer. Tam bir yörünge ise 360°'dir. Bu durum, Dünya'nın kendi yörüngesinde her gün yaklaşık 1 derecelik bir yol kat ettiğini göstermektedir. Dolayısıyla, Güneş de yıldızlara göre gökyüzünde aynı miktarda hareket ediyor gibi görünecektir.
^ Dünya için Hill yarıçapı
$R_{H}=a\left({\frac {m}{3M}}\right)^{1/3},$ m burada Dünya'nın kütlesi, a Astronomik Birim ve M ise Güneş'in kütlesini göstermektedir. Bu nedenle, yarıçap $\left({\frac {1}{3\cdot 332\,946}}\right)^{1/3}\approx 0.01$ şeklinde hesaplanmaktadır.
^ Tüm astronomik büyüklükler hem seküler hem de periyodik olarak değişir. Verilen nicelikler, tüm periyodik varyasyonları göz ardı ederek, seküler varyasyonun J2000.0 andaki değerleridir.
^ ^a ^b enöte= a × (1 + e); enberi = a × (1 – e), burada a yarı büyük ekseni ve e dışmerkezliği belirtir.
^ Referans, yükselen düğümün boylamı ile enberi argümanının toplamı olan enberi boylamını vermektedir. Bundan (102.937°) 174.873°'lik düğüm boylamını çıkarırsak -71.936° elde ederiz. 360° eklendiğinde 288.064° elde edilir. Bu ekleme açıyı değiştirmez, ancak boylamlar için olağan 0-360° aralığında bir değer ifade eder.

Kaynaklar

^ "Sun: Facts & Figures". Solar System Exploration. National Aeronautics and Space Administration. July 3, 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: July 29, 2015.
^ Jean Meeus, Astronomical Algorithms 2nd ed, 0-943396-61-1 (Richmond, VA: Willmann-Bell, 1998) 238.
^ ^a ^b ^c ^d Williams, David R. (1 Eylül 2004). "Earth Fact Sheet". NASA. 19 Aralık 1996 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Mart 2007.
^ De revolutionibus orbium coelestium. Johannes Petreius. 1543.
^ Jerry Brotton, A History of the World in Twelve Maps, London: Allen Lane, 2012, 9781846140990 p. 262.
^ "What causes the seasons? (NASA)". 19 Şubat 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Ocak 2015.
^ ^a ^b "Date & Time of Solstices & Equinoxes". 28 Ağustos 2013. 19 Ocak 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Ocak 2015.
^ "Solar Energy Reaching The Earth's Surface". ITACA. 30 Ocak 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 30 Ocak 2022.
^ Williams, Jack (20 Aralık 2005). "Earth's tilt creates seasons". USAToday. 29 Şubat 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Mart 2007.
^ Vázquez, M.; Montañés Rodríguez, P.; Palle, E. (2006). "The Earth as an Object of Astrophysical Interest in the Search for Extrasolar Planets" (PDF). Instituto de Astrofísica de Canarias. 14 Haziran 2007 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 21 Mart 2007.
^ ^a ^b ^c ^d ^e Simon, J.L.; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (February 1994). "Numerical expressions for precession formulae and mean elements for the Moon and planets". Astronomy and Astrophysics. 282 (2): 663-683. Bibcode:1994A&A...282..663S.
^ Allen, Clabon Walter; Cox, Arthur N. (2000). Allen's Astrophysical Quantities. Springer. s. 294. ISBN 0-387-98746-0. 21 Şubat 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Ağustos 2023.
^ The figure appears in multiple references, and is derived from the VSOP87 elements from section 5.8.3, p. 675 of the following: Simon, J. L.; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (February 1994). "Numerical expressions for precession formulae and mean elements for the Moon and planets". Astronomy and Astrophysics. 282 (2): 663-683. Bibcode:1994A&A...282..663S.
^ Laskar, J. (2001). "Solar System: Stability". Murdin, Paul (Ed.). Encyclopedia of Astronomy and Astropvhysics. Bristol: Institute of Physics Publishing. article 2198.
^ Gribbin, John (2004). Deep simplicity : bringing order to chaos and complexity (1. U.S. bas.). New York: Random House. ISBN 978-1-4000-6256-0.
^ "Earth-Venus smash-up possible". 11 Haziran 2009. 23 Ocak 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Ocak 2015.

Dış bağlantılar

Wikimedia Commons'ta Dünya'nın yörüngesi ile ilgili ortam dosyaları bulunmaktadır.

Earth – Speed through space – about 1 million miles an hour 5 Nisan 2021 tarihinde Wayback Machine sitesinde arşivlendi. – NASA

[3] Gezegenimizin Güneş'in etrafındaki dönüşü yaklaşık 365 gün sürer. Tam bir yörünge ise 360°'dir. Bu durum, Dünya'nın kendi yörüngesinde her gün yaklaşık 1 derecelik bir yol kat ettiğini göstermektedir. Dolayısıyla, Güneş de yıldızlara göre gökyüzünde aynı miktarda hareket ediyor gibi görünecektir.

[12] Dünya için Hill yarıçapı
$R_{H}=a\left({\frac {m}{3M}}\right)^{1/3},$ m burada Dünya'nın kütlesi, a Astronomik Birim ve M ise Güneş'in kütlesini göstermektedir. Bu nedenle, yarıçap $\left({\frac {1}{3\cdot 332\,946}}\right)^{1/3}\approx 0.01$ şeklinde hesaplanmaktadır.

[epoch-13] Tüm astronomik büyüklükler hem seküler hem de periyodik olarak değişir. Verilen nicelikler, tüm periyodik varyasyonları göz ardı ederek, seküler varyasyonun J2000.0 andaki değerleridir.

[apsis-14] öte= a × (1 + e); enberi = a × (1 – e), burada a yarı büyük ekseni ve e dışmerkezliği belirtir.

[arg_peri-17] Referans, yükselen düğümün boylamı ile enberi argümanının toplamı olan enberi boylamını vermektedir. Bundan (102.937°) 174.873°'lik düğüm boylamını çıkarırsak -71.936° elde ederiz. 360° eklendiğinde 288.064° elde edilir. Bu ekleme açıyı değiştirmez, ancak boylamlar için olağan 0-360° aralığında bir değer ifade eder.

[1] "Sun: Facts & Figures". Solar System Exploration. National Aeronautics and Space Administration. July 3, 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: July 29, 2015.

[AA-2] Jean Meeus, Astronomical Algorithms 2nd ed, 0-943396-61-1 (Richmond, VA: Willmann-Bell, 1998) 238.

[earth_fact_sheet-4] Williams, David R. (1 Eylül 2004). "Earth Fact Sheet". NASA. 19 Aralık 1996 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Mart 2007.

[5] De revolutionibus orbium coelestium. Johannes Petreius. 1543.

[6] Jerry Brotton, A History of the World in Twelve Maps, London: Allen Lane, 2012, 9781846140990 p. 262.

[7] "What causes the seasons? (NASA)". 19 Şubat 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Ocak 2015.

[:0-8] "Date & Time of Solstices & Equinoxes". 28 Ağustos 2013. 19 Ocak 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Ocak 2015.

[9] "Solar Energy Reaching The Earth's Surface". ITACA. 30 Ocak 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 30 Ocak 2022.

[10] Williams, Jack (20 Aralık 2005). "Earth's tilt creates seasons". USAToday. 29 Şubat 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Mart 2007.

[11] Vázquez, M.; Montañés Rodríguez, P.; Palle, E. (2006). "The Earth as an Object of Astrophysical Interest in the Search for Extrasolar Planets" (PDF). Instituto de Astrofísica de Canarias. 14 Haziran 2007 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 21 Mart 2007.

[VSOP87-15] Simon, J.L.; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (February 1994). "Numerical expressions for precession formulae and mean elements for the Moon and planets". Astronomy and Astrophysics. 282 (2): 663-683. Bibcode:1994A&A...282..663S.

[Allen294-16] Allen, Clabon Walter; Cox, Arthur N. (2000). Allen's Astrophysical Quantities. Springer. s. 294. ISBN 0-387-98746-0. 21 Şubat 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Ağustos 2023.

[18] The figure appears in multiple references, and is derived from the VSOP87 elements from section 5.8.3, p. 675 of the following: Simon, J. L.; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (February 1994). "Numerical expressions for precession formulae and mean elements for the Moon and planets". Astronomy and Astrophysics. 282 (2): 663-683. Bibcode:1994A&A...282..663S.

[19] Laskar, J. (2001). "Solar System: Stability". Murdin, Paul (Ed.). Encyclopedia of Astronomy and Astropvhysics. Bristol: Institute of Physics Publishing. article 2198.

[20] Gribbin, John (2004). Deep simplicity : bringing order to chaos and complexity (1. U.S. bas.). New York: Random House. ISBN 978-1-4000-6256-0.

[21] "Earth-Venus smash-up possible". 11 Haziran 2009. 23 Ocak 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Ocak 2015.

[1]

[2]

[nb 1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[nb 2]

[nb 3]

[nb 4]

[11]

[12]

[nb 5]

[13]

[14]

[15]

[16]

g t d Dünya
Kıtalar	Afrika Antarktika Asya Avrupa Avustralya Güney Amerika Kuzey Amerika	Dünya
Okyanuslar	Arktik Okyanusu Atlas Okyanusu Büyük Okyanus Güney Okyanusu Hint Okyanusu
Coğrafyası ve jeolojisi	Dünya'nın enleri Dünya'nın yaşı Gelecek Jeofizik Jeoloji Jeolojik kayıt Jeolojik tarih zaman cetveli Levha tektoniği Manyetik alan Yapı Yerçekimi Yer bilimleri Yerküre tarihi
Atmosfer	Dünya atmosferi Hava durumu İklim İklim değişikliği
Çevre	Biyom Biyosfer Doğa Ekoloji Ekosistem İnsanın çevre üzerindeki etkisi Yaşamın evrimsel tarihi zaman çizelgesi
Kartografya	Dijital haritalandırma Dünya haritası Sanal yerküre Uydu görüntüleri
Kültür ve toplum	Etimoloji Dünya ekonomisi Dünya Günü Dünya toplumu Kültürde dünya İnsanlık tarihi Ülkeler Zaman dilimi
Gezegen bilimi	Ay Dünya'nın iddia edilen uyduları Dünya'nın konumu Dünya'nın yörüngesi Güneş Sistemi Güneş Sistemi'nin oluşumu ve evrimi Güneş Sistemi yörüngesindeki karasal gezegenlerin jeolojisi Kordylewski bulutu Tutulum
Kategori