French
DeutschDosya:Standard symmetric pdfs logscale.svg - Vikipedi
Bu SVG dosyasının PNG önizlemesinin boyutu: 400 × 300 piksel. Diğer çözünürlükler: 320 × 240 piksel | 640 × 480 piksel | 1.024 × 768 piksel | 1.280 × 960 piksel | 2.560 × 1.920 piksel.
Tam çözünürlük (SVG dosyası, sözde 400 × 300 piksel, dosya boyutu: 235 KB)
 | Bu dosya Wikimedia Commons'ta bulunmaktadır. Dosyanın açıklaması aşağıda gösterilmiştir. Commons, serbest/özgür telifli medya dosyalarının bulundurulduğu depodur. Siz de yardım edebilirsiniz. |
Özet
| Açıklama | English: Logscale plot of several symmetric unimodal probability densities with unit variance. From highest to lowest peak: red, kurtosis 3, Laplace (D)ouble exponential distribution; orange, kurtosis 2, hyperbolic (S)ecant distribution; green, kurtosis 1.2, (L)ogistic distribution; black, kurtosis 0, (N)ormal distribution; cyan, kurtosis −0.593762…, raised (C)osine distribution; blue, kurtosis −1, (W)igner semicircle distribution; magenta, kurtosis −1.2, (U)niform distribution. | ||||||
| Tarih | |||||||
| Kaynak | MarkSweep | ||||||
| Yazar | Vektör: | ||||||
| İzin (Bu dosyanın tekrar kullanımı) |
Ben, bu işin telif sahibi, burada işi aşağıdaki lisans altında yayımlıyorum:
| ||||||
| Diğer sürümler | File:Standard symmetric pdfs.svg File:Standard symmetric pdfs.png File:Standard symmetric pdfs logscale.png | ||||||
| SVG gelişimi |  Bu SVG kaynak kodu geçerlidir.  Bu vektörel grafik Gnuplot ile oluşturuldu. | ||||||
| Kaynak kodu |
# Laplace double exponential distribution, kurtosis 3 laplace(x) = exp(-abs(x)*sqrt(2)) * sqrt(0.5) # sech distribution, kurtosis 2 sech(x) = 2.0 / (exp(x) + exp(-x)) sech_pdf(x) = 0.5 * sech(0.5*pi*x) # logistic distribution, kurtosis 1.2 slogist = sqrt(3) / pi logist(x) = exp(-x/slogist) / slogist / (1 + exp(-x/slogist))**2 # normal distribution, kurtosis 0 n(x) = exp(-0.5*x*x) / sqrt(2*pi) # raised cosine distribution, kurtosis -0.59376 scos = 1.0 / sqrt(1/3.0 - 2/pi**2) cosine(x) = abs(x)>scos? 0 : (1+cos(x*pi/scos))*0.5/scos # Wigner semicircle distribution, kurtosis -1 wigner(x) = abs(x)>2? 0 : sqrt(4-x*x)*0.5/pi # uniform distribution, kurtosis -1.2 uniform(x) = abs(x)>sqrt(3)? 0 : 0.5/sqrt(3) set samples 6001 set grid set xrange [-10.4:10.4] set logscale y set yrange [1e-24:5] set ytics 1e3 set key right bottom font ",8" enhanced set terminal svg size 400,300 enhanced fname 'DejaVu Sans' fsize 10 butt solid set output 'Standard symmetric pdfs logscale.svg' plot \ laplace(x) lt 1 lw 2 title "D, 3", \ sech_pdf(x) lt 8 lw 2 title "S, 2", \ logist(x) lt 2 lw 2 title "L, 1.2", \ n(x) lt 7 lw 2 title "N, 0", \ cosine(x) lt 5 lw 2 title "C, -0.59376", \ wigner(x) lt 3 lw 2 title "W, -1", \ uniform(x) lt 4 lw 2 title "U, -1.2" |
Dosya geçmişi
Dosyanın herhangi bir zamandaki hâli için ilgili tarih/saat kısmına tıklayın.
| Tarih/Saat | Küçük resim | Boyutlar | Kullanıcı | Yorum | |
|---|---|---|---|---|---|
| güncel | 16.07, 26 Mayıs 2020 | 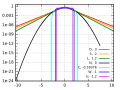| 400 × 300 (235 KB) | Andel | == {{int:filedesc}} == {{Information |description=|Description= {{en|1=Logscale plot of several symmetric unimodal probability densities with unit variance. From highest to lowest peak: {{Legend|red|red, kurtosis 3, Laplace (D)ouble exponential distribution;}} {{Legend|orange|orange, kurtosis 2, hyperbolic (S)ecant distribution;}} {{Legend|green|green, kurtosis 1.2, (L)ogistic distribution;}} {{Legend|... |
Dosya kullanımı
Bu görüntü dosyasına bağlantısı olan sayfalar:
Küresel dosya kullanımı
Aşağıdaki diğer vikiler bu dosyayı kullanır:
