Nusselt sayısı - Vikipedi

Termal akışkan dinamiği alanında, Nusselt sayısı (Nu), Wilhelm Nusselt'in adını taşıyan ve bir sınır tabakasındaki toplam ısı transferinin, kondüksiyon ısı transferine oranını ifade eden bir boyutsuz sayıdır. Toplam ısı transferi, kondüksiyon ve konveksiyonu içerir. Konveksiyon ise adveksiyon ve difüzyon bileşenlerinden oluşur. Kondüktif bileşen, konvektif koşullar altında ancak hareketsiz bir akışkan için varsayılarak ölçülür. Nusselt sayısı, akışkanın Rayleigh sayısı ile yakından ilişkilidir.^[1]:466

Nusselt sayısının bir büyüklüğündeki mertebesi, saf kondüksiyonla ısı transferini temsil ederken, bir ile 10 arasındaki değerler tıkız akış (İng. slug flow) veya laminer akışa özgüdür.^[2] Daha yüksek Nusselt sayıları daha aktif konveksiyon anlamına gelir ve türbülanslı akış genellikle 100-1000 aralığında bulunur.^[2]

Benzer şekilde, Biot sayısı katı cisimler için ısı iletkenliğini ele alırken, Nusselt sayısının kütle transferi karşılığı Sherwood sayısıdır.

Nusselt sayısı, bir sınır tabakası boyunca toplam ısı transferinin (kondüksiyon + konveksiyon) kondüksiyon ısı transferine oranıdır. Konveksiyon ve kondüksiyon ısı akışları, sınır tabakası yüzeyinin normaline paralel olup, ortalama akışkan akışına dik olarak gerçekleşir.

${\displaystyle \mathrm {Nu} _{L}={\frac {\mbox{Toplam ısı transferi }}{\mbox{Kondüksiyon ısı transferi }}}={\frac {h}{k/L}}={\frac {hL}{k}}}$

Burada h, akışın konvektif ısı transferi katsayısını, L karakteristik uzunluğu ve k akışkanın ısı iletkenliğini temsil eder.

• Karakteristik uzunluğun seçimi, sınır tabakasının büyüme veya kalınlık yönünde olmalıdır; karakteristik uzunluk örnekleri şunlardır: silindirin eksenine dik olarak çapraz akışta (İng. cross flow) bir silindirin dış çapı, doğal konveksiyona maruz kalan dikey bir plakanın uzunluğu veya bir kürenin çapı. Karmaşık geometriler için uzunluk, akışkan cismin hacminin yüzey alanına bölünmesiyle tanımlanabilir.
• Akışkanın ısı iletkenliği genellikle film sıcaklığında değerlendirilir ve mühendislik uygulamaları için bu, yığın (İng. bulk) akışkan sıcaklığı ile duvar yüzey sıcaklığının aritmetik ortalaması olarak hesaplanabilir.

Yukarıda verilen tanımın aksine, "ortalama Nusselt sayısı" olarak bilinen yerel Nusselt sayısı, uzunluğun yüzey sınırından^[1] ilgi noktasına olan mesafe olarak alınmasıyla tanımlanır.

${\displaystyle \mathrm {Nu} _{x}={\frac {h_{x}x}{k}}}$

"Olağan" ya da "ortalama" Nusselt sayısı, ilgi alanı boyunca bu ifadenin entegrasyonu ile elde edilir, örneğin:^[3]

${\displaystyle {\overline {\mathrm {Nu} }}={\frac {{\frac {1}{L}}\int _{0}^{L}h_{x}\ dx\ L}{k}}={\frac {{\overline {h}}L}{k}}}$

Bir yüzey ile üzerinden akışkan akan bir akışkan arasında konvektif ısı transferini anlamak için konveksiyon sınır tabakalarının anlaşılması gereklidir. Akışkan serbest akım sıcaklığı ile yüzey sıcaklıkları farklı olduğunda bir termal sınır tabakası oluşur. Bu sıcaklık farkından kaynaklanan enerji değişimi nedeniyle bir sıcaklık profili ortaya çıkar.

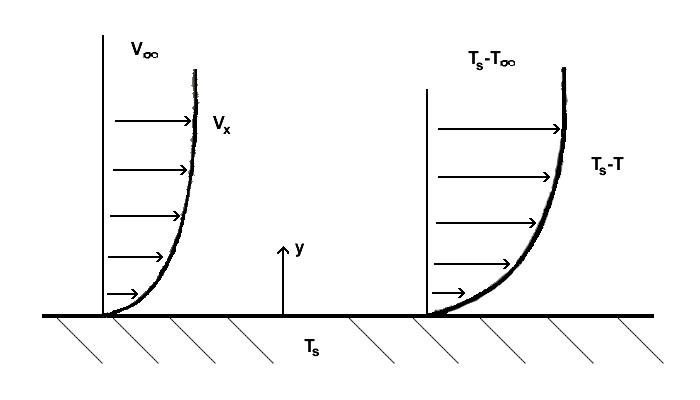
Isı transfer oranı, Newton soğuma yasası kullanılarak şu şekilde ifade edilebilir:

${\displaystyle Q_{y}=hA\left(T_{s}-T_{\infty }\right)}$,

burada h ısı transfer katsayısı ve A ısı transfer yüzey alanıdır. Yüzeydeki ısı transferi iletim yoluyla gerçekleştiğinden, aynı miktar ısı iletkenliği k cinsinden şu şekilde ifade edilebilir:

${\displaystyle Q_{y}=-kA{\frac {\partial }{\partial y}}\left.\left(T-T_{s}\right)\right|_{y=0}}$.

Bu iki terim eşittir ve bu nedenle

${\displaystyle -kA{\frac {\partial }{\partial y}}\left.\left(T-T_{s}\right)\right|_{y=0}=hA\left(T_{s}-T_{\infty }\right)}$.

Bu ifadeyi yeniden düzenleyerek,

${\displaystyle {\frac {h}{k}}={\frac {\left.{\frac {\partial \left(T_{s}-T\right)}{\partial y}}\right|_{y=0}}{\left(T_{s}-T_{\infty }\right)}}}$.

Temsili bir uzunluk L ile çarptığımızda boyutsuz bir ifade elde ederiz:

${\displaystyle {\frac {hL}{k}}={\frac {\left.{\frac {\partial \left(T_{s}-T\right)}{\partial y}}\right|_{y=0}}{\frac {\left(T_{s}-T_{\infty }\right)}{L}}}}$.

Sağ taraf artık yüzeydeki sıcaklık gradyanının referans sıcaklık gradyanına oranını temsil ederken, sol taraf Biot modülüne benzer. Bu ifade, iletken termal direncin, akışkanın konvektif termal direncine oranı olan Nusselt sayısı, Nu olarak bilinir.

${\displaystyle \mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}}$.

Nusselt sayısı, Fourier kanununun boyutsuz bir analizi ile elde edilebilir çünkü bu sayı, yüzeydeki boyutsuz sıcaklık gradyanına eşittir:

${\displaystyle q=-kA\nabla T}$, burada q ısı akımı, k sabit ısı iletkenliği ve T akışkan sıcaklığıdır.

Eğer: ${\displaystyle \nabla '=L\nabla }$ ve ${\displaystyle T'={\frac {T-T_{h}}{T_{h}-T_{c}}}}$ olursa,

şuraya varırız:

${\displaystyle -\nabla 'T'={\frac {L}{kA(T_{h}-T_{c})}}q={\frac {hL}{k}}}$

sonra aşağıdaki tanımlamayı yapabiliriz:

${\displaystyle \mathrm {Nu} _{L}={\frac {hL}{k}}}$

bu nedenle denklem şu hale gelir:

${\displaystyle \mathrm {Nu} _{L}=-\nabla 'T'}$

Cismin yüzeyi üzerinde entegrasyon yaparak aşağıdaki sonucu elde edebiliriz:

${\displaystyle {\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!}$,

burada ${\displaystyle S'={\frac {S}{L^{2}}}}$'dir.

Genellikle doğal konveksiyon (zorlanmamış konveksiyon; İng. free convection) için, ortalama Nusselt sayısı Rayleigh sayısı ve Prandtl sayısının bir fonksiyonu olarak ifade edilir ve şu şekilde yazılır:

${\displaystyle \mathrm {Nu} =f(\mathrm {Ra} ,\mathrm {Pr} )}$

Zorlanmış konveksiyon durumunda ise, Nusselt sayısı genellikle Reynolds sayısı ve Prandtl sayısının bir fonksiyonu olarak ifade edilir:

${\displaystyle \mathrm {Nu} =f(\mathrm {Re} ,\mathrm {Pr} )}$

Churchill ve Chu'dan alıntılanmıştır^[4]:493:

${\displaystyle {\overline {\mathrm {Nu} }}_{L}\ =0.68+{\frac {0.663\,\mathrm {Ra} _{L}^{1/4}}{\left[1+(0.492/\mathrm {Pr} )^{9/16}\,\right]^{4/9}\,}}\quad \mathrm {Ra} _{L}\leq 10^{8}}$

Eğer karakteristik uzunluk şu şekilde tanımlanırsa

${\displaystyle L\ ={\frac {A_{s}}{P}}}$

burada ${\displaystyle \mathrm {A} _{s}}$ plakanın yüzey alanı ve ${\displaystyle P}$ çevresidir.

Daha soğuk bir ortamda sıcak bir cismin üst yüzeyi veya daha sıcak bir ortamda soğuk bir cismin alt yüzeyi için^[4]:493

${\displaystyle {\overline {\mathrm {Nu} }}_{L}\ =0.54\,\mathrm {Ra} _{L}^{1/4}\,\quad 10^{4}\leq \mathrm {Ra} _{L}\leq 10^{7}}$

${\displaystyle {\overline {\mathrm {Nu} }}_{L}\ =0.15\,\mathrm {Ra} _{L}^{1/3}\,\quad 10^{7}\leq \mathrm {Ra} _{L}\leq 10^{11}}$

Daha soğuk bir ortamda sıcak bir cismin alt yüzeyi veya daha sıcak bir ortamda soğuk bir cismin üst yüzeyi için^[4]:493

${\displaystyle {\overline {\mathrm {Nu} }}_{L}\ =0.52\,\mathrm {Ra} _{L}^{1/5}\,\quad 10^{5}\leq \mathrm {Ra} _{L}\leq 10^{10}}$

Bejan'dan alıntılanmıştır:^[5]

${\displaystyle {\overline {\mathrm {Nu} }}_{L}\ =0.069\,\mathrm {Ra} _{L}^{1/3}Pr^{0.074}\,\quad 3*10^{5}\leq \mathrm {Ra} _{L}\leq 7*10^{9}}$

Bu denklem "yatay tabakanın yeterince geniş olduğu durumlarda, kısa dikey kenarların etkisinin minimal olması durumunda geçerlidir."

Bu, 1959'da Globe ve Dropkin tarafından ampirik olarak belirlenmiştir:^[6] "Testler, bakır üst ve alt kısımları olan ve yalıtımlı duvarlara sahip silindirik kaplarda yapılmıştır." Kullanılan kaplar yaklaşık 5 inç çapında ve 2 inç yüksekliğindeydi.

Bir düz plaka üzerinde laminer akış için yerel Nusselt sayısı, plakanın kenarından aşağı yönde ${\displaystyle x}$ mesafesinde şu şekilde verilir^[4]:490:

${\displaystyle \mathrm {Nu} _{x}\ =0.332\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3},(\mathrm {Pr} >0.6)}$

Bir düz plaka üzerinde laminer akış için ortalama Nusselt sayısı, plakanın kenarından aşağı yönde ${\displaystyle x}$ mesafesine kadar şu şekilde verilir^[4]:490:

${\displaystyle {\overline {\mathrm {Nu} }}_{x}\ ={2}\cdot 0.332\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3}\ =0.664\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3},(\mathrm {Pr} >0.6)}$

Bazı uygulamalarda, örneğin hava içindeki küresel sıvı damlacıklarının buharlaşması gibi, şu korelasyon kullanılır:^[7]

${\displaystyle \mathrm {Nu} _{D}\ ={2}+0.4\,\mathrm {Re} _{D}^{1/2}\,\mathrm {Pr} ^{1/3}\,}$

Gnielinski'nin türbülanslı boru akışı için korelasyonu:^{[4]:{{{1}}}[8]}

${\displaystyle \mathrm {Nu} _{D}={\frac {\left(f/8\right)\left(\mathrm {Re} _{D}-1000\right)\mathrm {Pr} }{1+12.7(f/8)^{1/2}\left(\mathrm {Pr} ^{2/3}-1\right)}}}$

Burada f, Darcy sürtünme faktörüdür ve Moody çizelgesinden veya Petukhov tarafından geliştirilen korelasyondan elde edilebilir:^[4]:490

${\displaystyle f=\left(0.79\ln \left(\mathrm {Re} _{D}\right)-1.64\right)^{-2}}$

Gnielinski Korelasyonu şu durumlar için geçerlidir:^[4]:490

${\displaystyle 0.5\leq \mathrm {Pr} \leq 2000}$

${\displaystyle 3000\leq \mathrm {Re} _{D}\leq 5\times 10^{6}}$

W.H. McAdams tarafından tanıtılan Dittus–Boelter denklemi (türbülanslı akış için) Nusselt sayısını hesaplamak için bir belirtik fonksiyondur (İng. explicit). Çözülmesi kolaydır ancak akışkan boyunca büyük sıcaklık farkları olduğunda daha az doğrudur. Dittus–Boelter denklemi pürüzsüz borular için uyarlanmıştır, bu nedenle pürüzlü borular (çoğu ticari uygulamada) için dikkatli kullanılmalıdır. Dittus–Boelter denklemi aşağıdaki gibidir:

${\displaystyle \mathrm {Nu} _{D}=0.023\,\mathrm {Re} _{D}^{4/5}\,\mathrm {Pr} ^{n}}$

Burada:

${\displaystyle D}$ dairesel kanalın iç çapıdır

${\displaystyle \mathrm {Pr} }$ Prandtl sayısıdır

${\displaystyle n=0.4}$ akışkan ısıtıldığında ve ${\displaystyle n=0.3}$ akışkan soğutulduğunda kullanılır.^[4]:493

Dittus–Boelter denklemi şu durumlar için geçerlidir^[4]:514

${\displaystyle 0.6\leq \mathrm {Pr} \leq 160}$

${\displaystyle \mathrm {Re} _{D}\gtrsim 10,000}$

${\displaystyle {\frac {L}{D}}\gtrsim 10}$

Dittus–Boelter denklemi, kütlesel akışkan ile ısı transfer yüzeyi arasındaki sıcaklık farklarının minimal olduğu durumlarda iyi bir yaklaşımdır ve denklem karmaşıklığından ve yinelemeli çözümden kaçınır. Ortalama kütlesel akışkan sıcaklığı 20 °C (68 °F) olan suyu, viskozite 10,07×10^-4 Pa.s ve ısı transfer yüzey sıcaklığı 40 °C (104 °F) olan bir durumda (viskozite 6,96×10^-4 Pa.s, viskozite düzeltme faktörü ${\displaystyle ({\mu }/{\mu _{s}})}$ olarak 1.45 elde edilebilir. Bu, ısı transfer yüzey sıcaklığı 100 °C (212 °F) olduğunda (viskozite 2,82×10^-4 Pa.s) 3.57'ye çıkarak Nusselt sayısı ve ısı transfer katsayısı üzerinde önemli bir fark yaratır.

Sieder–Tate korelasyonu türbülanslı akış için bir örtük fonksiyondur (İng. implicit), çünkü sistemi doğrusal olmayan bir sınır değer problemi olarak analiz eder. Sieder–Tate sonucu, kütlesel akışkan ortalama sıcaklığı ile ısı transfer yüzey sıcaklığı arasındaki sıcaklık değişiminden dolayı viskozitedeki (${\displaystyle \mu }$ ve ${\displaystyle \mu _{s}}$) değişikliği dikkate aldığı için daha doğru olabilir. Sieder–Tate korelasyonu normalde yinelemeli bir süreçle çözülür, çünkü Nusselt sayısı değiştikçe viskozite faktörü de değişir.^[9]

${\displaystyle \mathrm {Nu} _{D}=0.027\,\mathrm {Re} _{D}^{4/5}\,\mathrm {Pr} ^{1/3}\left({\frac {\mu }{\mu _{s}}}\right)^{0.14}}$^[4]:493

Burada:

${\displaystyle \mu }$ kütlesel akışkan sıcaklığındaki akışkan viskozitesidir

${\displaystyle \mu _{s}}$ ısı transfer sınır yüzey sıcaklığındaki akışkan viskozitesidir

Sieder–Tate korelasyonu şu durumlar için geçerlidir^[4]:493

${\displaystyle 0.7\leq \mathrm {Pr} \leq 16,700}$

${\displaystyle \mathrm {Re} _{D}\geq 10,000}$

${\displaystyle {\frac {L}{D}}\gtrsim 10}$

Tam gelişmiş iç laminer akışlı uzun borular için Nusselt sayıları sabit bir değere eğilim gösterir.

İç akış için:

${\displaystyle \mathrm {Nu} ={\frac {hD_{h}}{k_{f}}}}$

Burada:

D_h = Hidrolik çap

k_f = akışkanın ısı iletkenliği

h = konvektif ısı transfer katsayısıdır.

Incropera & DeWitt'e göre,^[4]:486-487

${\displaystyle \mathrm {Nu} _{D}=3.66}$

OEIS dizisi bu değeri şu şekilde verir: ${\displaystyle \mathrm {Nu} _{D}=3.6567934577632923619...}$.

Sabit yüzey ısı akısı durumu için,^[4]:486-487

${\displaystyle \mathrm {Nu} _{D}=4.36}$

• Sherwood sayısı (kütle transferi Nusselt sayısı)
• Churchill–Bernstein denklemi
• Biot sayısı
• Reynolds sayısı
• Konvektif ısı transferi
• Isı transfer katsayısı
• Isı iletkenliği