Епіморфізм — Вікіпедія
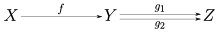
Епіморфізм у категорії ― морфізм , для якого із будь-якої рівності випливає, що (тобто є скорочуваним справа).
У категорії множин роль епіморфізмів відіграють сюр'єкції, у загальній алгебрі ― сюр'єктивні гомоморфізми.
Двоїстим до поняття епіморфізм є поняття мономорфізму. Багато авторів в абстрактній та універсальній алгебрі визначають епіморфізм просто як сюр'єктивний гомоморфізм.
- Добуток двох епіморфізмів є епіморфізмом. Якщо добутком двох морфізмів f*g є епіморфізм, то f має бути епіморфізмом.
- Кожний правий дільник епіморфізму є епіморфізмом.
- Клас усіх об'єктів і клас усіх епіморфізмів довільної категорії утворюють підкатегорію.
Кожен морфізм у конкретній категорії, якому відповідає сюр'єктивна функція є епіморфізмом. Наприклад, сюр'єктивний гомоморфізм груп або графів. У багатьох категоріях протилежне теж правильно. Наприклад, це правильно в категоріях множин, груп, абелевих груп, векторних просторів, правих модулів і топологічних просторів. Однак, наприклад, у категорії кілець вкладення — несюр'єктивний епіморфізм (і, крім того, біморфізм, який не є ізоморфізмом).
Серед інших концепцій вирізняють регулярні епіморфізми, екстремальні епіморфізми, сильні епіморфізми та розділені епіморфізми. Регулярний епіморфізм - епіморфізм, який вирівнює паралельну пару морфізмів. Екстремальний епімрофізм - епіморфізм, який не має мономорфізму за другий фактор, якщо тільки цей мономорфізм не є ізоморфізмом. Розділений епіморфізм - епіморфізм, що має правосторонню інверсію
Морфізм, що є мономорфізмом та епіморфізмом одночасно, називають біоморфізмом. Кожен ізоморфізм є біоморфізмом, проте зворотне не завжди вірно
Парні терміни епіморфізм та мономорфізм були вперше представлені групою вчених Бурбакі. Вони використовували епіморфізм як скорочення до Сюр'єкції. Деякі теоретики вважали, що епіморфізм є правильним аналогом сюр'єкції в довільній категорії, подібно до того, як мономорфізми є майже точною копією ін'єкцій. На жаль, це не є вірним, оскільки регулярні та сильні епіморфізми поводяться набагато більш схоже до сюр'єкцій ніж звичайні епіморфізми. Сандерс Маклейн намагався створити відмінність між епіморфізмами та епічними морфізмами, які і є епіморфізмами у сучасному розумінні. Проте це розходження не прижилося.
Розповсюдженою помилкою є те, що епіморфізми вважають ідентичними покращеними версіями сюр'єкцій. На жаль, це рідко є правдою, оскільки епіморфізми можуть поводити себе дуже несподівано. Наприклад, дуже важко класифікувати всі епіморфізми кілець. Загалом, епіморфізми мають свою унікальну концепцію, схожу до сюр'єкцій, проте в той самий час принципово іншу.
- (укр.) Гаврилків В. М. Елементи теорії груп та теорії кілець. — І.-Ф. : Голіней, 2023. — 153 с.
- С. Мак Лейн Категории для работающего математика. — Физматлит, 2004 [1998].


 French
French Deutsch
Deutsch



