Полярний момент інерції — Вікіпедія

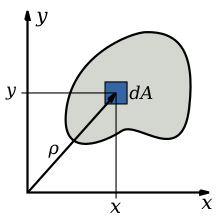
Поля́рний моме́нт іне́рції — геометрична характеристика плоскої фігури, що визначається як сума (інтеграл) добутків площ елементарних площинок dA на квадрат відстані їх від полюса — ρ² (у полярній системі координат), взята по всій площі перерізу. Тобто:

${\displaystyle J_{0}=\iint _{A}\rho ^{2}dA.}$

Ця величина використовується для прогнозування здатності об'єкта чинити опір крученню. Вона має розмірність четвертого степеня одиниці довжини (м⁴, см⁴) і може бути лише додатною.

Для площі перерізу, що має форму кола радіусом r:

${\displaystyle J_{0}=\int _{0}^{2\pi }\int _{0}^{r}\rho ^{2}\rho \,d\rho \,d\phi ={\frac {\pi r^{4}}{2}}}$

Зрозуміло: якщо сумістити початок декартової прямокутної системи координат із полюсом полярної системи (див. рис.), то

${\displaystyle J_{0}=J_{x}+J_{y}}$ тому що ${\displaystyle \rho ^{2}=x^{2}+y^{2}}$.

Полярний момент інерції застосовується у формулах, які описують залежність між дотичними напруженнями та крутним моментом, що їх викликає дотичне напруження:

${\displaystyle \tau ={\frac {Tr}{J_{0}}}}$

де ${\displaystyle T}$ — крутний момент, ${\displaystyle r}$ — відстань від осі кручення і ${\displaystyle {J_{0}}}$ — полярний момент інерції.

Для круглого суцільного перерізу з одиничною густиною:

${\displaystyle J_{p0}=\iint _{x^{2}+y^{2}\leq R}dA=\int _{0}^{2\pi }\int _{0}^{R}r^{2}rdrd\theta ={\frac {\pi R^{4}}{32}}}$

де R — зовнішній радіус кола.

Для кільцевого перерізу просто з полярного моменту інерції більшого круга вираховуємо полярний момент інерції меншого:

${\displaystyle J_{p0}={\frac {\pi R^{4}}{32}}\left(1-{\frac {r^{4}}{R^{4}}}\right)}$

де

R — зовнішній радіус кільця,

r — внутрішній радіус кільця.

• Моменти інерції плоских перерізів

• Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993 .- 655 с. ISBN 5-11-004083-4
• Мильніков О.В. Опір матеріалів. Конспект лекцій. − Тернопіль: Видавництво ТНТУ, 2010. − 257 с.