Теорема Варіньона (геометрія) — Вікіпедія

У Вікіпедії є статті про інші значення цього терміна: Теорема Варіньона.

Теоре́ма Варіньо́на — чотирикутник, вершини якого збігаються з серединами сторін довільного чотирикутника, є паралелограмом, сторони якого паралельні до діагоналей вихідного чотирикутника.

Теорема доведена французьким математиком П'єром Варіньоном (1654–1722) і опублікована у 1731 році у його лекційному курсі «Елементи математики» (фр. «Elemens de mathematique»)^[1].

Скорочене формулювання:

Середини сторін довільного чотирикутника є вершинами паралелограма.

Паралелограм, утворений серединами сторін, іноді називається варіньонівським, варіньоновим чи паралелограмом Варіньона.

Центр паралелограма Варіньона лежить на середині відрізка, що з'єднує середини сторін вихідного чотирикутника (у цій же точці перетинаються відрізки, що з'єднують середини протилежних сторін — діагоналі варіньонівського паралелограма).

Площа паралелограма Варіньона дорівнює половині площі вихідного чотирикутника.

Наслідок з теореми: для прямокутника і рівнобедреної трапеції паралелограмом Варіньона є ромб, а для ромба — прямокутник.

Доведення

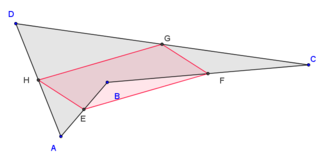
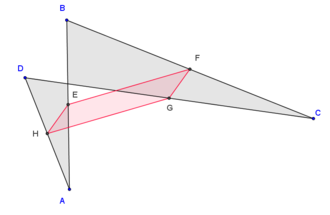
Проведемо діагональ AC. Відрізки EF та GH будуть середніми лініями трикутників $\triangle ABC$ і $\triangle ADC$ . За теоремою про середню лінію, відрізки будуть паралельними до діагоналі, а, значить, і один до одного. Повторивши аналогічні міркування для діагоналі BD, отримуємо, що протилежні сторони чотирикутника EFGH взаємопаралельні, і, за ознаками, це — паралелограм.

Нехай діагональ $AC$ проходить всередині чотирикутника. Тоді площа трикутника $ABC$ дорівнює ${\frac {AC\cdot h_{b}}{2}}$ , де $h_{b}$ --- висота трикутника $ABC$ , що опущена з вершини $B$ . Аналогічно, площа трикутника $ADC$ дорівнює ${\frac {AC\cdot h_{d}}{2}}$ . Тоді площа всього чотрикутника дорівнює ${\frac {AC(h_{b}+h_{d})}{2}}$ . Але ${\frac {(h_{b}+h_{d})}{2}}={\frac {h_{b}}{2}}+{\frac {h_{d}}{2}}$ — це сума відстаней до прямої $AC$ від точок $E$ та $H$ , тобто є висотою паралелограма $EHGF$ . Оскільки сторона $GH$ паралелограма є удвічі меншою $AC$ , то і площа паралелограма дорівнює половині площі $ABCD$ .

Теорема Варіньона справедлива для всіх видів чотирикутників^[2]

опуклий чотирикутник	неопуклий чотирикутник	чотирикутник із сторонами, що перетинаються

Примітки

↑ Elements de mathematique de monsieur Varignon [Архівовано 2011-10-18 у Wayback Machine.]. Lille, 1731.
↑ Coxeter H. S. M. and Greitzer S. L. Quadrangle; Varignon's theorem § 3.1 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 52-54, 1967.

Посилання

Varignon Parallelogram in Compendium Geometry.(англ.)
Weisstein, Eric W. Теорема Варіньона від MathWorld. (англ.)

[1] Elements de mathematique de monsieur Varignon [Архівовано 2011-10-18 у Wayback Machine.]. Lille, 1731.

[2] Coxeter H. S. M. and Greitzer S. L. Quadrangle; Varignon's theorem § 3.1 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 52-54, 1967.

[1]

[2]