Теорема Штейнера — Лемуса — Вікіпедія
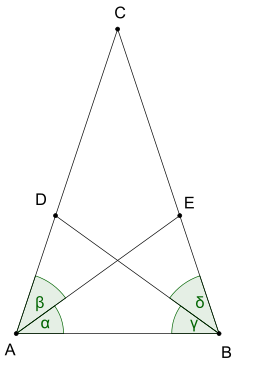
Теорема Штейнера-Лемуса в елементарній геометрії була сформульована Крістіаном Лемусом та згодом доведена Якобом Штейнером.
- Будь-який трикутник з двома рівними бісектрисами є рівнобедреним.
Теорема вперше була сформульована 1840 року в листі К. Лемуса Жаку Штурму, в якому він питав про чисто геометричне доведення. Штурм передав запитання до інших математиків, серед яких одному з перших знайти доведення вдалося Якобу Штейнеру. Теорема стала популярною в елементарній геометрії, відтоді як почалися часті публікації про неї.[1][2][3]
У 1963 році журнал American Mathematical Monthly оголосив конкурс на найкраще доведення теореми. Було надіслано багато доведень, серед яких виявилися цікаві та невідомі раніше. Одне з найкращих, на думку редакції, наведене в книзі Г. С. М. Коксетера та С. П. Грейтцера «Нові зустрічі з геометрією [Архівовано 2 травня 2016 у Wayback Machine.]» та використовує метод від супротивного, надалі розглядаючи одне коло чотирьох точок.
У радянській літературі поширене доведення, засноване на такій ознаці рівності трикутників: якщо сторона, протилежний їй кут та бісектриса цього кута одного трикутника дорівнюють відповідним елементам іншого трикутника, то такі трикутники рівні.
- ↑ Coxeter, H. S. M. and Greitzer, S. L. "The Steiner–Lehmus Theorem." §1.5 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 14–16, 1967.
- ↑ Diane and Roy Dowling: The Lasting Legacy of Ludolph Lehmus [Архівовано 4 березня 2016 у Wayback Machine.]. Manitoba Math Links – Volume II – Issue 3, Spring 2002
- ↑ Barbara, Roy, "Steiner–Lehmus, revisited", Mathematical Gazette 91, November 2007, 528–529.


 French
French Deutsch
Deutsch
