五引理 - 维基百科,自由的百科全书
在同調代數中,五引理是關於交換圖的一個重要引理。五引理可以被視為兩個相對偶的四引理之組合。此結果不只對阿貝爾範疇成立,也對群範疇成立。
陳述
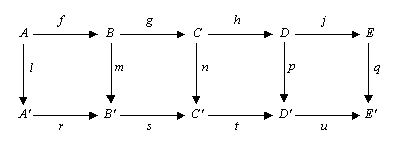
[编辑]在任一阿貝爾範疇(例如阿貝爾群或模的範疇)或群範疇中,考慮以下的交換圖:
五引理的敘述是:如果橫列正合, 是同構, 是滿射而 是單射,則 是同構。
兩個四引理的敘述是:
若其橫行正合, 是滿射而 是單射,則 是滿射。
若其橫行正合, 是單射而 是滿射,則 是單射。
證明
[编辑]以下採用的證法俗稱「圖追蹤」,它看似繁複,其實習慣後只是例行程序罷了。
為進行圖追蹤,以下假設所論範疇為某個環上的模範疇,因此可以談論對象的元素,並將態射視為模的同態。此時單射、滿射等等性質相應於集合論意義上的性質。根據Mitchell嵌入定理,可導出一般範疇上的情形。
對於群範疇,僅須注意到證明內容未用到群的交換性。
- 設 。
- 由於 是滿射,存在 使得 。
- 根據圖的交換性,。
- 根據正合性, ,故 。
- 因為 是單射,,故 。
- 於是存在 使得 。
- 遂有 。因為 是同態,有 。
- 根據正合性,,故存在 使得 。
- 因為 是滿射,存在 使得 。
- 根據圖的交換性 。
- 因為 是同態,。
- 由此可知 是滿射。證畢。
為證明 (2),在下圖中假設 與 是單射,而 是滿射。
- 設 使得 。
- 於是 。
- 根據圖的交換性,
- 因為 是單射,。
- 根據正合性,存在 使得 。
- 根據圖的交換性,。
- 根據正合性,存在 使得 。
- 因為 是滿射,存在 使得 。
- 根據圖的交換性,。
- 因為 是單射,。
- 故 。
- 由此可知 是單射。證畢。
結合兩個四引理,便可證得五引理。
應用
[编辑]五引理通常用於長正合序列:在計算一個對象的同調或上同調群時,我們通常利用一個較簡單的子對象,其同調或上同調已知,再配合長正合序列進行計算。長正合序列本身不一定能確定所求的同調或上同調,此時可以試著以態射比較原對象與一個已知的對象,此態射導出長正合序列的鏈映射,此時五引理有助於決定未知的同調或上同調群。


 French
French Deutsch
Deutsch