洛伦兹力 - 维基百科，自由的百科全书

本条目中，向量與标量分別用粗體與斜體顯示。例如，位置向量通常用 ${\displaystyle \mathbf {r} \,\!}$ 表示；而其大小則用 ${\displaystyle r\,\!}$ 來表示。

在電動力學裡，勞侖茲力（Lorentz force）是運動於電磁場的帶電粒子所感受到的作用力。勞侖茲力是因荷蘭物理學者亨德里克·勞侖茲而命名。根據勞侖茲力定律，勞侖茲力可以用方程式，稱為勞侖茲力方程式，表達為

${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$；

其中，${\displaystyle \mathbf {F} }$是勞侖茲力，${\displaystyle q}$是帶電粒子的電荷量，${\displaystyle \mathbf {E} }$是電場强度，${\displaystyle \mathbf {v} }$是帶電粒子的速度，${\displaystyle \mathbf {B} }$是磁感应强度。

勞侖茲力定律是一個基本公理，不是從別的理論推導出來的定律，而是由多次重複完成的實驗所得到的同樣的結果。

感受到電場的作用，正電荷會朝著電場的方向加速；但是感受到磁場的作用，按照右手定則，正電荷會朝著垂直於速度${\displaystyle \mathbf {v} }$和磁場${\displaystyle \mathbf {B} }$的方向彎曲（詳細地說，假設右手的大拇指與${\displaystyle \mathbf {v} }$同向，食指與${\displaystyle \mathbf {B} }$同向，則掌心推出的方向为${\displaystyle \mathbf {F} }$的方向）。

勞侖茲力方程式的${\displaystyle q\mathbf {E} }$項目是電場力項目，${\displaystyle q\mathbf {v} \times \mathbf {B} }$項目是磁場力項目^[1]。處於磁場內的載電導線感受到的磁場力就是這勞侖茲力的磁場力分量。

勞侖茲力方程式的积分形式为

${\displaystyle \mathbf {F} =\int _{\mathbb {V} }(\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} )\ \mathrm {d} \tau }$。

其中，${\displaystyle \mathbb {V} }$是積分的體積，${\displaystyle \rho }$是電荷密度，${\displaystyle \mathbf {J} }$是電流密度，${\displaystyle \mathrm {d} \tau }$是微小體元素。

勞侖茲力密度${\displaystyle \mathbf {f} }$是單位體積的勞侖茲力，表達為：

${\displaystyle \mathbf {f} =\rho \mathbf {E} +\rho \mathbf {v} \times \mathbf {B} =\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} }$。

1892年，荷兰物理学家亨德里克·勞侖茲提出勞侖茲力的概念^[2]。但是，在勞侖茲之前，就已經有發掘出勞侖茲力方程式的形式，特別是在詹姆斯·馬克士威的1861年論文《論物理力線》裏的公式（77）：

${\displaystyle P=\mu \gamma {\frac {dy}{dt}}-\mu \beta {\frac {dz}{dt}}+{\frac {dF}{dt}}-{\frac {d\Psi }{dx}}}$、

${\displaystyle Q=\mu \alpha {\frac {dz}{dt}}-\mu \gamma {\frac {dx}{dt}}+{\frac {dG}{dt}}-{\frac {d\Psi }{dy}}}$、

${\displaystyle R=\mu \beta {\frac {dx}{dt}}-\mu \alpha {\frac {dy}{dt}}+{\frac {dH}{dt}}-{\frac {d\Psi }{dz}}}$；

其中，${\displaystyle P}$、${\displaystyle Q}$、${\displaystyle R}$分別為電場的三個分量，${\displaystyle \mu }$是磁導率，${\displaystyle {\frac {dx}{dt}}}$、${\displaystyle {\frac {dy}{dt}}}$、${\displaystyle {\frac {dz}{dt}}}$分別為導電體的移動速度的三個分量，${\displaystyle \alpha }$、${\displaystyle \beta }$、${\displaystyle \gamma }$分別為磁場強度的三個分量，${\displaystyle F}$、${\displaystyle G}$、${\displaystyle H}$分別為磁矢勢的三個分量，${\displaystyle \Psi }$是電勢。

後來，在他的1864年論文《電磁場的動力學理論》裏，馬克士威將這公式列為馬克士威方程組的八個原本方程式中的方程式（D）:

${\displaystyle \mathbf {E} =\mathbf {v} \times (\mu \mathbf {H} )-{\frac {\partial \mathbf {A} }{\partial t}}-\nabla \phi }$；

其中，${\displaystyle \mathbf {v} }$是速度，${\displaystyle \mathbf {H} }$是磁場強度，${\displaystyle \mu }$是磁導率，${\displaystyle \mathbf {A} }$是磁矢勢，${\displaystyle \phi }$是電勢。

很明顯地，馬克士威版是現代版的前導。兩個版本的差別為：

• 馬克士威版並沒有特意地提到電荷。馬克士威稱物理量${\displaystyle \mathbf {E} }$為電動力（electromotive force）。這英文原文與電動勢的英文原文相同。很多物理學家都對英文原文表示意見，認為會造成困惑，是個相當不精確的術語。從方程式形式和單位分析方面來看，這物理量對應於現代的物理量單位電荷的勞侖茲力。
• 馬克士威版包含有現在稱為電場的項目，以電勢${\displaystyle \phi }$和磁向量勢${\displaystyle \mathbf {A} }$來表達：

${\displaystyle \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}$。

取旋度於這表達式，就可以得到法拉第-馬克士威方程式^[1]：

${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$。

因此，這表達式等價於法拉第-馬克士威方程式。儘管勞侖茲力方程式來自於原本的一條馬克士威方程式，現在，經過奧利弗·黑維塞重新表述後的勞侖茲力方程式，不再被視為馬克士威方程組中的一員，而成為伴隨馬克士威方程組的一條獨立基要的定律。

當馬克士威方程組描繪帶電粒子怎樣產生電磁場的同時，勞侖茲力方程式描繪了移動於電磁場的帶電粒子所感受到的電磁力。這使得整個電磁動力的圖畫得以完整。在一個複雜的物理系統裏，帶電粒子可能還會感受到別種作用力，像萬有引力或核力。馬克士威方程組並非與這些作用力完全無關；而是通過帶電粒子或電流密度與這些作用力耦合。

對於實際的物質，在原則上和計算的複雜程度上，勞侖茲力方程式都不足以描述一群粒子的物理行為。在物質介質裏的帶電粒子，必須同時地響應和生成電磁場。除此以外，還必須考慮到描述這一群粒子的運動的傳輸方程式，例如，波茲曼傳輸方程式（Boltzmann equation）、福克-普朗克方程式^[3]（Fokker–Planck equation）、納維-斯托克斯方程式、等等。請參閱磁流體力學、超導現象、恆星演化、等等。在這些學術領域研究的科學家必須解析複雜的傳輸方程式，求得帶電粒子在時間和空間方面的響應。

或許有些讀者會認為這些理論只是靠著近似來處理一個大系綜的帶電粒子。從更深的層面來看，帶電粒子也會對非電磁力，像萬有引力，核力或邊界條件等等，產生響應。

給予作用於粒子的勞侖茲力的公式，將這公式代入牛頓第二運動定律，可以得到粒子的運動方程式。解析這運動方程式，就可以找到粒子的運動軌道。

在一個簡單的迴旋加速器內，均勻磁場是${\displaystyle \mathbf {B} =B_{0}{\hat {\mathbf {z} }}}$，電場是零。那麼，運動於xy-平面的帶電粒子${\displaystyle q}$所感受到的勞侖茲力${\displaystyle \mathbf {F} }$為

${\displaystyle \mathbf {F} =q\mathbf {v} \times \mathbf {B} }$。

將這公式代入牛頓第二運動定律，

${\displaystyle m\mathbf {a} =q\mathbf {v} \times \mathbf {B} }$；

其中，${\displaystyle m}$是帶電粒子的質量，${\displaystyle \mathbf {a} }$是帶電粒子的加速度。

由於帶電粒子的加速度與速度互相垂直，帶電粒子呈圓周運動。假設粒子帶有正電荷，則這公式的一般解答為

${\displaystyle \mathbf {r} =r_{c}(\cos \omega t,\,-\sin \omega t,\,0)}$；

其中，${\displaystyle \mathbf {r} }$是帶電粒子的圓周運動軌道，${\displaystyle r_{c}}$是圓周半徑，${\displaystyle \omega =qB/m}$是旋轉角速度，${\displaystyle t}$是時間。

朝著均勻磁場方向看，帶電粒子會以反時針方向，呈等速圓周運動。給予初始速率${\displaystyle v_{0}}$。那麼，圓周半徑為

${\displaystyle r_{c}=v_{0}/\omega =mv_{0}/qB}$。

這圓周半徑稱為迴旋半徑（cyclotron radius）或拉莫半徑（Larmor radius）。${\displaystyle \omega =qB/m}$稱為迴旋頻率（cyclotron frequency）。

帶電粒子的動量${\displaystyle p_{0}}$為

${\displaystyle p_{0}=mv_{0}=qBr_{c}}$。

假設粒子帶有負電荷，則運動方向會逆反，改為順時針方向。

假設初始速度有一個z-分量${\displaystyle v_{z0}}$，則帶電粒子會呈等速螺旋運動。

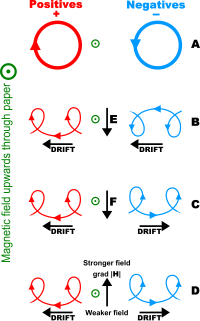
對於很多有意思的、比較複雜的實際案例，在磁場內運動的帶電粒子（例如，電漿的電子或離子），可以分為兩部分處理。這兩部分的疊加，足以描述這帶電粒子的物理行為。第一部分是速度比較快的，環繞著某一點的圓周運動。環繞之點稱為導向中心（guiding center）。另一部分是導向中心的漂移運動。其速度比較慢，會因不同種類的粒子而不同，又跟其電荷量、質量或溫度有關。不同的漂移速度可能會造成電流或化學分離。

許多經典電磁學教科書會用勞侖茲力定律來定義電場和磁場。

假設檢驗電荷靜止不動，${\displaystyle \mathbf {v} =0}$，則勞侖茲力方程式變為

${\displaystyle \mathbf {F} =q\mathbf {E} }$。

採用國際單位制，假設檢驗電荷的電量為1庫侖，作用於檢驗電荷的勞倫茲力為1牛頓，則檢驗電荷感受到的電場為1牛頓／庫侖。

假設電場為零，則作用於電荷${\displaystyle q}$的勞侖茲力是

${\displaystyle \mathbf {F} =q\mathbf {v} \times \mathbf {B} }$。

對於一條線電荷密度為${\displaystyle \lambda }$的載流導線，總作用力為

${\displaystyle \mathbf {F} =\int _{\mathbb {C} }\mathbf {v} \times \mathbf {B} \mathrm {d} q=\int _{\mathbb {C} }\mathbf {v} \times \mathbf {B} \lambda \mathrm {d} \ell =\int _{\mathbb {C} }\mathbf {I} \times \mathbf {B} \mathrm {d} \ell }$；

其中，${\displaystyle \mathbb {C} }$是積分路徑，${\displaystyle \mathbf {I} =\lambda \mathbf {v} }$是電流向量。

假設電流是穩定電流，則可以將電流從積分內提出，用向量${\displaystyle \mathrm {d} {\boldsymbol {\ell }}}$來表示電流${\displaystyle \mathbf {I} }$的方向：

${\displaystyle \mathbf {F} =I\int _{\mathbb {C} }\mathrm {d} {\boldsymbol {\ell }}\times \mathbf {B} }$。

這公式給出了，在磁場內，載流導線感受到的磁場力。

使用這公式和必歐-沙伐定律，就可以推導出安培力定律（詳盡細節，請參閱安培力定律）。

假設，磁場是均勻磁場，積分路徑是垂直於磁場的直線，則

${\displaystyle F=ILB}$；

其中，${\displaystyle L}$是積分路徑${\displaystyle \mathbb {C} }$的長度，

採用國際單位制，假設檢驗電流為1安培，作用於載流導線的單位長度的勞侖茲力為1牛頓/公尺，則檢驗電流感受到的磁場為1特斯拉。

許多發電機的基本運作原理涉及動生電動勢概念。將導線移動於磁場，則會產生電動勢，稱為動生電動勢。如圖右^[4]，假設一條長度為${\displaystyle L}$的細直導線，以速度${\displaystyle \mathbf {v} }$移動於磁場${\displaystyle \mathbf {B} }$。磁場${\displaystyle \mathbf {B} }$以箭尾或叉叉表示，方向由銀幕外部指入銀幕。思考在這導線內的電荷${\displaystyle q}$，根據勞侖茲定律，會感受到勞侖茲力${\displaystyle \mathbf {F} _{lorentz}}$：

${\displaystyle \mathbf {F} _{lorentz}=q\mathbf {v} \times \mathbf {B} }$。

在這裡，勞侖茲力也是磁場力。因為這磁場力的作用，正電荷會往導線的上端移動，負電荷會往導線的下端移動。在穩定平衡狀態，這會感應出一個電場${\displaystyle \mathbf {E} }$：

${\displaystyle \mathbf {E} =-\mathbf {v} \times \mathbf {B} }$。

電動勢定義為造成開路電路的兩個終端的電勢差，對於每單位電荷所需做的功。所以，動生電動勢${\displaystyle {\mathcal {E}}}$為

${\displaystyle {\mathcal {E}}=\int _{L}{\frac {\mathbf {F_{lorentz}} }{q}}\cdot d{\boldsymbol {\ell }}=vBL}$。

在這個例子裏，穩定平衡狀態時的電流等於零。假設載流導線與其他原件連結成一個電路，則會因為動生電動勢而產生電流。例如，將一個電阻${\displaystyle R}$與導線的兩端相連結，則流過電阻的電流${\displaystyle I}$為

${\displaystyle I={\mathcal {E}}/R=vBL/R}$。

法拉第電磁感應定律闡明，穿過任意閉迴路的磁通量的變化率，與這迴路的電動勢成正比：

${\displaystyle {\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}}$；

其中，${\displaystyle {\mathcal {E}}}$是電動勢，${\displaystyle \Phi _{B}}$是磁通量，${\displaystyle t}$是時間。

在時間${\displaystyle t}$通過任意曲面${\displaystyle \Sigma (t)}$的磁通量${\displaystyle \Phi _{B}(t)}$定義為

${\displaystyle \Phi _{B}(t)\ {\stackrel {def}{=}}\ \int _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} }$；

其中，${\displaystyle \mathbf {r} }$是位置，${\displaystyle d\mathbf {a} }$是微小面元素。

給予一個以常速度${\displaystyle \mathbf {v} }$移動於磁場的閉迴路${\displaystyle \partial \Sigma (t)}$。那麼，磁通量對於時間的全微分是^[5]

${\displaystyle {\begin{aligned}d\Phi _{B}(t)&=\int _{\Sigma (t+dt)}\mathbf {B} (\mathbf {r} ,\,t+dt)\cdot d\mathbf {a} -\int _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} \\&=\int _{\Sigma (t+dt)}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} +\int _{\Sigma (t+dt)}{\frac {\partial \mathbf {B} (\mathbf {r} ,\,t)}{\partial t}}dt\cdot d\mathbf {a} -\int _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} \\&=\int _{\Sigma (t+dt)}{\frac {\partial \mathbf {B} (\mathbf {r} ,\,t)}{\partial t}}dt\cdot d\mathbf {a} +\int _{\Sigma _{total}}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} -\int _{\Sigma _{ribbon}}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} \\\end{aligned}}}$ ；

其中，${\displaystyle \Sigma (t)}$是邊緣為${\displaystyle \partial \Sigma (t)}$的曲面，${\displaystyle \Sigma _{total}}$是包括${\displaystyle \Sigma (t+dt)}$、${\displaystyle -\Sigma (t)}$和${\displaystyle \Sigma _{ribbon}}$的閉曲面，${\displaystyle \Sigma _{ribbon}}$是邊緣${\displaystyle \partial \Sigma (t+dt)}$和${\displaystyle \partial \Sigma (t)}$形成的邊緣曲面。

根據散度定理和高斯磁定律，

${\displaystyle \int _{\Sigma _{total}}\mathbf {B} \cdot d\mathbf {a} =\int _{\mathbb {V} _{total}}\nabla \cdot \mathbf {B} d\tau =0}$；

其中，${\displaystyle \mathbb {V} _{total}}$是閉曲面${\displaystyle \Sigma _{total}}$包含的空間，${\displaystyle d\tau }$是微小體元素。

通過邊緣曲面${\displaystyle \Sigma _{ribbon}}$的磁通量可以改變成一個線積分：

${\displaystyle \int _{\Sigma _{ribbon}}\mathbf {B} \cdot d\mathbf {a} =\int _{\partial \Sigma (t)}\mathbf {B} \cdot [d{\boldsymbol {\ell }}\times (\mathbf {v} dt)]=\int _{\partial \Sigma (t)}[(\mathbf {v} dt)\times \mathbf {B} ]\cdot d{\boldsymbol {\ell }}}$。

所以，磁通量對於時間的全導數，或磁通量的變化率為

${\displaystyle {\frac {d\Phi _{B}(t)}{dt}}=\int _{\Sigma (t+dt)}{\frac {\partial \mathbf {B} (\mathbf {r} ,\,t)}{\partial t}}\cdot d\mathbf {a} -\int _{\partial \Sigma (t)}\mathbf {v} \times \mathbf {B} \cdot d{\boldsymbol {\ell }}}$。

運動於移動的閉迴路${\displaystyle \partial \Sigma (t)}$的一個電荷${\displaystyle q}$的速度${\displaystyle \mathbf {w} }$為

${\displaystyle \mathbf {w} =\mathbf {u} +\mathbf {v} }$；

其中，${\displaystyle \mathbf {u} }$是相對於閉迴路${\displaystyle \partial \Sigma (t)}$的電荷運動速度，${\displaystyle \mathbf {v} }$是閉迴路${\displaystyle \partial \Sigma (t)}$的移動速度。

這電荷會感受到勞侖茲力

${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {w} \times \mathbf {B} )}$；

電動勢${\displaystyle {\mathcal {E}}}$定義為

${\displaystyle {\mathcal {E}}\ {\stackrel {def}{=}}\ \int _{\partial \Sigma }{\frac {\mathbf {F} }{q}}\cdot d{\boldsymbol {\ell }}=\int _{\partial \Sigma }(\mathbf {E} +\mathbf {w} \times \mathbf {B} )\cdot d{\boldsymbol {\ell }}}$。

根據法拉第電磁感應定律，

${\displaystyle {\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}=\int _{\partial \Sigma }(\mathbf {E} +\mathbf {w} \times \mathbf {B} )\cdot d{\boldsymbol {\ell }}}$。

在計算積分時，閉迴路${\displaystyle \partial \Sigma (t)}$的微小線元素${\displaystyle d{\boldsymbol {\ell }}}$與正在那位置的電荷的${\displaystyle \mathbf {u} }$平行。所以，

${\displaystyle {\frac {d\Phi _{B}(t)}{dt}}=-\int _{\partial \Sigma }(\mathbf {E} +\mathbf {v} \times \mathbf {B} )\cdot d{\boldsymbol {\ell }}}$。

令兩個磁通量變化率的方程式相等，除去同有的移動的閉迴路項目，則可得到

${\displaystyle \int _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\int _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}\cdot d\mathbf {a} }$。

應用斯托克斯定理，${\displaystyle \int _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=\int _{\Sigma }\nabla \times \mathbf {E} \cdot d\mathbf {a} }$，可以得到

${\displaystyle \int _{\Sigma }\left(\nabla \times \mathbf {E} +{\frac {\partial \mathbf {B} }{\partial t}}\right)\cdot d\mathbf {a} =0}$。

由於${\displaystyle \Sigma }$是任意取面，可以將被積式從積分中取出：

${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$。

這是馬克士威-法拉第方程式。由於這方程式的右手邊是個對於時間的偏導數項目，只涉及固定的閉迴路，不能用來計算移動中的閉迴路。

用馬克士威-法拉第方程式，通常對於時間的偏導數的詮釋只限制為固定邊界。而在另一方面，不論導線的閉迴路是剛硬固定的、是在運動中、是在形變過程中，不論磁場是不含時的或含時的，法拉第電磁感應定律都成立。但是，對於某些案例，法拉第電磁感應定律並不適用或使用起來很困難。這時候，必須使用勞侖茲力定律。詳盡細節，請參閱法拉第電磁感應定律不適用案例。

假設閉迴路移動於不含時間的磁場${\displaystyle \mathbf {B} }$，通過閉迴路的磁通量${\displaystyle \Phi _{B}}$會因為幾種因素而改變：例如，假若磁場${\displaystyle \mathbf {B} }$隨著位置改變，閉迴路移動至不同磁場${\displaystyle \mathbf {B} }$的位置，則磁通量${\displaystyle \Phi _{B}}$會改變。或者，假若相對於磁場，閉迴路的定向改變，由於微小元素${\displaystyle \mathbf {B} \cdot d\mathbf {A} }$的改變，磁通量${\displaystyle \Phi _{B}}$也會改變。再舉一個例子，假若閉迴路掃掠過一個均勻的不含時磁場，由於閉迴路的形變，磁通量${\displaystyle \Phi _{B}}$會改變。對於這三個案例，法拉第電磁感應定律正確地計算出磁通量變化率${\displaystyle {\frac {d\Phi _{B}}{dt}}}$所產生的電動勢。

對比前面所述狀況，假設固定的閉迴路處於含時磁場${\displaystyle \mathbf {B} }$，馬克士威-法拉第方程式會顯示出一個非保守性的電場${\displaystyle \mathbf {E} }$產生於閉迴路，靠著勞侖茲力的${\displaystyle q\mathbf {E} }$項目，驅使載電粒子移動於導線。這狀況也會改變磁通量${\displaystyle \Phi _{B}}$，法拉第電磁感應定律也會正確地計算出磁通量變化率${\displaystyle {\frac {d\Phi _{B}}{dt}}}$所產生的電動勢。

根據亥姆霍兹分解（Helmholtz decomposition），電場和磁場可以用電勢${\displaystyle \phi }$和磁向量勢${\displaystyle \mathbf {A} }$來表達：

${\displaystyle \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}$

${\displaystyle \mathbf {B} =\nabla \times \mathbf {A} }$

其中∇为梯度，∇⋅ 为散度，∇× 为旋度。

將這兩個公式代入勞侖茲力方程式，則可得到

${\displaystyle \mathbf {F} =q\left[-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\mathbf {v} \times (\nabla \times \mathbf {A} )\right]}$

可以化简为

定義粒子的四維速度${\displaystyle u_{\beta }}$為

${\displaystyle u_{\beta }\ {\stackrel {def}{=}}\ (u_{0},\,u_{1},\,u_{2},\,u_{3})=\gamma (c,\,-v_{x},\,-v_{y},\,-v_{z})}$；

其中，${\displaystyle \gamma }$是勞侖茲因子，${\displaystyle c}$是光速，${\displaystyle \mathbf {v} =(v_{x},\,v_{y},\,v_{z})}$是粒子的速度向量。

定義電磁場張量${\displaystyle F^{\alpha \beta }}$為

${\displaystyle F^{\alpha \beta }\ {\stackrel {def}{=}}\ {\begin{bmatrix}0&-E_{x}/c&-E_{y}/c&-E_{z}/c\\E_{x}/c&0&-B_{z}&B_{y}\\E_{y}/c&B_{z}&0&-B_{x}\\E_{z}/c&-B_{y}&B_{x}&0\end{bmatrix}}}$；

其中，${\displaystyle \mathbf {E} }$是電場向量，${\displaystyle \mathbf {B} }$是磁場向量。

結合牛頓運動定律與勞侖茲力定律在一起，以電磁場張量寫為反變形式（contravariant form）：

${\displaystyle {\frac {dp^{\alpha }}{d\tau }}=qu_{\beta }F^{\alpha \beta }}$；

其中，${\displaystyle p^{\alpha }}$是四維動量，${\displaystyle \tau }$是粒子的固有時。

應用勞侖茲變換，電磁場張量可以從一個參考系${\displaystyle S}$轉換到另一個參考系${\displaystyle {\bar {S}}}$：

${\displaystyle {\bar {F}}^{\mu \nu }={\Lambda ^{\mu }}_{\alpha }{\Lambda ^{\nu }}_{\beta }F^{\alpha \beta }}$；

其中，${\displaystyle {\Lambda ^{\mu }}_{\alpha }}$和${\displaystyle {\Lambda ^{\nu }}_{\beta }}$是勞侖茲變換矩陣。

換另一種方法，定義四維勢${\displaystyle A^{\alpha }}$為

${\displaystyle A^{\alpha }\ {\stackrel {def}{=}}\ (\phi /c,\,A_{x},\,A_{y},\,A_{z})}$；

其中，${\displaystyle \phi }$是電勢，${\displaystyle \mathbf {A} }$是磁向量勢。

定義四維坐標 ${\displaystyle x_{\alpha }}$為

${\displaystyle x_{\alpha }\ {\stackrel {def}{=}}\ (ct,\,-x,\,-y,\,-z)}$。

那麼，電磁場張量為^[1]

${\displaystyle F^{\alpha \beta }={\frac {\partial A^{\beta }}{\partial x_{\alpha }}}-{\frac {\partial A^{\alpha }}{\partial x_{\beta }}}}$。

先計算四維力（four-force）的${\displaystyle \mu =1}$分量（x-分量）：

${\displaystyle \gamma {\frac {dp^{1}}{dt}}={\frac {dp^{1}}{d\tau }}=qu_{\beta }F^{1\beta }=q\left(u_{0}F^{10}+u_{1}F^{11}+u_{2}F^{12}+u_{3}F^{13}\right)}$。

將電磁場張量的分量代入，可以得到

${\displaystyle \gamma {\frac {dp^{1}}{dt}}=q\left(u_{0}\left({\frac {E_{x}}{c}}\right)+u_{2}(-B_{z})+u_{3}(B_{y})\right)}$。

再將四維速度的分量代入，則會得到

${\displaystyle \gamma {\frac {dp^{1}}{dt}}=q\gamma \left(c\left({\frac {E_{x}}{c}}\right)+v_{y}B_{z}-v_{z}B_{y}\right)=q\gamma [E_{x}+(\mathbf {v} \times \mathbf {B} )_{x}]}$。

類似地，可以計算出四維力的${\displaystyle \mu =2}$和${\displaystyle \mu =3}$分量。所以，

${\displaystyle {\frac {d\mathbf {p} }{dt}}=q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$。

• National High Magnetic Field Laboratory的Java互動教學網頁：勞侖茲力。