一个半径 为 r 的圆的面积 [ 1] π r 2 {\displaystyle \pi r^{2}} 希腊字母 π ,和通常一样代表圆周 长和直径 的比值,即為圆周率 。
现代数学家 可以用微积分 或更高深的后继理论实分析 得到这个面积。但是,在古希腊 ,数学家阿基米德 在《圆的测量 欧几里得几何 证明了一个圆周内部的面积等於一個以其圓周長及半徑作為兩個直角邊 的直角三角形 面積。周长为 2 π r {\displaystyle 2\pi r} π r 2 {\displaystyle \pi r^{2}} 中國 古代流傳之《九章算術 ·方田》章中的圓田術對圓面積計算的敘述為“半周半徑相乘得積步”。魏晉 時代的劉徽 注解《九章算術》時,則以“窮盡”割圓術提供了相同結果的證明。
除了这上述古老和现代的方法,我们也考察一些具有历史和实际兴趣的不同方法。
按照阿基米德(Archimedes & 260 BCE )的方法,比较一个圆与底为圆周长高为半径的直角三角形。如果圆与三角形的面积不相等,那么必为大于或小于。我们用反证法 排除这两种情形,剩下惟一可能就是等于。证明的关键是利用正多边形 。
正方形和正八边形内接于圆,显示了面积差 假设圆面积 C {\displaystyle C} T = 1 2 c r {\displaystyle T={\frac {1}{2}}cr} E {\displaystyle E} 弓形 。如果这四个弓形的总面积 G 4 {\displaystyle G_{4}} E {\displaystyle E} G 8 {\displaystyle G_{8}} G n {\displaystyle G_{n}} E {\displaystyle E} P n = C − G n {\displaystyle P_{n}=C-G_{n}}
E = C − T > G n P n = C − G n > C − E P n > T {\displaystyle {\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}} 但这产生了矛盾:从圆心向正多边形的每一边作垂线 ,垂线的长度 h {\displaystyle h} s {\displaystyle s} n s {\displaystyle ns} n {\displaystyle n} s {\displaystyle s} h {\displaystyle h} 1 2 n h s {\displaystyle {\frac {1}{2}}nhs} h < r {\displaystyle h<r} n s < c {\displaystyle ns<c} 1 2 c r {\displaystyle {\frac {1}{2}}cr} C {\displaystyle C} T {\displaystyle T}
圆外切正方形和正八边形,显示了面积差 假设圆面积小于三角形的面积。记 D {\displaystyle D} G 4 {\displaystyle G_{4}} D {\displaystyle D} D {\displaystyle D} P n {\displaystyle P_{n}} T {\displaystyle T}
D = T − C > G n P n = C + G n < C + D P n < T {\displaystyle {\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}} 这样同样得到了矛盾:因为圆心到多边形各边的垂线是半径,长为 r {\displaystyle r} n 个全等的三角形组成,总面积大于 T {\displaystyle T} C {\displaystyle C} T {\displaystyle T}
所以圆的面积一定恰好和三角形的面积相等。这样便证明了结论。
圆面积重排 按照 Satō Moshun (佐藤茂春《算法天元指南》) (Smith & Mikami 1914 ,pp. 130–132)和列奥纳多·达芬奇 (Beckmann 1976 ,p. 19)的方法,我们可用另一方式使用圆内接正多边形。假设我们有一个内接正六边形 。将其从圆心剪开为 6 个三角形。相对的两个三角形和两条相同的直径相接;沿着一条滑动,这样辐射状的边变为相邻。它们现在组成了一个平行四边形 ,六边形的边组成了一组相对底边 s {\displaystyle s} h {\displaystyle h} 2 n {\displaystyle 2n} 2 n s {\displaystyle 2ns} h {\displaystyle h} π r {\displaystyle \pi r} r {\displaystyle r}
重排正 n {\displaystyle n} 边形求单位圆面积 多边形 平行四边形 n {\displaystyle n} 边 底 高 面积 4 1.4142136 2.8284271 0.7071068 2.0000000 6 1.0000000 3.0000000 0.8660254 2.5980762 8 0.7653669 3.0614675 0.9238795 2.8284271 10 0.6180340 3.0901699 0.9510565 2.9389263 12 0.5176381 3.1058285 0.9659258 3.0000000 14 0.4450419 3.1152931 0.9749279 3.0371862 16 0.3901806 3.1214452 0.9807853 3.0614675 96 0.0654382 3.1410320 0.9994646 3.1393502 ∞ {\displaystyle \infty } 1 ∞ {\displaystyle {\frac {1}{\infty }}} π {\displaystyle \pi } 1 π {\displaystyle \pi }
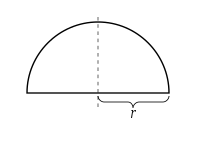
通过环形积分求圆的面积 使用微积分,我们将圆像洋葱一样分为薄圆环,递增地求出面积。这是二维微积分学 。对“洋葱”以 t 为半径的无穷薄圆环,贡献的面积是 2 π t d t {\displaystyle 2\pi t\;dt} r {\displaystyle r}
A r e a ( r ) = ∫ 0 r 2 π t d t = [ ( 2 π ) t 2 2 ] t = 0 r = π r 2 . {\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=\left[(2\pi ){\frac {t^{2}}{2}}\right]_{t=0}^{r}\\&{}=\pi r^{2}.\end{aligned}}} 半径为r 的半圆 利用三角换元法 ,我们代换 x = r sin θ {\displaystyle x=r\sin \theta }
d x = r cos θ d θ {\displaystyle dx=r\cos \theta \,d\theta } θ = arcsin ( x r ) {\displaystyle \theta =\arcsin \left({\frac {x}{r}}\right)} 圆面积 = 2 ∫ − r r r 2 − x 2 d x {\displaystyle =2\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx}
= 4 ∫ 0 r r 2 − x 2 d x {\displaystyle =4\int _{0}^{r}{\sqrt {r^{2}-x^{2}}}\,dx} = 4 ∫ 0 π 2 r 2 ( 1 − sin 2 θ ) ⋅ r cos θ d θ {\displaystyle =4\int _{0}^{\frac {\pi }{2}}{\sqrt {r^{2}(1-\sin ^{2}\theta )}}\cdot r\cos \theta \,d\theta } = 4 r 2 ∫ 0 π 2 cos 2 θ d θ {\displaystyle =4r^{2}\int _{0}^{\frac {\pi }{2}}\cos ^{2}\theta \,d\theta } 利用三角恒等式 cos 2 θ = 2 cos 2 θ − 1 {\displaystyle \cos 2\theta =2\cos ^{2}\theta \ -1}
= 2 r 2 ∫ 0 π 2 ( 1 + cos 2 θ ) d θ {\displaystyle =2r^{2}\int _{0}^{\frac {\pi }{2}}(1+\cos 2\theta )\,d\theta } = 2 r 2 [ θ + 1 2 sin 2 θ ] 0 π 2 {\displaystyle =2r^{2}\left[\theta +{\frac {1}{2}}\sin 2\theta \right]_{0}^{\frac {\pi }{2}}} = π r 2 . {\displaystyle =\pi r^{2}.} 阿基米德算法逼近圆的面积数值非常费力,他算到96边形就停下了。日後出現一个更快的方法,由威理博·斯涅尔 提出(Cyclometricus ,1962年 [來源請求] 惠更斯 步其后尘(De Circuli Magnitudine Inventa ,1654年), Gerretsen & Verdenduin (1983 ,pp. 243–250) 记载这种方法。
给定一个圆周,设 u n {\displaystyle u_{n}} n {\displaystyle n} U n {\displaystyle U_{n}} n {\displaystyle n}
u 2 n = U 2 n u n {\displaystyle u_{2n}={\sqrt {U_{2n}u_{n}}}} 几何平均 ) U 2 n = 2 U n u n U n + u n {\displaystyle U_{2n}={\frac {2U_{n}u_{n}}{U_{n}+u_{n}}}} 调和平均 )阿基米德将一个六边形翻倍4次得到了96边形。对一个单位圆,一个内接正六边形有 u 6 = 6 {\displaystyle u_{6}=6} U 6 = 4 3 {\displaystyle U_{6}=4{\sqrt {3}}}
斯涅尔翻倍法算七次 n = 6 × 2 k {\displaystyle n=6\times 2^{k}} . k {\displaystyle k} n {\displaystyle n} u n {\displaystyle u_{n}} U n {\displaystyle U_{n}} u n + U n 4 {\displaystyle {\frac {u_{n}+U_{n}}{4}}} 0 6 6.0000000 6.9282032 3.2320508 1 12 6.2116571 6.4307806 3.1606094 2 24 6.2652572 6.3193199 3.1461443 3 48 6.2787004 6.2921724 3.1427182 4 96 6.2820639 6.2854292 3.1418733 5 192 6.2829049 6.2837461 3.1416628 6 384 6.2831152 6.2833255 3.1416102 7 768 6.2831678 6.2832204 3.1415970
最后一个数值的一个最佳有理逼近是 355 113 {\displaystyle {\frac {355}{113}}} π {\displaystyle \pi }
n 3 sin π n 2 + cos π n < π < n 2 sin π n + tan π n 3 {\displaystyle n{\frac {3\sin {\frac {\pi }{n}}}{2+\cos {\frac {\pi }{n}}}}<\pi <n{\frac {2\sin {\frac {\pi }{n}}+\tan {\frac {\pi }{n}}}{3}}} 从而我们能得到同样的逼近,从 48 边形算得十进制值约为 3.14159292。
圆和相似三角形:外切边、内接边及其补、内接割线及其补 让我们考虑边长为 s n {\displaystyle s_{n}} n {\displaystyle n} A B {\displaystyle AB} A ′ {\displaystyle A'} A {\displaystyle A} A ′ A {\displaystyle A'A} A ′ A B {\displaystyle A'AB} 泰勒斯定理 ,这是一个直角三角形,角 B {\displaystyle B} A ′ B {\displaystyle A'B} c n {\displaystyle c_{n}} s n {\displaystyle s_{n}} c n 2 + s n 2 = ( 2 r ) 2 {\displaystyle {c_{n}}^{2}+{s_{n}}^{2}=(2r)^{2}} C {\displaystyle C} A B {\displaystyle AB} C ′ {\displaystyle C'} C {\displaystyle C} C A {\displaystyle CA} s 2 n {\displaystyle s_{2n}} C ′ A {\displaystyle C'A} c 2 n {\displaystyle c_{2n}} C ′ C A {\displaystyle C'CA} C ′ C {\displaystyle C'C} C {\displaystyle C} A B {\displaystyle AB} C ′ C {\displaystyle C'C} A B {\displaystyle AB} P {\displaystyle P} C ′ A P {\displaystyle C'AP} 相似 于 C ′ C A {\displaystyle C'CA} C {\displaystyle C} C ′ A : C ′ C = C ′ P : C ′ A {\displaystyle C'A:C'C=C'P:C'A} A P : C ′ A = C A : C ′ C {\displaystyle AP:C'A=CA:C'C} O {\displaystyle O} A ′ A {\displaystyle A'A} O A P {\displaystyle OAP} A ′ A B {\displaystyle A'AB} O P {\displaystyle OP} A ′ B {\displaystyle A'B}
c 2 n 2 = ( r + 1 2 c n ) 2 r c 2 n = s n s 2 n . {\displaystyle {\begin{aligned}c_{2n}^{2}&{}=\left(r+{\frac {1}{2}}c_{n}\right)2r\\c_{2n}&{}={\frac {s_{n}}{s_{2n}}}.\end{aligned}}} 在第一个等式中 C ′ P {\displaystyle C'P} C ′ O + O P {\displaystyle C'O+OP} r + 1 2 c n {\displaystyle r+{\frac {1}{2}}c_{n}} C ′ C {\displaystyle C'C} 2 r {\displaystyle 2r} 鲁道夫·范·科伊伦 翻倍公式,
c 2 n = 2 + c n . {\displaystyle c_{2n}={\sqrt {2+c_{n}}}.\,\!} 现在如果我们外切一个正 n 边形,边为 A ″ + B ″ {\displaystyle A''+B''} A B {\displaystyle AB} O A B {\displaystyle OAB} O A ″ B ″ {\displaystyle OA''B''} A ″ B ″ : A B = O C : O P {\displaystyle A''B'':AB=OC:OP} S n {\displaystyle S_{n}} S n : s n = 1 : 1 2 c n {\displaystyle S_{n}:s_{n}=1:{\frac {1}{2}}c_{n}} O P {\displaystyle OP} A ′ B {\displaystyle A'B}
c n = 2 s n S n . {\displaystyle c_{n}=2{\frac {s_{n}}{S_{n}}}.\,\!} 称外切周长为 u n = n s n {\displaystyle u_{n}=ns_{n}} U n = n S n {\displaystyle U_{n}=nS_{n}}
c 2 n = s n s 2 n = 2 s 2 n S 2 n , {\displaystyle c_{2n}={\frac {s_{n}}{s_{2n}}}=2{\frac {s_{2n}}{S_{2n}}},} 所以
u 2 n 2 = u n U 2 n . {\displaystyle u_{2n}^{2}=u_{n}U_{2n}.\,\!} 给出一个几何平均 等式。
同样我们也推出
2 s 2 n S 2 n s n s 2 n = 2 + 2 s n S n , {\displaystyle 2{\frac {s_{2n}}{S_{2n}}}{\frac {s_{n}}{s_{2n}}}=2+2{\frac {s_{n}}{S_{n}}},} 或
2 U 2 n = 1 u n + 1 U n . {\displaystyle {\frac {2}{U_{2n}}}={\frac {1}{u_{n}}}+{\frac {1}{U_{n}}}.} 给出一个调和平均 等式。
蒙特卡罗方法求圆面积。由这 900 个样本算得 4×709 ⁄900 = 3.15111. 当更好的方法寻找圆的面积无效时,我们可以求助于“掷飞镖”。这种蒙特卡罗算法 的原理是:如果随机样本一致地散布于一个包含圆的正方形中,样本击中圆的比例趋近于圆和正方形的面积比。这可以视为求圆(或任何区域)面积的最后一种手段,因为它要求巨大的样本数才能确保精确度,一个 10−n 的估计需要大约 100n Thijsse 2006 ,p. 273)。在某些情形,蒙特卡罗算法是数值逼近可用的最好方法。
我们已经看到可以将圆分为无穷块重组为一个长方形。最近(Laczkovich 1990 )发现的一个惊人的事实是我们可以将圆分为很大但有限 块然后重拼成一个相同面积的正方形。这称为塔斯基分割圆问题 。米可斯·拉茲柯維奇 的证明本质是他证明了“存在”这样的分解(事实上有很多),但是没有给出任何实际的分解。
我们可以将圆伸缩长为一个椭圆 。因为伸缩是一个平面的线性变换 ,一个变形因子会改变面积但是保持面积的比例。这个观察可以用于从单位圆得出任何椭圆的面积。
考虑单位圆内切于边长为 2 的正方形。一个伸长或收缩分别把水平与垂直半径变为椭圆的半长轴 与半短轴 。正方形变为一个外切于椭圆的长方形。圆与正方形面积比为 π 4 {\displaystyle {\frac {\pi }{4}}} π 4 {\displaystyle {\frac {\pi }{4}}} a {\displaystyle a} b {\displaystyle b} 4 a b {\displaystyle 4ab} π a b {\displaystyle \pi ab}
我们也可以考虑高维数类似测度,比如可能想要求出球体 的体积。当我们知道球面面积公式后,可以使用与圆一样的“洋葱”积分法。
^ 中文的“圆”可以指圆周(circle)也能指圆盘(disk),此文中“圆”指圆盘。 Archimedes , Measurement of a circle, T. L. Heath (trans.) (编), The Works of Archimedes , Dover : 91–93, 260 BCE, ISBN 978-0-486-42084-4 Cambridge University Press , 1897, based on J. L. Heiberg's Greek version.)Beckmann, Petr, A History of Pi, St. Martin's Griffin , 1976, ISBN 978-0-312-38185-1 Gerretsen, J.; Verdenduin, P., Chapter 8: Polygons and Polyhedra, H. Behnke, F. Bachmann, K. Fladt, H. Kunle (eds.), S. H. Gould (trans.) (编), Fundamentals of Mathematics, Volume II: Geometry, MIT Press : 243–250, 1983, ISBN 978-0-262-52094-2 Grundzüge der Mathematik , Vandenhoeck & Ruprecht, Göttingen, 1971.)Laczkovich, Miklós , Equidecomposability and discrepancy: A solution to Tarski's circle squaring problem , Journal für die reine und angewandte Mathematik (Crelle’s Journal ), 1990, 404 : 77–117, ISSN 0075-4102 [失效連結 Lange, Serge , The length of the circle, Math! : Encounters with High School Students, Springer-Verlag , 1985, ISBN 978-0-387-96129-3 Smith, David Eugene ; Mikami, Yoshio, A history of Japanese mathematics , Chicago: Open Court Publishing : 130–132, 1914, ISBN 978-0-87548-170-8 Thijsse, J. M., Computational Physics, Cambridge University Press: p. 273, 2006, ISBN 978-0-5215-7588-1 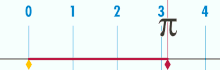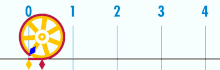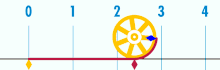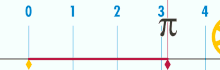








 French
French Deutsch
Deutsch





























![{\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=\left[(2\pi ){\frac {t^{2}}{2}}\right]_{t=0}^{r}\\&{}=\pi r^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7732a8e7d081596042d1a4f09556b2ad246bfbfd)









![{\displaystyle =2r^{2}\left[\theta +{\frac {1}{2}}\sin 2\theta \right]_{0}^{\frac {\pi }{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8314266b45dedf7f687244018044ca64a3e38d3b)



























































