日震學 - 维基百科,自由的百科全书
此條目翻譯品質不佳。 (2024年7月4日) |

日震學(英語:Helioseismology)是研究波振盪,特別是聲波壓力,在太陽上的傳播。不同於地球的地震波,太陽的波幾乎沒有剪力的成份 (S波)。太陽壓力波被認為是接近太陽表面的對流層中的湍流生成的[1]。有些頻率被建設性的干涉放大,換言之,太陽振盪的環像是一個鐘,聲波傳輸到太陽更表面的光球層,這是從太陽中心的核融合輻射出的能量經由吸收生成可見光,離開太陽表面的區域。這些振盪幾乎在任何時間序列的太陽影像上都能檢測得到,但觀測到最好的影像是測量都卜勒位移的光球吸收譜線。經由太陽振盪波的傳播的變化,揭露了太陽內部的結構,並讓天文物理學家發展出太陽內部剖面極為詳細的設定條件。
日震學可以排除太陽微中子問題是由於太陽內部模型不正確的可能性[2] 日震學揭示的特性包括外側的對流層和內側的輻射層以不同的速度旋轉,這引發太陽發電機產生磁場效應的想法[3][4],和在太陽表面對流層下的數千公里有電漿"噴射氣流" (更明確的說,扭轉振盪) [5]。這些噴射氣流從赤道廣泛的散播,在高緯度地區分解成小旋風的風暴。扭轉振盪是太陽較差自轉時間的變化,它們的交錯影響旋轉快與慢的帶。這是我們在1980年就已經發現的,但到目前為止,還沒有理論能解釋並被普遍的接受,即使它們與太陽週期的密切關係很明顯,一樣有著11年的周期[6]。
日震學也可以用來生成太陽背面的影像,包括從地球看不到的太陽黑子影像[7]。簡單來說,太陽黑子會吸收日震波 。這種太陽黑子的吸收會在太陽黑子的對蹠點上造成震波虧損的影像[8]。為方便太空氣象的預測,從2000年晚期,經由SOHO衛星就有部分太陽背面中央地區的日震影像圖不停的被產生,而從2001年起,全部的背面影像都被生成和進行資料分析。
日震学的名稱源自類似研究地震波以確定地球內部結構的地震学。日震学可以和星震學對照,后者是研究一般恆星振荡的学科。
太陽振盪的類型
[编辑]
在太陽的個別振盪會受到阻尼,所以經過幾個週期就會消失。但是,當這些地區性擾動的干涉產生全球性的駐波,也就所謂的簡正模式。分析這些重疊模式構成球面日震學的規律。
基於驅動它們的恢復力:聲學的、重力、和表面重力,太陽振盪模是基本上分為三種類型:
- p-模式或聲波有壓力作為它們的恢復力,因此稱為p-模式。在太陽內部的聲速取決於其動力學。P-模式振盪的頻率大於1mHz,並且在2-4mHz的範圍最強,它們通常被稱為5分鐘振盪 (註:5分鐘振盪的頻率是每秒鐘1/300週期 = 3.33mHz)。p-模式在太陽表面有數百公里的振幅,並且隨時可以從都卜勒影像或靈敏度較高的譜線強度成像檢測出來。數以千計的高和中等強度的I級數p-模式 (見下文的波數級I) 已經被搭載在SOHO衛星上的邁克爾遜都卜勒影像器 ( Michelson Doppler Imager,MDI) 檢測到,I強度低於200的明顯的和記再一起形成脊的高強度模式分隔開來[9]。SOHO衛星搭載的GOLF大約偵測到10個頻率低於1.5mHz的p-模式[10]。
- g-模式或重力波 是密度波,以引力 (負浮力的取代物質) 作為恢復力,因此稱為"g-模式"。g-模式的振盪是低頻波 (0-0.4mHz),他們侷限在太陽內部的對流層內 (從0.7延伸至1.0太陽半徑),實際上在太陽表面是看不見的。恢復力是由絕熱膨脹引起的:在太陽內部的深處,溫度梯度是微弱的,因而只有少量比周圍的環境較冷和密度較高的氣泡會移動 (例如向上),並且將會因此被拉回原來的位置;這種恢復力驅動的是g-模式。在太陽的對流層,溫度梯度略大於絕熱遞減率,所以有一個反恢復力 (即對流驅動器) 使得g-模式不能傳播。通過整個對流層的g-模式是倏逝的,並被認為在光球上殘餘的振幅只有數毫米,但仍比溫度擾動更為顯著 (突出)[11]。從80年代起,有數起聲稱測得g-模式,但都無法確認。在2007年,據稱使用GOLF測得一次g-模式[12]。GONG2008 / SOHO XXI在波爾德舉行會議,腓比斯集團的報告不能证实此一研究結果,認為g-模式振幅的上限是3mm/s,未達到GOLF能夠測量的限制。最後,腓比斯集團發表了剛剛審查g-模式的回顧和目前對太陽g-模式的了解狀態[13]。
- f-模式或表面重力波是一種重力波,但是只發生在光球或是光球的附近,而且該處的溫度梯度再次低於絕熱遞減率。有些中和高程度的f-模式,介於l = 117 和 l = 300之間 (見下文的波數級I),曾經被MDI檢測到[14]。
振盪資料分析
[编辑]來自太陽光譜的時間系列顯示所有的振盪是重疊的,成千上萬的模式已經被檢測(真實的數字也許是數以百萬計)。數學技術中的傅立葉分析被用來將這一大堆的資料恢復為個別模式的資訊。這個想法是任何的週期函數f可以寫成最簡單的週期函數的總合,也就是不同頻率的正弦和餘弦倍數的結合。要找出有多少個這種簡單的函數 (振幅) 結合成f,一個適用的傅立葉轉換:在每個點上經由特定的積分函數計算獲得的值再加入f的修訂版本。
最簡單的分析模式是徑向的;不過大多數的太陽模型是非徑向的。一個非徑向模型的特徵是三個波數:球諧度 I 和方位順序 m,這是用來測定恒星表面上的行為模式,和徑向狀態 n,反映了在徑向方面的屬性 (例子見圖的右上方)。請注意,太陽如果是球對稱,方位順序將呈現衰退;但是,太陽的自轉 (連同其它的擾動) 導致赤道突起,增加了此種衰退。依照規律,n對應於徑向本徵函數節點的數目,I 表是在球面上結線的總數,m 告訴我們有多少的節點線跨越了赤道。
恆星震盪的頻率通常取決於波的所有這三個數值。它是很方便的,然而,分離這些頻率成為多種頻率,得到一個適當的超越方位等級m,對應於恆星球對稱的結構,和頻率分裂。
振盪資料的分析必須嘗試單獨分離出這些不同頻率的元件。在太陽的情況下,可以直接觀察到在太陽盤面上的振盪是位置與時間的函數,因此在這兒可以分析其在空間的屬性。這可以在將太陽表面的位置通過2維傅立葉轉換歸納的手段,分離出特定的l和m的數值,接著由在時間的傅立葉轉換中分離該頻率類型的模式。事實上,對恆星表面上的觀測隱含著恆星振盪的平均值,可以看成是這種傅立葉轉換空間的一種例子。
請注意這些振盪的資料,毋寧是連續函數,而不是等同於在網格中的時間和位置受到實驗誤差計算約束的值。當轉換計算時,這些函數的值再網格外以近似值有限的插入和積分,無可避免的是會進一步引進誤差的過程。詳細數值的使用方法包括轉換資料的目地對照和抑制誤差。
這些論述整理自約爾根·克里斯滕森-達斯加特對恆星振盪演講的筆記[15]。
反演
[编辑]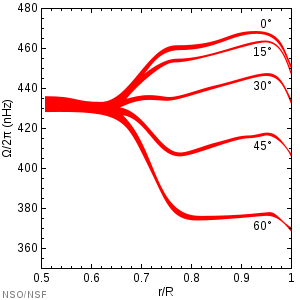
有關日震波資訊的 (像是模式下的頻率和頻率分割) 收集在經過轉換這些振動資料可用於推斷太陽內部詳細的數值特性,例如內部的聲速、在太陽裡面的內部較差自轉。像是積分與方程式和分析的關聯性可以巧妙的處理資料轉換所涉及的內部屬性期望。使用的數值方法都適用於內部獨特的檢驗,以最大數量的資訊,以最少的誤差,提取有關內部功能的振盪。此一過程被稱為日震反演。
一個有較多細節的例子,與振盪頻率分割相關的,通過積分可以得到在太陽內部的角速度。[15]
內部結構
[编辑]日震學的觀測揭露了內部不一致的轉動層和不同轉動的太陽殼層,大約各自對應於輻射和對流層[3]。參看右測顯示的關係圖,這個過渡層稱為差旋層。
日震学的应用
[编辑]日震學的研究可以推斷太陽的年齡[16]。這是因為在太陽深處的聲波傳遞取決於組成,尤其是核心的氫和氦的相對豐度。由於太陽在生命期中不斷的將氫融合成氦,因此將恆星演化的數值模型使用於太陽 (標準太陽模型),可以用目前在核心的氦豐度推斷出太陽的年齡。這種方法為從收集的隕石所推測的太陽年齡提供了證明[17]。
區域日震學
[编辑]噴射氣流運動可能會影響太陽週期
[编辑]內部的噴射氣流運動落後於時程表,或許可以解釋2009年太陽周期開始的延遲[18]。
相關條目
[编辑]參考資料
[编辑]- ^ Goldreich, P.; Keeley, D.A. Solar seismology. II - The stochastic excitation of the solar p-modes by turbulent convection. Astrophysical Journal. February 1977, 212: 243–251. Bibcode:1977ApJ...212..243G. doi:10.1086/155043.
- ^ Bahcall, J.N.; Pinsonneault, M.H.; Basu, S.; Christensen-Dalsgaard, J. Are Standard Solar Models Reliable?. Physical Review Letters. January 1997, 78 (2): 171–174. Bibcode:1997PhRvL..78..171B. arXiv:astro-ph/9610250
 . doi:10.1103/PhysRevLett.78.171.
. doi:10.1103/PhysRevLett.78.171. - ^ 3.0 3.1 Thompson, M.J.; Christensen-Dalsgaard, J.; Miesch, M.S.; Toomre, J. The Internal Rotation of the Sun. Annual Review of Astronomy & Astrophysics. 2003, 41 (1): 599–643. Bibcode:2003ARA&A..41..599T. doi:10.1146/annurev.astro.41.011802.094848.
- ^ Ossendrijver, M. The solar dynamo. The Astronomy and Astrophysics Review. 2003, 11 (4): 287–367. Bibcode:2003A&ARv..11..287O. doi:10.1007/s00159-003-0019-3.
- ^ Vorontsov, S.V.; Christensen-Dalsgaard, J.; Schou, J.; Strakhov, V.N.; Thompson, M.J. Helioseismic Measurement of Solar Torsional Oscillations. Science. April 2002, 296 (5565): 101–103. Bibcode:2002Sci...296..101V. PMID 11935019. doi:10.1126/science.1069190.
- ^ Howard, R.; Labonte, B.J. The sun is observed to be a torsional oscillator with a period of 11 years. Astrophysical Journal. July 1980, 239: L33–L36. Bibcode:1980ApJ...239L..33H. doi:10.1086/183286.
- ^ Braun, D.C.; Lindsey, C. Seismic Imaging of the Far Hemisphere of the Sun. The Astrophysical Journal. October 2001, 560 (2): L189–L192. Bibcode:2001ApJ...560L.189B. doi:10.1086/324323.
- ^ Lindsey, C.; Braun, D.C. Helioseismic imaging of sunspots at their antipodes. Solar Physics. March 1990, 126 (1): 101–115. Bibcode:1990SoPh..126..101L. doi:10.1007/BF00158301.
- ^ Rabello-Soares, M.C.; Korzennik, S.G.; Schou, J. The determination of MDI high-degree mode frequencies. ESA Special Publication 464: 129–136. January 2001. Bibcode:2001ESASP.464..129R.
|booktitle=被忽略 (帮助) - ^ Garcia, R.A.; Regulo, C.; Turck-Chieze, S.; Bertello, L.; Kosovichev, A.G.; Brun, A.S.; Couvidat, S.; Henney, C.J.; Lazrek, M.; Ulrich, R.K.; Varadi, F. Low-Degree Low-Order Solar p Modes As Seen By GOLF On board SOHO. Solar Physics. May 2001, 20: 361–379. Bibcode:2001SoPh..200..361G.
- ^ Randall J. Bos; Henry A. Hill. Detection of individual normal modes of oscillation of the Sun in the period range from 2 hr to 10 min in solar diameter studies. Solar Physics. January 1983, 82 (1-2): 89-102 (英语).[永久失效連結]
- ^ Garcia, R.A.; Turck-Chieze, S.; Jimenez-Reyes, S.J.; Ballot, J.; Palle, P.L.; Eff-Darwich, A.; Mathur, S.; Provost, J. Tracking Solar Gravity Modes: The Dynamics of the Solar Core. Science. June 2007, 316 (5831): 1591–. Bibcode:2007Sci...316.1591G. PMID 17478682. doi:10.1126/science.1140598.
- ^ Appourchaux, T.; et al. The quest for the solar g modes. October 2009. Bibcode:2009arXiv0910.0848A. arXiv:0910.0848
 [astro-ph.SR]. cite arXiv模板填写了不支持的参数 (帮助)
[astro-ph.SR]. cite arXiv模板填写了不支持的参数 (帮助) - ^ Corbard, T.; Thompson, M.J. The subsurface radial gradient of solar angular velocity from MDI f-mode observations. Solar Physics. February 2002, 205 (2): 211–229. Bibcode:2002SoPh..205..211C. arXiv:astro-ph/0110361
 . doi:10.1023/A:1014224523374.
. doi:10.1023/A:1014224523374. - ^ 15.0 15.1 Christensen-Dalsgaard, J., 2003, Lecture Notes on Stellar Oscillations. Fifth Edition (页面存档备份,存于互联网档案馆), lecture notes, University of Aarhus. Retrieved November 2009.
- ^ A. Bonanno, H. Schlattl, L. Paternò. The age of the Sun and the relativistic corrections in the EOS. Astronomy and Astrophysics. 2002, 390 (3): 1115. Bibcode:2002A&A...390.1115B. arXiv:astro-ph/0204331
 . doi:10.1051/0004-6361:20020749.
. doi:10.1051/0004-6361:20020749. - ^ Guenther, D.B. Age of the sun. Astrophysical Journal. April 1989, 339: 1156–1159. Bibcode:1989ApJ...339.1156G. doi:10.1086/167370.
- ^ Anne Minard. The Case of the Missing Sunspots: Solved?. June 17, 2009 [2014-04-09]. (原始内容存档于2010-03-10) (英语).
外部連結
[编辑]- Non-technical description of helio- and asteroseismology retrieved November 2009
- Laurent Gizon and Aaron C. Birch, "Local Helioseismology", Living Rev. Solar Phys. 2 (2005) 6 online article
- Scientists Issue Unprecedented Forecast of Next Sunspot Cycle (页面存档备份,存于互联网档案馆) National Science Foundation press release, March 6, 2006
- Large-Scale Dynamics of the Convection Zone and Tachocline (页面存档备份,存于互联网档案馆) by Mark S. Miesch
- European Helio- and Asteroseismology Network (HELAS)
- Farside and Earthside images of the Sun (页面存档备份,存于互联网档案馆)
- Living Reviews in Solar Physics (页面存档备份,存于互联网档案馆)


 French
French Deutsch
Deutsch


