自旋玻璃 - 维基百科,自由的百科全书
| 凝聚态物理学 |
|---|
 |
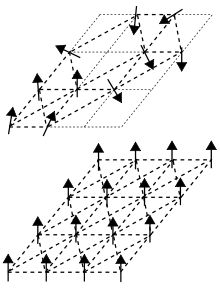
自旋玻璃是磁性合金材料的一种亚稳定的状态。铁磁性状态和反铁磁性状态中,磁矩的磁矩方向(自旋)的分布是长程有序的,而自旋玻璃状态中的磁矩方向是随机冻结的,其分布呈现出长程无序性。这里的“玻璃”实际上是长程无序状态的代名词,指这种无序状态类似于一般所说的玻璃。
自旋玻璃表现出的众多亚稳定结构,使得它具有明显的磁化弛豫现象,这也使得实验和模拟自旋玻璃的难度加大。
简介
[编辑]磁性材料是由许多具有稳定磁矩的原子或小原子集团构成的,它们的磁矩之间相互作用,构成了宏观上的磁性现象。这样的相互作用基本有两类。一类是铁磁相互作用:两个相邻的磁矩排成同一个方向。另一类是反铁磁相互作用:相邻的磁矩排成相反的方向。如果材料的内部只有铁磁相互作用,所有的磁矩排成了同一个方向,那么材料具有像磁铁一样的性质。如果只有反铁磁相互作用,那么磁矩的方向总是正反相间,相互抵消,磁化率为0。宏观上,材料“没有磁性”。而当材料内部随机存在着铁磁相互作用和反铁磁相互作用时,就会形成自旋玻璃。
自旋玻璃材料
[编辑]最早被研究的自旋玻璃材料是一些稀磁合金,即将少量磁性金属掺杂到非磁性金属中得到的合金,比如铜掺锰合金Cu1-xMnx与金掺铁合金Au1-xFex。其中是表示掺杂金属的比例。
物理特性
[编辑]自旋玻璃材料的发现,是因为它与一般的铁磁性和反铁磁性等材料有着不同的物理特性。
自旋冻结
[编辑]相互作用产生有序,热运动产生无序。当物质的温度升高时,原子自身的热运动逐渐超过原子之间的相互作用,于是物质宏观上变为顺磁性。而当温度重新降低时,物质将恢复独自的磁性特质。铁磁体材料在高温状态下的磁性特征遵从居里-外斯定律。而当温度降至一定水平(称为相变温度或居里点)后,将快速恢复铁磁性性质。而自旋玻璃材料在高温时虽然也呈现顺磁性,但当温度下降时,复杂的相互作用使得长程有序状态无法形成,各个磁矩被随机地冻结在某个方向,最后呈现无规则的长程无序状态。而这个转变过程是缓和的,就磁化率(测量宏观上磁性到底有多大的量)来说,自旋玻璃材料在温度下降时磁化率先缓慢增高,经过一个峰值后再缓慢下降[1]:3。达到峰值时的温度也称为“冻结温度”(表示之后开始“冻结”)。
亚稳态
[编辑]铁磁性材料和反铁磁性材料的磁矩在相变温度以下只有一种排列状态。比如铁磁性材料在低温时所有的磁矩都按着同一个方向排列。这个状态下系统的能量是最低的。要改变这种状态需要较大的能量。而自旋玻璃材料在低温时可能出现很多种不同的状态,这些状态下系统的能量都差不多(差距极微小),被称为亚稳态。这种情况的出现是由于所谓的“阻挫现象”(frustration,或称受挫现象)。
阻挫
[编辑]
阻挫现象是对自旋玻璃态系统中亚稳基态众多的解释,其含义是由于几何结构使得不存在一个确定的磁矩(自旋)状态能满足系统能量最小化的要求[2]:89。最简单的例子是一个由三个自旋组成的系统,每两个自旋之间都是反磁相互作用。当其中两个自旋方向相反(一上一下)的时候,无论第三个自旋处于什么状态(上或者下),都无法满足所有相互作用的要求:两种状态的系统能量相同[2]:90。因此,这两种状态出现的可能性是一样大的,这就是阻挫。当这类三自旋系统或类似的系统数量众多的时候,会有很多个不同的状态有着几乎同样的能量,这导致了自旋玻璃材料的基态的复杂性[3]:12-13。
磁化弛豫
[编辑]自旋玻璃材料由于自旋随机冻结,宏观整体的磁化率是0。然而,自旋玻璃并不像反铁磁性材料一样在低温时对外部磁场产生抵抗,而是像顺磁性材料一样,会被外部磁场磁化。而自旋玻璃不同于顺磁性材料的地方是,它磁化的过程是相对缓慢的。顺磁材料的磁化弛豫时间(从开始到磁化完成的时间)几乎可以忽略不计,但自旋玻璃则需以分钟甚至小时计。同样地,已经磁化后撤除外部磁场,自旋玻璃需要的恢复时间也是缓慢的。
数学模型
[编辑]愛德華茲-安德森模型(Edwards–Anderson model)
[编辑]這模型與易辛模型類似。 在這個模型中,我們將自旋排列在維晶格上,只具有最近鄰相互作用。 該模型可以精確求解臨界溫度,並且觀察到在低溫下存在玻璃相[4]。
谢林顿-柯克帕特里克模型(The model of Sherrington and Kirkpatrick)
[编辑]除了不尋常的實驗特性之外,自旋玻璃也是廣泛的理論和計算研究的主題。 關於自旋玻璃的早期理論工作的很大一部分涉及基於系統配分函數的一組副本的平均場論。
参见
[编辑]参考来源
[编辑]- ^ K. H. Fischer, John Hertz. Spin glasses. Cambridge University Press. 1993. ISBN 9780521447775.
- ^ 2.0 2.1 Prabodh Shukla. Physics of disordered solids. Mittal Publications. 1982, c1981.
- ^ Viktor Dotsenko. An introduction to the theory of spin glasses and neural networks. World Scientific. 1994. ISBN 9789810218737.
- ^ Nishimori, Hidetoshi. Statistical Physics of Spin Glasses and Information Processing: An Introduction. Oxford: Oxford University Press. 2001: 243. ISBN 9780198509400.


 French
French Deutsch
Deutsch


