汤普森构造法 - 维基百科,自由的百科全书
汤普森构造法在计算机科学中是指一个能将正则表达式转化为一个与之等价的非确定有限状态自动机(NFA)的算法。算法得到的NFA可以在编程中用于匹配一个正则表达式,这也是正则表达式引擎实现的基本思路之一。
正则表达式和非确定有限状态自动机是形式语言的两种不同的抽象表达方式。在诸如文本编辑器的高级“查找和替换”以及许多编程语言中,人们都习惯使用正则表达式来表示字符串的匹配模式。然而,当计算机执行匹配程序时,NFA却是更加适合的一种格式。因此,汤普森构造法有着重要的应用价值,它实际上可以视作正则表达式到NFA的一个编译器。而从理论角度上来说,该算法实际上是正则表达式和NFA等价性证明的一部分——事实上,这两种表述形式本质上都对应着相同的语言,即正则语言。
在应用中,算法得到的NFA可以再次通过幂集构造和最小化的过程得到一个对应的最简的确定有限状态自动机(DFA),进而用于匹配正则表达式。但是有些情况下也会直接使用对应的NFA。
算法介绍
[编辑]构造规则
[编辑]算法通过递归地将一个正则表达式划分成构成它的子表达式,在得到每个子表达式对应的NFA之后,根据子表达式之间的运算关系和一系列规则构造表达式自身对应的NFA。[1]具体来说,这套构造规则如下所示[2] :
递归终点
[编辑]对于正则表达式为ε或者只由一个符号构成的情况,则无需继续递归,对应的NFA可以直接由下列规则给出:
空表达式ε直接转化为:
字母表中的单个符号a直接转化为:
子表达式运算的构造规则
[编辑]下面针对正则表达式的三种运算——并、连接和Kleene*闭包给出NFA的构造规则。设子表达式为s和t,则它们对应的NFA分别记作N(s)和N(t)。
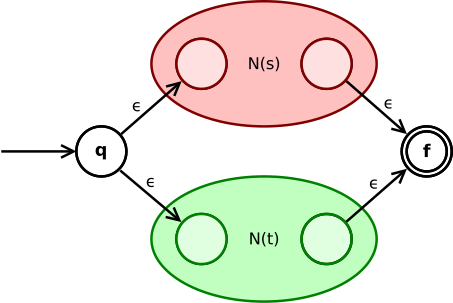
两个正则表达式的并s|t可以转化为:
通过ε转移, 状态q 可以直接到达N(s)或N(t)的初态。而N(s)或N(t)原来的终态也可以通过ε转移直接到达整个NFA的新终态。
连接表达式st可以转化为:
N(s)的初态成为新的NFA的初态。 原来N(s)的终态成为N(t)的初态。而原来N(t)的终态成为新的NFA的终态。
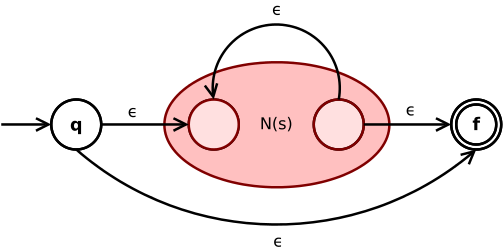
Kleene*闭包s*可以转化为:
将新表达式的初态和终态以及夹在中间的子表达式的NFA N(s)连接起来的ε转移使得可以选择经过或者不经过子表达式。而从N(s)的终态到初态的ε转移使得s可以重复任意多次。
- 加括号的表达式 (s) 直接转化为 N(s) 自身即可。
参考资料
[编辑]- ^ Ken Thompson. Programming Techniques: Regular expression search algorithm. Communications of the ACM. Jun 1968, 11 (6): 419–422. doi:10.1145/363347.363387.
- ^ Alfred V. Aho, Ravi Sethi, Jeffrey Ullman: Compilers: Principles, Techniques and Tools. Addison Wesley, 1986


 French
French Deutsch
Deutsch