Beta-Verteilung – Wikipedia

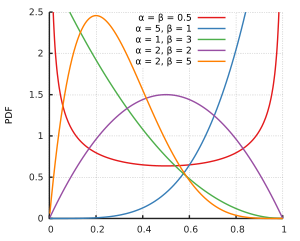
Die Beta-Verteilung ist eine Familie stetiger Wahrscheinlichkeitsverteilungen über dem Intervall ${\displaystyle (0,1)}$, parametrisiert durch zwei Parameter, die häufig als p und q – oder auch als α und β – bezeichnet werden. In der bayesschen Statistik ist die Beta-Verteilung die konjugierte a-priori-Wahrscheinlichkeitsverteilung für die Bernoulli-, Binomial-, der negativen Binomial- und der geometrischen Verteilung.

Die Beta-Verteilung ${\displaystyle \operatorname {Beta} (p,q)}$ ist definiert durch die Wahrscheinlichkeitsdichte

${\displaystyle f(x)={\frac {1}{\mathrm {B} (p,q)}}x^{p-1}(1-x)^{q-1}.}$

Außerhalb des Intervalls ${\displaystyle (0,1)}$ wird sie durch ${\displaystyle f(x)=0}$ fortgesetzt. Für ${\displaystyle p,q\geq 1}$ lässt sich ${\displaystyle (0,1)}$ durch ${\displaystyle [0,1]}$ ersetzen. Die Beta-Verteilung besitzt die reellen Parameter ${\displaystyle p}$ und ${\displaystyle q}$ (in den nebenstehenden Grafiken ${\displaystyle \alpha }$ und ${\displaystyle \beta }$). Um ihre Normierbarkeit zu garantieren, wird ${\displaystyle p,q>0}$ (bzw. ${\displaystyle \alpha ,\beta >0}$) gefordert.

Der Vorfaktor ${\displaystyle 1/\mathrm {B} (p,q)}$ dient der Normierung. Der Ausdruck

${\displaystyle \mathrm {B} (p,q)={\frac {\Gamma (p)\Gamma (q)}{\Gamma (p+q)}}=\int _{0}^{1}u^{p-1}(1-u)^{q-1}\,\mathrm {d} u}$

steht für die Betafunktion, nach der die Verteilung benannt ist. Dabei bezeichnet ${\displaystyle \Gamma }$ die Gammafunktion.

Die Verteilungsfunktion ist entsprechend

${\displaystyle F(x)={\begin{cases}0&{\text{für}}\;x\leq 0,\\I_{x}(p,q)&{\text{für}}\;0<x\leq 1,\\1&{\text{für}}\;x>1\\\end{cases}}}$

mit

${\displaystyle I_{x}(p,q):={\frac {1}{\mathrm {B} (p,q)}}\int _{0}^{x}u^{p-1}(1-u)^{q-1}\mathrm {d} u.}$

Die Funktion ${\displaystyle I_{x}(p,q)}$ heißt auch regularisierte unvollständige Betafunktion.

Der Erwartungswert berechnet sich zu

${\displaystyle \operatorname {E} (X)={\frac {p}{p+q}}}$.

Der Modus, also die Maximalstelle der Dichtefunktion ${\displaystyle f}$, ist für ${\displaystyle p>1}$, ${\displaystyle q>1}$

${\displaystyle \left(1+{\frac {q-1}{p-1}}\right)^{-1}={\frac {p-1}{p+q-2}}}$.

Die Varianz ergibt sich zu

${\displaystyle \operatorname {Var} (X)={\frac {pq}{(p+q+1)(p+q)^{2}}}}$.

Für die Standardabweichung ergibt sich

${\displaystyle \sigma ={\sqrt {\frac {pq}{(p+q+1)(p+q)^{2}}}}}$.

Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten

${\displaystyle \operatorname {VarK} (X)={\sqrt {\frac {q}{p(p+q+1)}}}}$.

Die Schiefe ergibt sich zu

${\displaystyle \operatorname {v} (X)={\frac {2(q-p){\sqrt {p+q+1}}}{(p+q+2){\sqrt {pq}}}}}$.

Aus der momenterzeugenden Funktion ergibt sich für die k-ten Momente

${\displaystyle \operatorname {E} (X^{k})=\prod _{r=0}^{k-1}{\frac {p+r}{p+q+r}}}$.

Die Beta-Verteilung ist für ${\displaystyle p=q}$ symmetrisch um ${\displaystyle x={\frac {1}{2}}}$ mit der Schiefe ${\displaystyle \operatorname {v} (X)=0}$.

Die momenterzeugende Funktion einer betaverteilten Zufallsgröße lautet

${\displaystyle M_{X}(t)=1+\sum _{n=1}^{\infty }\left(\prod _{k=0}^{n-1}{\frac {p+k}{p+q+k}}\right){\frac {t^{n}}{n!}}}$.

Mit der hypergeometrischen Funktion ${\displaystyle _{1}F_{1}}$ erhält man die Darstellung

${\displaystyle M_{X}(t)={}_{1}F_{1}(p;q;t)}$.

Analog zur momenterzeugenden Funktion erhält man die charakteristische Funktion

${\displaystyle \varphi _{X}(t)={}_{1}F_{1}(p;q;it)}$.

• Für ${\displaystyle p=q=1}$ ergibt sich als Spezialfall die stetige Gleichverteilung.
• Für ${\displaystyle p=q={\frac {1}{2}}}$ ergibt sich als Spezialfall die Arcsin-Verteilung.

• Für ${\displaystyle p\rightarrow 0}$ und konstantes ${\displaystyle q}$ geht die Beta-Verteilung in eine Bernoulli-Verteilung ${\displaystyle \operatorname {Ber} \left(0\right)}$ über (eine entsprechende Zufallsgröße hat dann fast sicher den Wert null). Dasselbe gilt für ${\displaystyle q\rightarrow \infty }$ bei konstantem ${\displaystyle p}$.
• Für ${\displaystyle q\rightarrow 0}$ und konstantes ${\displaystyle p}$ geht die Beta-Verteilung in eine Bernoulli-Verteilung ${\displaystyle \operatorname {Ber} \left(1\right)}$ über (eine entsprechende Zufallsgröße hat dann fast sicher den Wert eins). Dasselbe gilt für ${\displaystyle p\rightarrow \infty }$ bei konstantem ${\displaystyle q}$.

Beides sieht man leicht durch entsprechende Grenzwertbildungen der Formeln für Erwartungswert und Varianz: Der Erwartungswert geht gegen null bzw. eins, die Varianz beide Male gegen null.

Wenn ${\displaystyle X\sim \gamma (p_{1},b)}$ und ${\displaystyle Y\sim \gamma (p_{2},b)}$ unabhängige gammaverteilte Zufallsvariablen sind mit den Parametern ${\displaystyle p_{1},b}$ bzw. ${\displaystyle p_{2},b}$, dann ist die Größe ${\displaystyle {\tfrac {X}{X+Y}}}$ betaverteilt mit Parametern ${\displaystyle p_{1}}$ und ${\displaystyle p_{2}}$, kurz

${\displaystyle \operatorname {Beta} (p_{1},p_{2})\sim {\frac {\gamma (p_{1},b)}{\gamma (p_{1},b)+\gamma (p_{2},b)}}.}$

Sind ${\displaystyle X_{1},X_{2},\dotsc ,X_{n}}$ unabhängige auf ${\displaystyle [0,1]}$ stetig gleich verteilte Zufallsvariable, dann sind die Ordnungsstatistiken ${\displaystyle X_{(1)},X_{(2)},\dotsc ,X_{(n)}}$ betaverteilt. Genauer gilt

${\displaystyle X_{(k)}\sim \operatorname {Beta} (k,n-k+1)}$

für ${\displaystyle k=1,\dotsc ,n}$.

Eine Binomialverteilung, deren Parameter ${\displaystyle p}$ betaverteilt ist, nennt man Beta-Binomialverteilung. Dies ist ein spezieller Fall einer Mischverteilung.

Die Beta-Verteilung kann aus zwei Gammaverteilungen bestimmt werden: Der Quotient ${\displaystyle X=U/(U+V)}$ aus den stochastisch unabhängigen Zufallsvariablen ${\displaystyle U}$ und ${\displaystyle V}$, die beide gammaverteilt sind mit den Parametern ${\displaystyle b}$ und ${\displaystyle p_{u}}$ bzw. ${\displaystyle p_{v}}$, ist betaverteilt mit den Parametern ${\displaystyle p_{u}}$ und ${\displaystyle p_{v}}$. ${\displaystyle U}$ und ${\displaystyle V}$ lassen sich als Chi-Quadrat-Verteilungen mit ${\displaystyle 2p_{u}}$ bzw. ${\displaystyle 2p_{v}}$ Freiheitsgraden interpretieren.

Mit Hilfe der linearen Regression wird eine geschätzte Regressionsgerade ${\displaystyle {\hat {y}}={\hat {\beta }}_{0}+{\hat {\beta }}_{1}x_{i}}$ durch eine „Punktwolke“ mit ${\displaystyle n}$ Wertepaaren ${\displaystyle \{x_{i};y_{i}\}_{i=1,\dots ,n}}$ zweier statistischer Merkmale ${\displaystyle X}$ und ${\displaystyle Y}$ gelegt, und zwar so, dass die Quadratsumme der senkrechten Abstände der ${\displaystyle y_{i}}$-Werte von der Geraden ${\displaystyle {\hat {y}}_{i}}$ minimiert wird.

Die Streuung der Schätzwerte ${\displaystyle {\hat {y}}_{i}}$ um ihren Mittelwert ${\displaystyle {\overline {\hat {y}}}={\overline {y}}}$ kann durch ${\displaystyle \textstyle {\text{SSE}}\equiv \sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}}$ gemessen werden und die Streuung der Messwerte ${\displaystyle y_{i}}$ um ihren Mittelwert kann durch ${\displaystyle \textstyle {\text{SST}}\equiv \sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}$ gemessen werden. Erstere stellt die „(durch die Regression) erklärte Quadratsumme“ (sum of squares explained, kurz: SSE) und letztere stellt die „totale Quadratsumme“ (sum of squares total, kurz: SST) dar. Der Quotient dieser beiden Größen ist das Bestimmtheitsmaß:

${\displaystyle {\mathit {R}}^{2}\equiv {\frac {\text{SSE}}{\text{SST}}}}$.

Die „(durch die Regression) nicht erklärte Quadratsumme“ bzw. die „Residuenquadratsumme“ (residual sum of squares, kurz SSR) ist durch ${\displaystyle \textstyle {\text{SSR}}\equiv \sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}$ gegeben. Durch die Quadratsummenzerlegung ${\displaystyle {\text{TSS}}={\text{ESS}}+{\text{RSS}}}$ lässt sich das Bestimmtheitsmaß auch darstellen als

${\displaystyle {\mathit {R}}^{2}={\frac {\text{SSE}}{{\text{SSE}}+{\text{SSR}}}}}$.

Es ist also betaverteilt. Da das Bestimmtheitsmaß das Quadrat des Korrelationskoeffizienten von ${\displaystyle x}$ und ${\displaystyle y}$ darstellt (${\displaystyle R^{2}=r^{2}}$), ist auch das Quadrat des Korrelationskoeffizienten betaverteilt. Allerdings kann die Verteilung des Bestimmtheitsmaßes beim globalen F-Test durch die F-Verteilung angegeben werden, die tabelliert vorliegt.

Die allgemeine Beta-Verteilung ist definiert durch die Wahrscheinlichkeitsdichte

${\displaystyle f(x)={\frac {1}{B(a,b,p,q)}}(x-a)^{p-1}(b-x)^{q-1},}$

wobei ${\displaystyle a}$ und ${\displaystyle b}$ die obere und untere Grenze des Intervalls sind. Entsprechend ergibt sich die Berechnung von ${\displaystyle B}$ zu

${\displaystyle B(a,b,p,q)=\int _{a}^{b}(u-a)^{p-1}(b-u)^{q-1}\mathrm {d} u={\frac {\Gamma (p)\Gamma (q)}{\Gamma (p+q)}}(b-a)^{p+q-1}.}$

Ist ${\displaystyle X}$ betaverteilt auf dem Intervall ${\displaystyle (0,1)}$ mit Parametern ${\displaystyle p}$, ${\displaystyle q}$, dann ist

${\displaystyle Y=(b-a)X+a}$

betaverteilt auf dem Intervall ${\displaystyle (a,b)}$ mit den gleichen Parametern ${\displaystyle p}$, ${\displaystyle q}$. Ist umgekehrt ${\displaystyle Y}$ betaverteilt auf ${\displaystyle (a,b)}$, dann ist

${\displaystyle X={\frac {Y-a}{b-a}}}$

betaverteilt auf ${\displaystyle (0,1)}$.

Im Dreieckstest werden drei Proben im gleichseitigen Dreieck angeordnet, wobei eine Ecke des gedachten Dreiecks nach oben zeigt. Zwei der drei Proben gehören zum Produkt A und eine Probe gehört zum Produkt B oder umgekehrt. Die Aufgabe des Probanden besteht nun darin, dasjenige Produkt zu finden, das nur einmal vorkommt. Die Wahrscheinlichkeit durch bloßes Raten die richtige Antwort zu geben beträgt ${\displaystyle {\tfrac {1}{3}}}$.

Die Erfolgswahrscheinlichkeiten variieren je nach sensorischen Fähigkeiten. Unter der Annahme, dass kein Proband absichtlich eine falsche Antwort gibt, liegt die Erfolgswahrscheinlichkeit bei niemandem unter ${\displaystyle {\tfrac {1}{3}}}$. Bei Feinschmeckern oder großen Geschmacksunterschieden kann diese theoretisch bis auf 100 % ansteigen. Im Folgenden wird für beliebige Rate-Erfolgswahrscheinlichkeiten ${\displaystyle c}$ mit ${\displaystyle 0<c<1}$ die Beta-Verteilung auf ${\displaystyle (c,1)}$ hergeleitet.^[1] Aus den eben genannten Gründen modelliert diese Wahrscheinlichkeitsdichte die Erfolgswahrscheinlichkeiten der Probanden realistischer als eine Beta-Verteilung auf ${\displaystyle (0,1)}$.

Die Erfolgswahrscheinlichkeiten ${\displaystyle \pi _{i}}$ der einzelnen Probanden ${\displaystyle i=1,\dots ,n}$ seien zunächst betaverteilt auf ${\displaystyle (0,1)}$ mit Parametern ${\displaystyle \alpha }$ und ${\displaystyle \beta }$. Die korrigierten Erfolgswahrscheinlichkeiten auf ${\displaystyle (c,1)}$ ergeben sich aus ${\displaystyle p_{i}=c+(1-c)\pi _{i}}$. Die Wahrscheinlichkeitsdichte von ${\displaystyle p_{i}}$ lässt sich über den Transformationssatz für Dichten bestimmen. Die Beta-Verteilung von ${\displaystyle \pi _{i}}$ hat eine positive Dichte im Intervall ${\displaystyle (0,1)}$. Die Transformation ${\displaystyle u\colon (0,1)\rightarrow (c,1)}$ mit ${\displaystyle u(\pi )=c+(1-c)\pi =p}$ ist ein Diffeomorphismus. Daraus erhält man die Umkehrfunktion ${\displaystyle u^{-1}(p)={\frac {p-c}{1-c}}}$. Für die gesuchte Dichtefunktion von ${\displaystyle p}$ erhält man

${\displaystyle f_{p}(p)=f_{\pi }(u^{-1}(p))\left|{\frac {\partial }{\partial p}}u^{-1}(p)\right|=f_{\pi }\left({\frac {p-c}{1-c}}\right)\left|{\frac {1}{1-c}}\right|={\frac {1}{1-c}}f_{\pi }\left({\frac {p-c}{1-c}}|\alpha ,\beta \right)}$.

Diese Wahrscheinlichkeitsdichte von ${\displaystyle p}$ auf ${\displaystyle (c,1)}$ wird in Abhängigkeit von der Wahrscheinlichkeitsdichte von ${\displaystyle \pi }$ auf ${\displaystyle (0,1)}$ dargestellt. In der nebenstehenden Grafik ist beispielhaft eine Beta-Verteilung auf ${\displaystyle ({\tfrac {1}{3}},1)}$ mit Parametern ${\displaystyle \alpha =0{,}5}$ und ${\displaystyle \beta =4}$ eingezeichnet. Der Erwartungswert beträgt ${\displaystyle 40{,}7\,\%}$. Die durchschnittliche Erfolgswahrscheinlichkeit liegt damit ${\displaystyle 7{,}4\,\%}$ über der Rate-Erfolgswahrscheinlichkeit von ${\displaystyle 33{,}3\,\%}$.

1. ↑ Brockhoff, Per Bruun. "The statistical power of replications in difference tests." Food Quality and Preference 14.5 (2003): 405-417.

• Sigrid Markstein: Mathematische und rechentechnische Aufbereitung der Betaverteilung 1. Art für technologische Untersuchungen.