Elektrische Impedanz – Wikipedia

Die elektrische Impedanz (von lateinisch impedire „hemmen“, „hindern“), auch Komplexer Widerstand oder Wechselstromwiderstand,^[1][2] ist ein elektrischer Widerstand in der Wechselstromtechnik. Sie gibt bei einem zweipoligen Netzwerkelement und bei Sinusvorgängen das Verhältnis von elektrischer Spannung zur Stromstärke an.^[3] Der Begriff wird insbesondere dann verwendet, wenn zwischen den beiden Größen eine Phasenverschiebung bestehen kann,^[2][4] wodurch sich die Impedanz vom Gleichstromwiderstand unterscheidet.

Die elektrische Impedanz ist eine physikalische Rechengröße^[2] zur Beschreibung

• des Verhaltens eines Bauelementes oder Gerätes (allgemein gesagt eines passiven linearen Zweipols) beim Anliegen eines elektrischen Wechselstroms (siehe auch komplexe Wechselstromrechnung),
• der elektromagnetischen Wellenausbreitung in einer Leitung oder einem Medium (siehe auch Wellenimpedanz). Bei der Wellenausbreitung ist kein konkretes Bauelement an diesem Widerstand beteiligt, weder ein Wirk- noch ein Blindwiderstand.

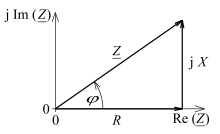
Die elektrische Impedanz wird vorteilhaft als komplexwertige Funktion der Frequenz angegeben. Sie ist die Zusammenfassung von zwei Aussagen:

1. dem Verhältnis der Amplituden von sinusförmiger Wechselspannung und sinusförmigem Wechselstrom und
2. der Verschiebung der Phasenwinkel zwischen diesen beiden Größen.

Beide Eigenschaften werden durch Darstellung der Impedanz als komplexe Größe mathematisch zusammengefasst:

${\displaystyle {\underline {Z}}=|{\underline {Z}}|\cdot e^{\mathrm {j} \varphi }}$, wobei ${\displaystyle \mathrm {j} }$ die imaginäre Einheit ist.

Der Betrag der komplexen Impedanz ${\displaystyle {\underline {Z}}}$ ist der Scheinwiderstand ${\displaystyle Z=|{\underline {Z}}|}$.^[5] Die zeitliche Verschiebung wird durch den Phasenverschiebungswinkel ${\displaystyle \varphi }$ angegeben, der Werte zwischen −90° und +90° annehmen kann. In anderer Schreibweise ist

${\displaystyle {\underline {Z}}=R+\mathrm {j} X\ .}$

Darin ist der Realteil ${\displaystyle R}$ der Anteil der Impedanz, an dem keine Phasenverschiebung auftritt, genannt Wirkwiderstand (Resistanz); dieser ist stets positiv. Der Imaginärteil ${\displaystyle X}$ ist der Anteil, an dem eine Phasenverschiebung um 90° auftritt, genannt Blindwiderstand (Reaktanz); dieser kann positiv oder negativ sein,– positiv dann, wenn die Stromstärke der Spannung nacheilt,– negativ, wenn die Spannung der Stromstärke nacheilt. Der Blindanteil ist frequenzabhängig, der Wirkanteil kann entweder von der Frequenz abhängig oder unabhängig sein; siehe dazu unter Wirkwiderstand oder Elektrischer Widerstand. Jeder ohmsche Widerstand verhält sich wie ein Wirkwiderstand. Eine Umkehrung, wonach sich jeder Wirkwiderstand wie ein ohmscher Widerstand verhält, ist dagegen nicht zulässig. Denn ein ohmscher Widerstand ist definitionsgemäß stets von der Frequenz unabhängig.

Der Kehrwert der Impedanz ist die Admittanz ${\displaystyle {\underline {Y}}}$ (komplexer Leitwert).

Die Begriffswahl in diesem Artikel folgt der Normung, welche festlegt:^[3][6][7][8]

${\displaystyle {\underline {Z}}}$		Impedanz (komplexe Impedanz)
${\displaystyle Z{,}\ |{\underline {Z}}|}$		Scheinwiderstand, Betrag der Impedanz

In der Fachliteratur wird der Begriff Impedanz nicht immer konsequent eingesetzt und synonym sowohl für die komplexe Größe ${\displaystyle {\underline {Z}}}$ als auch für deren Betrag ${\displaystyle Z{,}\ |{\underline {Z}}|}$ verwendet.^[9]

Die Impedanz ist der Quotient aus den Augenblickswerten von komplexer Wechselspannung ${\displaystyle {\underline {u}}}$ und komplexem Wechselstrom ${\displaystyle {\underline {i}}}$. (Zur Darstellung einer Wechselgröße als komplexe Wechselgröße siehe unter Komplexe Wechselstromrechnung.)

${\displaystyle {\underline {Z}}={\frac {\underline {u}}{\underline {i}}}}$

Der Scheinwiderstand ${\displaystyle Z}$ ergibt sich als Quotient aus den Amplituden oder aus den Effektivwerten der reellen Wechselspannung ${\displaystyle u}$ und des reellen Wechselstroms ${\displaystyle i}$

${\displaystyle Z={\frac {\hat {u}}{\hat {\imath }}}={\frac {U_{\mathrm {eff} }}{I_{\mathrm {eff} }}}.}$

Bei der elektromagnetischen Wellenimpedanz werden Spannung und Stromstärke durch andere, entsprechende Größen ersetzt: Die Spannung durch die Feldstärke und die Stromstärke durch die magnetische Flussdichte sowie in der Akustik die Spannung durch den Schalldruck und die Stromstärke durch die Schallschnelle.

Die Impedanz hat Bedeutung bei der Anpassung von Hochfrequenzleitungen, aber auch bei der Wellenausbreitung im freien Raum. Wenn zum Beispiel die Eingangsimpedanz eines Gerätes nicht mit der Impedanz der Leitung übereinstimmt, kommt es zu Reflexionen, was die Leistungsübertragung mindert und was zu Resonanzerscheinungen und damit zu einem nichtlinearen Frequenzgang führen kann.

Elektrodynamische Lautsprecher werden mit Wechselstrom betrieben. Deshalb verursacht der induktive Widerstand der eingebauten Schwingspule eine Phasenverschiebung zwischen Strom und Spannung, die frequenzabhängig ist. Aus diesem Grund wird nicht vom Widerstand gesprochen, sondern von der Impedanz des Lautsprechers.

Werden Impulse durch Kabel übertragen, hat ein ohmscher Widerstand der Leitung geringen Bezug zur Impedanz des Kabels. Hier kommt es fast immer darauf an, Reflexionen der Impulse am entgegengesetzten Ende des Kabels zu vermeiden. Der dazu nötige Abschlusswiderstand ist bei verlustfreien Leitungen praktisch reell, also ein ohmscher Widerstand. Dieser Wert wird als Wellenimpedanz oder Leitungswellenwiderstand des Kabels bezeichnet. Dieser kann abhängig von den Leitungsverlusten bei niedrigen Frequenzen komplexwertig und stark frequenzabhängig werden. Er kann mittels Zeitbereichsreflektometrie bestimmt werden.

In der Biologie kann mittels Electric Cell-Substrate Impedance Sensing die Impedanz genutzt werden, um Formveränderungen bei tierischen Zellen nachzuweisen. Bei In-Vitro-Zellkulturen wird die elektrische Impedanz bei einer festen Frequenz als TEER-Wert angegeben.

Die elektrochemische Impedanzspektroskopie ist eine wichtige Untersuchungsmethode der Elektrochemie, die sowohl in der Grundlagenforschung als auch zur Optimierung verschiedener elektrochemischer Anwendungen (z. B. Energiespeicher wie Batterien oder Brennstoffzellen, elektrochemische Sensoren wie z. B. Sauerstoffsonden) genutzt wird.

Bei Wälzlagern stellt die Wälzlagerimpedanz eine wichtige Messgröße dar, um daraus abgeleitet den Schmierungszustand und mögliche Lagerschäden bewerten zu können.

Die Impedanz hat die Einheit Ohm mit dem Einheitenzeichen Ω. In den zwei Darstellungen als komplexe Größe ${\displaystyle {\underline {Z}}}$ lassen sich ihre Bestandteile und deren Bedeutung ablesen:

• Bei der Formulierung in Polarkoordinaten steht der Betrag ${\displaystyle Z}$ der komplexen Größe ${\displaystyle {\underline {Z}}}$ für den Scheinwiderstand; er ergibt im Zeigerdiagramm die Länge des Zeigers. Die Winkelangabe ${\displaystyle \varphi }$ steht für die Phasenverschiebung zwischen Spannung und Stromstärke; sie ergibt im Zeigerdiagramm die Drehung des Scheinwiderstands gegenüber dem Wirkwiderstand, der auf die reelle Achse gelegt wird:

${\displaystyle {\underline {Z}}=Z\ e^{\mathrm {j} \varphi }=Z\ (\cos \varphi +\mathrm {j} \sin \varphi )\ .}$

• Bei der Formulierung in kartesischen Koordinaten steht der Realteil für den Wirkwiderstand ${\displaystyle R}$, der die übertragene Wirkleistung umsetzt. Der Imaginärteil steht für den Blindwiderstand ${\displaystyle X}$, der keine Wirkleistung umsetzt, sondern Energie speichert und nach einer viertel Periodendauer an den Generator zurückspeist (siehe Blindleistung):

${\displaystyle {\underline {Z}}=R+\mathrm {j} X\ .}$

In einem Zweipol mit einer Induktivität ${\displaystyle L}$ hat diese einen positiven (induktiven) Blindwiderstand ${\displaystyle X=X_{L}=\omega L>0}$; die Spannung eilt dem Strom vor. Dabei steht ${\displaystyle \omega }$ für die Kreisfrequenz der Schwingung. In einem Zweipol mit einer Kapazität ${\displaystyle C}$ hat diese hingegen einen negativen (kapazitiven) Blindwiderstand ${\displaystyle X=X_{C}=-{\frac {1}{\omega C}}<0}$; die Spannung eilt dem Strom nach. (Zur verwendeten Vorzeichenkonvention siehe die Anmerkung zur Konvention unter Blindwiderstand, zur Herleitung siehe unter Komplexe Wechselstromrechnung).

Im Zeigerdiagramm für ${\displaystyle {\underline {Z}}}$ lässt sich ablesen, wie sich die Komponente verhält,

• induktiv: Zeiger im ersten (oberen rechten) Quadranten des Koordinatensystems, positiver Imaginärteil, ${\displaystyle 0<\varphi <\pi /2}$ oder
• kapazitiv: Zeiger im vierten (unteren rechten) Quadranten, negativer Imaginärteil, ${\displaystyle -\pi /2<\varphi <0}$.

Den Scheinwiderstand liefert die pythagoreische Addition der Wirk- und der Blindwiderstände:

${\displaystyle Z={\sqrt {R^{2}+X^{2}}}\ .}$

Bei technischen Geräten wird häufig nur dieser Betrag der Impedanz, also der Scheinwiderstand, angegeben. In einem allgemeinen Netzwerk aus ohmschen Widerständen, Induktivitäten und Kapazitäten ist dieser jedoch frequenzabhängig.

Lautsprecher haben stark frequenzabhängige Impedanzen – es wird jedoch ein Nennwert (z. B. 4 Ω oder 8 Ω) angegeben. Nach internationalem Standard (IEC 60268) darf die im Frequenzbereich vorkommende niedrigste Impedanz diesen Nennwert um nicht mehr als 20 % unterschreiten. Höhere Impedanzen bei anderen Frequenzen sind beliebig zulässig.

Bei Hochfrequenz-Kabeln wird die (bauartbedingte) Kennimpedanz als Wellenwiderstand bezeichnet. Er beträgt bei Koaxialkabeln 50 Ω bis 100 Ω und bei symmetrischen (Zweidraht-)Leitungen 110 Ω bis 300 Ω.

Bei Antennen wird die Eingangsimpedanz auch Fußpunktwiderstand genannt, er sollte bei der Frequenz, für welche die Antenne vorgesehen ist, reell sein und mit der Impedanz des Kabels übereinstimmen (z. B. 60 Ω oder 240 Ω).

Siehe auch: Reflexion bei elektrischen Leitungen, Impedanzanpassung und Wellenimpedanz

Bei der Übertragung von Wechselspannung kommt es zu Reflexionen von Wellen, wenn sich die Impedanz einer Leitung oder des Übertragungsmittels ändert. Dies ist grundsätzlich nicht an die Anzahl der Wellenlängen auf einer Leitung gebunden, bei im Verhältnis zur Wellenlänge kurzen Übertragungswegen wirkt sich aber die Änderung der Impedanz des Übertragungsmittels kaum aus. Am Ort der Impedanzänderung wird ein Teil der ankommenden Welle reflektiert. Der Betrag des Reflexionsfaktors ${\displaystyle r}$ liegt zwischen 0 und 1. Wenn sein Betrag 1 ist, wird die gesamte Welle reflektiert und bei ${\displaystyle r}$ = 0 (das bedeutet ${\displaystyle Z_{1}=Z_{2}}$) tritt keine Reflexion auf, in diesem Fall liegt Impedanzanpassung vor. Diese ist bei Hochfrequenzleitungen und bei der elektromagnetischen Wellenausbreitung oft erwünscht.

${\displaystyle r={\frac {Z_{1}-Z_{2}}{Z_{1}+Z_{2}}}}$

• Jürgen Detlefsen, Uwe Siart: Grundlagen der Hochfrequenztechnik. 2. erweiterte Auflage. Oldenbourg, München u. a. 2006, ISBN 3-486-57866-9.
• Adolf J. Schwab: Elektroenergiesysteme. Erzeugung, Transport, Übertragung und Verteilung elektrischer Energie. Springer, Berlin u. a. 2006, ISBN 3-540-29664-6.
• Wolfgang-Josef Tenbusch: Grundlagen der Lautsprecher. Michael E. Brieden Verlag, Oberhausen 1989, ISBN 3-9801851-0-9 (Klang Ton Edition, 1).
• Gert Hagmann: Grundlagen der Elektrotechnik. 15. Auflage. AULA-Verlag. Wiebelsheim, ISBN 978-3-89104-747-7

Wiktionary: Impedanz – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

1. ↑ Ekbert Hering, Klaus Bressler, Jürgen Gutekunst: Elektronik für Ingenieure und Naturwissenschaftler. 6. Auflage. Springer Vieweg, 2014, S. 264.
2. ↑ ^{a b c} Manfred Albach: Grundlagen der Elektrotechnik 2: Periodische und nicht periodische Signalformen. 2. Auflage. Pearson, 2011, S. 44.
3. ↑ ^{a b} IEC 60050, deutschsprachige Ausgabe bei DKE Deutsche Kommission Elektrotechnik Elektronik Informationstechnik in DIN und VDE: Internationales Elektrotechnisches Wörterbuch, IEV-Nummer 131-12-43.
4. ↑ Dieter Ebner: Technische Grundlagen der Informatik. Springer, 1988, S. 25.
5. ↑ IEC 60050, deutschsprachige Ausgabe bei DKE Deutsche Kommission Elektrotechnik Elektronik Informationstechnik in DIN und VDE: Internationales Elektrotechnisches Wörterbuch, IEV-Nummer 131-12-44.
6. ↑ DIN 1304-1, Formelzeichen, 1994
7. ↑ DIN 5483-3, Zeitabhängige Größen, Komplexe Darstellung sinusförmig zeitabhängiger Größen, 1994
8. ↑ DIN 40110-1, Wechselstromgrößen; Zweileiter-Stromkreise, 1994
9. ↑ Ralf Kories, Heinz Schmidt-Walter: Taschenbuch der Elektrotechnik. 6. Auflage. Harri Deutsch, 2004, ISBN 3-8171-1734-5, S. 123.