Uniform 4-polytope


In geometry, a uniform 4-polytope (or uniform polychoron)[1] is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.
There are 47 non-prismatic convex uniform 4-polytopes. There are two infinite sets of convex prismatic forms, along with 17 cases arising as prisms of the convex uniform polyhedra. There are also an unknown number of non-convex star forms.
History of discovery
[edit]- Convex Regular polytopes:
- 1852: Ludwig Schläfli proved in his manuscript Theorie der vielfachen Kontinuität that there are exactly 6 regular polytopes in 4 dimensions and only 3 in 5 or more dimensions.
- Regular star 4-polytopes (star polyhedron cells and/or vertex figures)
- 1852: Ludwig Schläfli also found 4 of the 10 regular star 4-polytopes, discounting 6 with cells or vertex figures {5/2,5} and {5,5/2}.
- 1883: Edmund Hess completed the list of 10 of the nonconvex regular 4-polytopes, in his book (in German) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder, von dr. Edmund Hess. Mit sechzehn lithographierten tafeln..
- Convex semiregular polytopes: (Various definitions before Coxeter's uniform category)
- 1900: Thorold Gosset enumerated the list of nonprismatic semiregular convex polytopes with regular cells (Platonic solids) in his publication On the Regular and Semi-Regular Figures in Space of n Dimensions. In four dimensions, this gives the rectified 5-cell, the rectified 600-cell, and the snub 24-cell.[2]
- 1910: Alicia Boole Stott, in her publication Geometrical deduction of semiregular from regular polytopes and space fillings, expanded the definition by also allowing Archimedean solid and prism cells. This construction enumerated 45 semiregular 4-polytopes, corresponding to the nonprismatic forms listed below.[3] The snub 24-cell and grand antiprism were missing from her list.[4]
- 1911: Pieter Hendrik Schoute published Analytic treatment of the polytopes regularly derived from the regular polytopes, followed Boole-Stott's notations, enumerating the convex uniform polytopes by symmetry based on 5-cell, 8-cell/16-cell, and 24-cell.[5][6]
- 1912: E. L. Elte independently expanded on Gosset's list with the publication The Semiregular Polytopes of the Hyperspaces, polytopes with one or two types of semiregular facets.[7]
- Convex uniform polytopes:
- 1940: The search was expanded systematically by H.S.M. Coxeter in his publication Regular and Semi-Regular Polytopes.
- Convex uniform 4-polytopes:
- 1965: The complete list of convex forms was finally enumerated by John Horton Conway and Michael Guy, in their publication Four-Dimensional Archimedean Polytopes, established by computer analysis, adding only one non-Wythoffian convex 4-polytope, the grand antiprism.
- 1966 Norman Johnson completes his Ph.D. dissertation The Theory of Uniform Polytopes and Honeycombs under advisor Coxeter, completes the basic theory of uniform polytopes for dimensions 4 and higher.
- 1986 Coxeter published a paper Regular and Semi-Regular Polytopes II which included analysis of the unique snub 24-cell structure, and the symmetry of the anomalous grand antiprism.
- 1998[8]-2000: The 4-polytopes were systematically named by Norman Johnson, and given by George Olshevsky's online indexed enumeration (used as a basis for this listing). Johnson named the 4-polytopes as polychora, like polyhedra for 3-polytopes, from the Greek roots poly ("many") and choros ("room" or "space").[9] The names of the uniform polychora started with the 6 regular polychora with prefixes based on rings in the Coxeter diagrams; truncation t0,1, cantellation, t0,2, runcination t0,3, with single ringed forms called rectified, and bi, tri-prefixes added when the first ring was on the second or third nodes.[10][11]
- 2004: A proof that the Conway-Guy set is complete was published by Marco Möller in his dissertation, Vierdimensionale Archimedische Polytope. Möller reproduced Johnson's naming system in his listing.[12]
- 2008: The Symmetries of Things[13] was published by John H. Conway and contains the first print-published listing of the convex uniform 4-polytopes and higher dimensional polytopes by Coxeter group family, with general vertex figure diagrams for each ringed Coxeter diagram permutation—snub, grand antiprism, and duoprisms—which he called proprisms for product prisms. He used his own ijk-ambo naming scheme for the indexed ring permutations beyond truncation and bitruncation, and all of Johnson's names were included in the book index.
- Nonregular uniform star 4-polytopes: (similar to the nonconvex uniform polyhedra)
- 1966: Johnson describes three nonconvex uniform antiprisms in 4-space in his dissertation.[14]
- 1990-2006: In a collaborative search, up to 2005 a total of 1845 uniform 4-polytopes (convex and nonconvex) had been identified by Jonathan Bowers and George Olshevsky,[15] with an additional four discovered in 2006 for a total of 1849. The count includes the 74 prisms of the 75 non-prismatic uniform polyhedra (since that is a finite set – the cubic prism is excluded as it duplicates the tesseract), but not the infinite categories of duoprisms or prisms of antiprisms.[16]
- 2020-2023: 342 new polychora were found, bringing up the total number of known uniform 4-polytopes to 2191. The list has not been proven complete.[16][17]
Regular 4-polytopes
[edit]Regular 4-polytopes are a subset of the uniform 4-polytopes, which satisfy additional requirements. Regular 4-polytopes can be expressed with Schläfli symbol {p,q,r} have cells of type {p,q}, faces of type {p}, edge figures {r}, and vertex figures {q,r}.
The existence of a regular 4-polytope {p,q,r} is constrained by the existence of the regular polyhedra {p,q} which becomes cells, and {q,r} which becomes the vertex figure.
Existence as a finite 4-polytope is dependent upon an inequality:[18]
The 16 regular 4-polytopes, with the property that all cells, faces, edges, and vertices are congruent:
- 6 regular convex 4-polytopes: 5-cell {3,3,3}, 8-cell {4,3,3}, 16-cell {3,3,4}, 24-cell {3,4,3}, 120-cell {5,3,3}, and 600-cell {3,3,5}.
- 10 regular star 4-polytopes: icosahedral 120-cell {3,5,5/2}, small stellated 120-cell {5/2,5,3}, great 120-cell {5,5/2,5}, grand 120-cell {5,3,5/2}, great stellated 120-cell {5/2,3,5}, grand stellated 120-cell {5/2,5,5/2}, great grand 120-cell {5,5/2,3}, great icosahedral 120-cell {3,5/2,5}, grand 600-cell {3,3,5/2}, and great grand stellated 120-cell {5/2,3,3}.
Convex uniform 4-polytopes
[edit]Symmetry of uniform 4-polytopes in four dimensions
[edit]The 24 mirrors of F4 can be decomposed into 2 orthogonal D4 groups:
|
The 10 mirrors of B3×A1 can be decomposed into orthogonal groups, 4A1 and D3:
|
There are 5 fundamental mirror symmetry point group families in 4-dimensions: A4 = ![]()
![]()
![]()
![]()
![]()
![]()
![]() , B4 =
, B4 = ![]()
![]()
![]()
![]()
![]()
![]()
![]() , D4 =
, D4 = ![]()
![]()
![]()
![]()
![]() , F4 =
, F4 = ![]()
![]()
![]()
![]()
![]()
![]()
![]() , H4 =
, H4 = ![]()
![]()
![]()
![]()
![]()
![]()
![]() .[10] There are also 3 prismatic groups A3A1 =
.[10] There are also 3 prismatic groups A3A1 = ![]()
![]()
![]()
![]()
![]()
![]()
![]() , B3A1 =
, B3A1 = ![]()
![]()
![]()
![]()
![]()
![]()
![]() , H3A1 =
, H3A1 = ![]()
![]()
![]()
![]()
![]()
![]()
![]() , and duoprismatic groups: I2(p)×I2(q) =
, and duoprismatic groups: I2(p)×I2(q) = ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Each group defined by a Goursat tetrahedron fundamental domain bounded by mirror planes.
. Each group defined by a Goursat tetrahedron fundamental domain bounded by mirror planes.
Each reflective uniform 4-polytope can be constructed in one or more reflective point group in 4 dimensions by a Wythoff construction, represented by rings around permutations of nodes in a Coxeter diagram. Mirror hyperplanes can be grouped, as seen by colored nodes, separated by even-branches. Symmetry groups of the form [a,b,a], have an extended symmetry, [[a,b,a]], doubling the symmetry order. This includes [3,3,3], [3,4,3], and [p,2,p]. Uniform polytopes in these group with symmetric rings contain this extended symmetry.
If all mirrors of a given color are unringed (inactive) in a given uniform polytope, it will have a lower symmetry construction by removing all of the inactive mirrors. If all the nodes of a given color are ringed (active), an alternation operation can generate a new 4-polytope with chiral symmetry, shown as "empty" circled nodes", but the geometry is not generally adjustable to create uniform solutions.
| Weyl group | Conway Quaternion | Abstract structure | Order | Coxeter diagram | Coxeter notation | Commutator subgroup | Coxeter number (h) | Mirrors m=2h | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Irreducible | ||||||||||||
| A4 | +1/60[I×I].21 | S5 | 120 | [3,3,3] | [3,3,3]+ | 5 | 10 | |||||
| D4 | ±1/3[T×T].2 | 1/2.2S4 | 192 | [31,1,1] | [31,1,1]+ | 6 | 12 | |||||
| B4 | ±1/6[O×O].2 | 2S4 = S2≀S4 | 384 | [4,3,3] | 8 | 4 | 12 | |||||
| F4 | ±1/2[O×O].23 | 3.2S4 | 1152 | [3,4,3] | [3+,4,3+] | 12 | 12 | 12 | ||||
| H4 | ±[I×I].2 | 2.(A5×A5).2 | 14400 | [5,3,3] | [5,3,3]+ | 30 | 60 | |||||
| Prismatic groups | ||||||||||||
| A3A1 | +1/24[O×O].23 | S4×D1 | 48 | [3,3,2] = [3,3]×[ ] | [3,3]+ | - | 6 | 1 | ||||
| B3A1 | ±1/24[O×O].2 | S4×D1 | 96 | [4,3,2] = [4,3]×[ ] | - | 3 | 6 | 1 | ||||
| H3A1 | ±1/60[I×I].2 | A5×D1 | 240 | [5,3,2] = [5,3]×[ ] | [5,3]+ | - | 15 | 1 | ||||
| Duoprismatic groups (Use 2p,2q for even integers) | ||||||||||||
| I2(p)I2(q) | ±1/2[D2p×D2q] | Dp×Dq | 4pq | [p,2,q] = [p]×[q] | [p+,2,q+] | - | p | q | ||||
| I2(2p)I2(q) | ±1/2[D4p×D2q] | D2p×Dq | 8pq | [2p,2,q] = [2p]×[q] | - | p | p | q | ||||
| I2(2p)I2(2q) | ±1/2[D4p×D4q] | D2p×D2q | 16pq | [2p,2,2q] = [2p]×[2q] | - | p | p | q | q | |||
Enumeration
[edit]There are 64 convex uniform 4-polytopes, including the 6 regular convex 4-polytopes, and excluding the infinite sets of the duoprisms and the antiprismatic prisms.
- 5 are polyhedral prisms based on the Platonic solids (1 overlap with regular since a cubic hyperprism is a tesseract)
- 13 are polyhedral prisms based on the Archimedean solids
- 9 are in the self-dual regular A4 [3,3,3] group (5-cell) family.
- 9 are in the self-dual regular F4 [3,4,3] group (24-cell) family. (Excluding snub 24-cell)
- 15 are in the regular B4 [3,3,4] group (tesseract/16-cell) family (3 overlap with 24-cell family)
- 15 are in the regular H4 [3,3,5] group (120-cell/600-cell) family.
- 1 special snub form in the [3,4,3] group (24-cell) family.
- 1 special non-Wythoffian 4-polytope, the grand antiprism.
- TOTAL: 68 − 4 = 64
These 64 uniform 4-polytopes are indexed below by George Olshevsky. Repeated symmetry forms are indexed in brackets.
In addition to the 64 above, there are 2 infinite prismatic sets that generate all of the remaining convex forms:
- Set of uniform antiprismatic prisms - sr{p,2}×{ } - Polyhedral prisms of two antiprisms.
- Set of uniform duoprisms - {p}×{q} - A Cartesian product of two polygons.
The A4 family
[edit]The 5-cell has diploid pentachoric [3,3,3] symmetry,[10] of order 120, isomorphic to the permutations of five elements, because all pairs of vertices are related in the same way.
Facets (cells) are given, grouped in their Coxeter diagram locations by removing specified nodes.
| # | Name Bowers name (and acronym) | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3 (5) | Pos. 2 (10) | Pos. 1 (10) | Pos. 0 (5) | Cells | Faces | Edges | Vertices | ||||
| 1 | 5-cell Pentachoron[10] (pen) |  | {3,3,3} | (4) (3.3.3) | 5 | 10 | 10 | 5 | |||
| 2 | rectified 5-cell Rectified pentachoron (rap) | 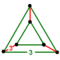 | r{3,3,3} | (3) (3.3.3.3) | (2) (3.3.3) | 10 | 30 | 30 | 10 | ||
| 3 | truncated 5-cell Truncated pentachoron (tip) |  | t{3,3,3} | (3) (3.6.6) | (1) (3.3.3) | 10 | 30 | 40 | 20 | ||
| 4 | cantellated 5-cell Small rhombated pentachoron (srip) |  | rr{3,3,3} | (2) (3.4.3.4) | (2) (3.4.4) | (1) (3.3.3.3) | 20 | 80 | 90 | 30 | |
| 7 | cantitruncated 5-cell Great rhombated pentachoron (grip) | 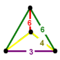 | tr{3,3,3} | (2) (4.6.6) | (1) (3.4.4) | (1) (3.6.6) | 20 | 80 | 120 | 60 | |
| 8 | runcitruncated 5-cell Prismatorhombated pentachoron (prip) |  | t0,1,3{3,3,3} | (1) (3.6.6) | (2) (4.4.6) | (1) (3.4.4) | (1) (3.4.3.4) | 30 | 120 | 150 | 60 |
| # | Name Bowers name (and acronym) | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3-0 (10) | Pos. 1-2 (20) | Alt | Cells | Faces | Edges | Vertices | ||||
| 5 | *runcinated 5-cell Small prismatodecachoron (spid) |  | t0,3{3,3,3} | (2) (3.3.3) | (6) (3.4.4) | 30 | 70 | 60 | 20 | |
| 6 | *bitruncated 5-cell Decachoron (deca) | 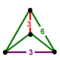 | 2t{3,3,3} | (4) (3.6.6) | 10 | 40 | 60 | 30 | ||
| 9 | *omnitruncated 5-cell Great prismatodecachoron (gippid) |  | t0,1,2,3{3,3,3} | (2) (4.6.6) | (2) (4.4.6) | 30 | 150 | 240 | 120 | |
| Nonuniform | omnisnub 5-cell Snub decachoron (snad) Snub pentachoron (snip)[19] |  | ht0,1,2,3{3,3,3} | (3.3.3.3.3) | (3.3.3.3) | (3.3.3) | 90 | 300 | 270 | 60 |
The three uniform 4-polytopes forms marked with an asterisk, *, have the higher extended pentachoric symmetry, of order 240, [[3,3,3]] because the element corresponding to any element of the underlying 5-cell can be exchanged with one of those corresponding to an element of its dual. There is one small index subgroup [3,3,3]+, order 60, or its doubling [[3,3,3]]+, order 120, defining an omnisnub 5-cell which is listed for completeness, but is not uniform.
The B4 family
[edit]This family has diploid hexadecachoric symmetry,[10] [4,3,3], of order 24×16=384: 4!=24 permutations of the four axes, 24=16 for reflection in each axis. There are 3 small index subgroups, with the first two generate uniform 4-polytopes which are also repeated in other families, [1+,4,3,3], [4,(3,3)+], and [4,3,3]+, all order 192.
Tesseract truncations
[edit]| # | Name (Bowers name and acronym) | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3 (8) | Pos. 2 (24) | Pos. 1 (32) | Pos. 0 (16) | Cells | Faces | Edges | Vertices | |||||
| 10 | tesseract or 8-cell Tesseract (tes) |  | {4,3,3} | (4) (4.4.4) | 8 | 24 | 32 | 16 | ||||
| 11 | Rectified tesseract (rit) | 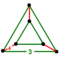 | r{4,3,3} | (3) (3.4.3.4) | (2) (3.3.3) | 24 | 88 | 96 | 32 | |||
| 13 | Truncated tesseract (tat) |  | t{4,3,3} | (3) (3.8.8) | (1) (3.3.3) | 24 | 88 | 128 | 64 | |||
| 14 | Cantellated tesseract Small rhombated tesseract (srit) |  | rr{4,3,3} | (2) (3.4.4.4) | (2) (3.4.4) | (1) (3.3.3.3) | 56 | 248 | 288 | 96 | ||
| 15 | Runcinated tesseract (also runcinated 16-cell) Small disprismatotesseractihexadecachoron (sidpith) |  | t0,3{4,3,3} | (1) (4.4.4) | (3) (4.4.4) | (3) (3.4.4) | (1) (3.3.3) | 80 | 208 | 192 | 64 | |
| 16 | Bitruncated tesseract (also bitruncated 16-cell) Tesseractihexadecachoron (tah) | 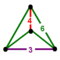 | 2t{4,3,3} | (2) (4.6.6) | (2) (3.6.6) | 24 | 120 | 192 | 96 | |||
| 18 | Cantitruncated tesseract Great rhombated tesseract (grit) |  | tr{4,3,3} | (2) (4.6.8) | (1) (3.4.4) | (1) (3.6.6) | 56 | 248 | 384 | 192 | ||
| 19 | Runcitruncated tesseract Prismatorhombated hexadecachoron (proh) | t0,1,3{4,3,3} | (1) (3.8.8) | (2) (4.4.8) | (1) (3.4.4) | (1) (3.4.3.4) | 80 | 368 | 480 | 192 | ||
| 21 | Omnitruncated tesseract (also omnitruncated 16-cell) Great disprismatotesseractihexadecachoron (gidpith) | 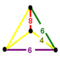 | t0,1,2,3{3,3,4} | (1) (4.6.8) | (1) (4.4.8) | (1) (4.4.6) | (1) (4.6.6) | 80 | 464 | 768 | 384 | |
| # | Name (Bowers style acronym) | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3 (8) | Pos. 2 (24) | Pos. 1 (32) | Pos. 0 (16) | Alt | Cells | Faces | Edges | Vertices | ||||
| [12] | Half tesseract Demitesseract = 16-cell (hex) |  | h{4,3,3}={3,3,4} | (4) (3.3.3) | (4) (3.3.3) | 16 | 32 | 24 | 8 | |||
| [17] | Cantic tesseract = Truncated 16-cell (thex) | 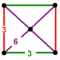 | h2{4,3,3}=t{4,3,3} | (4) (6.6.3) | (1) (3.3.3.3) | 24 | 96 | 120 | 48 | |||
| [11] | Runcic tesseract = Rectified tesseract (rit) | 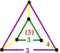 | h3{4,3,3}=r{4,3,3} | (3) (3.4.3.4) | (2) (3.3.3) | 24 | 88 | 96 | 32 | |||
| [16] | Runcicantic tesseract = Bitruncated tesseract (tah) | 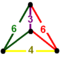 | h2,3{4,3,3}=2t{4,3,3} | (2) (3.4.3.4) | (2) (3.6.6) | 24 | 120 | 192 | 96 | |||
| [11] | = Rectified tesseract (rat) |  | h1{4,3,3}=r{4,3,3} | 24 | 88 | 96 | 32 | |||||
| [16] | = Bitruncated tesseract (tah) |  | h1,2{4,3,3}=2t{4,3,3} | 24 | 120 | 192 | 96 | |||||
| [23] | = Rectified 24-cell (rico) |  | h1,3{4,3,3}=rr{3,3,4} | 48 | 240 | 288 | 96 | |||||
| [24] | = Truncated 24-cell (tico) |  | h1,2,3{4,3,3}=tr{3,3,4} | 48 | 240 | 384 | 192 | |||||
| # | Name (Bowers style acronym) | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3 (8) | Pos. 2 (24) | Pos. 1 (32) | Pos. 0 (16) | Alt | Cells | Faces | Edges | Vertices | ||||
| Nonuniform | omnisnub tesseract Snub tesseract (snet)[20] (Or omnisnub 16-cell) | 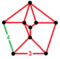 | ht0,1,2,3{4,3,3} | (1) (3.3.3.3.4) | (1) (3.3.3.4) | (1) (3.3.3.3) | (1) (3.3.3.3.3) | (4) (3.3.3) | 272 | 944 | 864 | 192 |
16-cell truncations
[edit]| # | Name (Bowers name and acronym) | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3 (8) | Pos. 2 (24) | Pos. 1 (32) | Pos. 0 (16) | Alt | Cells | Faces | Edges | Vertices | ||||
| 12 | 16-cell Hexadecachoron[10] (hex) |  | {3,3,4} | (8) (3.3.3) | 16 | 32 | 24 | 8 | ||||
| [22] | *Rectified 16-cell (Same as 24-cell) (ico) | 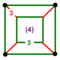 | r{3,3,4} | (2) (3.3.3.3) | (4) (3.3.3.3) | 24 | 96 | 96 | 24 | |||
| 17 | Truncated 16-cell Truncated hexadecachoron (thex) |  | t{3,3,4} | (1) (3.3.3.3) | (4) (3.6.6) | 24 | 96 | 120 | 48 | |||
| [23] | *Cantellated 16-cell (Same as rectified 24-cell) (rico) |  | rr{3,3,4} | (1) (3.4.3.4) | (2) (4.4.4) | (2) (3.4.3.4) | 48 | 240 | 288 | 96 | ||
| [15] | Runcinated 16-cell (also runcinated tesseract) (sidpith) |  | t0,3{3,3,4} | (1) (4.4.4) | (3) (4.4.4) | (3) (3.4.4) | (1) (3.3.3) | 80 | 208 | 192 | 64 | |
| [16] | Bitruncated 16-cell (also bitruncated tesseract) (tah) |  | 2t{3,3,4} | (2) (4.6.6) | (2) (3.6.6) | 24 | 120 | 192 | 96 | |||
| [24] | *Cantitruncated 16-cell (Same as truncated 24-cell) (tico) | 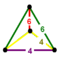 | tr{3,3,4} | (1) (4.6.6) | (1) (4.4.4) | (2) (4.6.6) | 48 | 240 | 384 | 192 | ||
| 20 | Runcitruncated 16-cell Prismatorhombated tesseract (prit) | t0,1,3{3,3,4} | (1) (3.4.4.4) | (1) (4.4.4) | (2) (4.4.6) | (1) (3.6.6) | 80 | 368 | 480 | 192 | ||
| [21] | Omnitruncated 16-cell (also omnitruncated tesseract) (gidpith) |  | t0,1,2,3{3,3,4} | (1) (4.6.8) | (1) (4.4.8) | (1) (4.4.6) | (1) (4.6.6) | 80 | 464 | 768 | 384 | |
| [31] | alternated cantitruncated 16-cell (Same as the snub 24-cell) (sadi) |  | sr{3,3,4} | (1) (3.3.3.3.3) | (1) (3.3.3) | (2) (3.3.3.3.3) | (4) (3.3.3) | 144 | 480 | 432 | 96 | |
| Nonuniform | Runcic snub rectified 16-cell Pyritosnub tesseract (pysnet) |  | sr3{3,3,4} | (1) (3.4.4.4) | (2) (3.4.4) | (1) (4.4.4) | (1) (3.3.3.3.3) | (2) (3.4.4) | 176 | 656 | 672 | 192 |
- (*) Just as rectifying the tetrahedron produces the octahedron, rectifying the 16-cell produces the 24-cell, the regular member of the following family.
The snub 24-cell is repeat to this family for completeness. It is an alternation of the cantitruncated 16-cell or truncated 24-cell, with the half symmetry group [(3,3)+,4]. The truncated octahedral cells become icosahedra. The cubes becomes tetrahedra, and 96 new tetrahedra are created in the gaps from the removed vertices.
The F4 family
[edit]This family has diploid icositetrachoric symmetry,[10] [3,4,3], of order 24×48=1152: the 48 symmetries of the octahedron for each of the 24 cells. There are 3 small index subgroups, with the first two isomorphic pairs generating uniform 4-polytopes which are also repeated in other families, [3+,4,3], [3,4,3+], and [3,4,3]+, all order 576.
| # | Name | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3 (24) | Pos. 2 (96) | Pos. 1 (96) | Pos. 0 (24) | Cells | Faces | Edges | Vertices | ||||
| 22 | 24-cell (Same as rectified 16-cell) Icositetrachoron[10] (ico) |  | {3,4,3} | (6) (3.3.3.3) | 24 | 96 | 96 | 24 | |||
| 23 | rectified 24-cell (Same as cantellated 16-cell) Rectified icositetrachoron (rico) |  | r{3,4,3} | (3) (3.4.3.4) | (2) (4.4.4) | 48 | 240 | 288 | 96 | ||
| 24 | truncated 24-cell (Same as cantitruncated 16-cell) Truncated icositetrachoron (tico) | 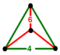 | t{3,4,3} | (3) (4.6.6) | (1) (4.4.4) | 48 | 240 | 384 | 192 | ||
| 25 | cantellated 24-cell Small rhombated icositetrachoron (srico) |  | rr{3,4,3} | (2) (3.4.4.4) | (2) (3.4.4) | (1) (3.4.3.4) | 144 | 720 | 864 | 288 | |
| 28 | cantitruncated 24-cell Great rhombated icositetrachoron (grico) |  | tr{3,4,3} | (2) (4.6.8) | (1) (3.4.4) | (1) (3.8.8) | 144 | 720 | 1152 | 576 | |
| 29 | runcitruncated 24-cell Prismatorhombated icositetrachoron (prico) | t0,1,3{3,4,3} | (1) (4.6.6) | (2) (4.4.6) | (1) (3.4.4) | (1) (3.4.4.4) | 240 | 1104 | 1440 | 576 | |
| # | Name | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3 (24) | Pos. 2 (96) | Pos. 1 (96) | Pos. 0 (24) | Alt | Cells | Faces | Edges | Vertices | ||||
| 31 | †snub 24-cell Snub disicositetrachoron (sadi) |  | s{3,4,3} | (3) (3.3.3.3.3) | (1) (3.3.3) | (4) (3.3.3) | 144 | 480 | 432 | 96 | ||
| Nonuniform | runcic snub 24-cell Prismatorhombisnub icositetrachoron (prissi) | 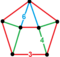 | s3{3,4,3} | (1) (3.3.3.3.3) | (2) (3.4.4) | (1) (3.6.6) | (3) Tricup | 240 | 960 | 1008 | 288 | |
| [25] | cantic snub 24-cell (Same as cantellated 24-cell) (srico) | 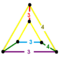 | s2{3,4,3} | (2) (3.4.4.4) | (1) (3.4.3.4) | (2) (3.4.4) | 144 | 720 | 864 | 288 | ||
| [29] | runcicantic snub 24-cell (Same as runcitruncated 24-cell) (prico) | s2,3{3,4,3} | (1) (4.6.6) | (1) (3.4.4) | (1) (3.4.4.4) | (2) (4.4.6) | 240 | 1104 | 1440 | 576 | ||
- (†) The snub 24-cell here, despite its common name, is not analogous to the snub cube; rather, it is derived by an alternation of the truncated 24-cell. Its symmetry number is only 576, (the ionic diminished icositetrachoric group, [3+,4,3]).
Like the 5-cell, the 24-cell is self-dual, and so the following three forms have twice as many symmetries, bringing their total to 2304 (extended icositetrachoric symmetry [[3,4,3]]).
| # | Name | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|
| Pos. 3-0 (48) | Pos. 2-1 (192) | Cells | Faces | Edges | Vertices | ||||
| 26 | runcinated 24-cell Small prismatotetracontoctachoron (spic) |  | t0,3{3,4,3} | (2) (3.3.3.3) | (6) (3.4.4) | 240 | 672 | 576 | 144 |
| 27 | bitruncated 24-cell Tetracontoctachoron (cont) |  | 2t{3,4,3} | (4) (3.8.8) | 48 | 336 | 576 | 288 | |
| 30 | omnitruncated 24-cell Great prismatotetracontoctachoron (gippic) |  | t0,1,2,3{3,4,3} | (2) (4.6.8) | (2) (4.4.6) | 240 | 1392 | 2304 | 1152 |
| # | Name | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3-0 (48) | Pos. 2-1 (192) | Alt | Cells | Faces | Edges | Vertices | ||||
| Nonuniform | omnisnub 24-cell Snub tetracontoctachoron (snoc) Snub icositetrachoron (sni)[21] | 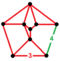 | ht0,1,2,3{3,4,3} | (2) (3.3.3.3.4) | (2) (3.3.3.3) | (4) (3.3.3) | 816 | 2832 | 2592 | 576 |
The H4 family
[edit]This family has diploid hexacosichoric symmetry,[10] [5,3,3], of order 120×120=24×600=14400: 120 for each of the 120 dodecahedra, or 24 for each of the 600 tetrahedra. There is one small index subgroups [5,3,3]+, all order 7200.
120-cell truncations
[edit]| # | Name (Bowers name and acronym) | Vertex figure | Coxeter diagram and Schläfli symbols | Cell counts by location | Element counts | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3 (120) | Pos. 2 (720) | Pos. 1 (1200) | Pos. 0 (600) | Alt | Cells | Faces | Edges | Vertices | ||||
| 32 | 120-cell (hecatonicosachoron or dodecacontachoron)[10] Hecatonicosachoron (hi) |  | {5,3,3} | (4) (5.5.5) | 120 | 720 | 1200 | 600 | ||||
| 33 | rectified 120-cell Rectified hecatonicosachoron (rahi) |  | r{5,3,3} | (3) (3.5.3.5) | (2) (3.3.3) | 720 | 3120 | 3600 | 1200 | |||
| 36 | truncated 120-cell Truncated hecatonicosachoron (thi) | 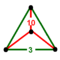 | t{5,3,3} | (3) (3.10.10) | (1) (3.3.3) | 720 | 3120 | 4800 | 2400 | |||
| 37 | cantellated 120-cell Small rhombated hecatonicosachoron (srahi) |  | rr{5,3,3} | (2) (3.4.5.4) | (2) (3.4.4) | (1) (3.3.3.3) | 1920 | 9120 | 10800 | 3600 | ||
| 38 | runcinated 120-cell (also runcinated 600-cell) Small disprismatohexacosihecatonicosachoron (sidpixhi) |  | t0,3{5,3,3} | (1) (5.5.5) | (3) (4.4.5) | (3) (3.4.4) | (1) (3.3.3) | 2640 | 7440 | 7200 | 2400 | |
| 39 | bitruncated 120-cell (also bitruncated 600-cell) Hexacosihecatonicosachoron (xhi) |  | 2t{5,3,3} | (2) (5.6.6) | (2) (3.6.6) | 720 | 4320 | 7200 | 3600 | |||
| 42 | cantitruncated 120-cell Great rhombated hecatonicosachoron (grahi) |  | tr{5,3,3} | (2) (4.6.10) | (1) (3.4.4) | (1) (3.6.6) | 1920 | 9120 | 14400 | 7200 | ||
| 43 | runcitruncated 120-cell Prismatorhombated hexacosichoron (prix) | t0,1,3{5,3,3} | (1) (3.10.10) | (2) (4.4.10) | (1) (3.4.4) | (1) (3.4.3.4) | 2640 | 13440 | 18000 | 7200 | ||
| 46 | omnitruncated 120-cell (also omnitruncated 600-cell) Great disprismatohexacosihecatonicosachoron (gidpixhi) |  | t0,1,2,3{5,3,3} | (1) (4.6.10) | (1) (4.4.10) | (1) (4.4.6) | (1) (4.6.6) | 2640 | 17040 | 28800 | 14400 | |
| Nonuniform | omnisnub 120-cell Snub hecatonicosachoron (snixhi)[22] (Same as the omnisnub 600-cell) |  | ht0,1,2,3{5,3,3} | (3.3.3.3.5) | (3.3.3.5) | (3.3.3.3) | (3.3.3.3.3) | (3.3.3) | 9840 | 35040 | 32400 | 7200 |
600-cell truncations
[edit]| # | Name (Bowers style acronym) | Vertex figure | Coxeter diagram and Schläfli symbols | Symmetry | Cell counts by location | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 3 (120) | Pos. 2 (720) | Pos. 1 (1200) | Pos. 0 (600) | Cells | Faces | Edges | Vertices | |||||
| 35 | 600-cell Hexacosichoron[10] (ex) |  | {3,3,5} | [5,3,3] order 14400 | (20) (3.3.3) | 600 | 1200 | 720 | 120 | |||
| [47] | 20-diminished 600-cell = Grand antiprism (gap) | 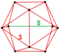 | Nonwythoffian construction | [[10,2+,10]] order 400 Index 36 | (2) (3.3.3.5) | (12) (3.3.3) | 320 | 720 | 500 | 100 | ||
| [31] | 24-diminished 600-cell = Snub 24-cell (sadi) |  | Nonwythoffian construction | [3+,4,3] order 576 index 25 | (3) (3.3.3.3.3) | (5) (3.3.3) | 144 | 480 | 432 | 96 | ||
| Nonuniform | bi-24-diminished 600-cell Bi-icositetradiminished hexacosichoron (bidex) | Nonwythoffian construction | order 144 index 100 | (6) tdi | 48 | 192 | 216 | 72 | ||||
| 34 | rectified 600-cell Rectified hexacosichoron (rox) | 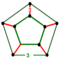 | r{3,3,5} | [5,3,3] | (2) (3.3.3.3.3) | (5) (3.3.3.3) | 720 | 3600 | 3600 | 720 | ||
| Nonuniform | 120-diminished rectified 600-cell Swirlprismatodiminished rectified hexacosichoron (spidrox) |  | Nonwythoffian construction | order 1200 index 12 | (2) 3.3.3.5 | (2) 4.4.5 | (5) P4 | 840 | 2640 | 2400 | 600 | |
| 41 | truncated 600-cell Truncated hexacosichoron (tex) |  | t{3,3,5} | [5,3,3] | (1) (3.3.3.3.3) | (5) (3.6.6) | 720 | 3600 | 4320 | 1440 | ||
| 40 | cantellated 600-cell Small rhombated hexacosichoron (srix) |  | rr{3,3,5} | [5,3,3] | (1) (3.5.3.5) | (2) (4.4.5) | (1) (3.4.3.4) | 1440 | 8640 | 10800 | 3600 | |
| [38] | runcinated 600-cell (also runcinated 120-cell) (sidpixhi) |  | t0,3{3,3,5} | [5,3,3] | (1) (5.5.5) | (3) (4.4.5) | (3) (3.4.4) | (1) (3.3.3) | 2640 | 7440 | 7200 | 2400 |
| [39] | bitruncated 600-cell (also bitruncated 120-cell) (xhi) |  | 2t{3,3,5} | [5,3,3] | (2) (5.6.6) | (2) (3.6.6) | 720 | 4320 | 7200 | 3600 | ||
| 45 | cantitruncated 600-cell Great rhombated hexacosichoron (grix) |  | tr{3,3,5} | [5,3,3] | (1) (5.6.6) | (1) (4.4.5) | (2) (4.6.6) | 1440 | 8640 | 14400 | 7200 | |
| 44 | runcitruncated 600-cell Prismatorhombated hecatonicosachoron (prahi) | t0,1,3{3,3,5} | [5,3,3] | (1) (3.4.5.4) | (1) (4.4.5) | (2) (4.4.6) | (1) (3.6.6) | 2640 | 13440 | 18000 | 7200 | |
| [46] | omnitruncated 600-cell (also omnitruncated 120-cell) (gidpixhi) |  | t0,1,2,3{3,3,5} | [5,3,3] | (1) (4.6.10) | (1) (4.4.10) | (1) (4.4.6) | (1) (4.6.6) | 2640 | 17040 | 28800 | 14400 |
The D4 family
[edit]This demitesseract family, [31,1,1], introduces no new uniform 4-polytopes, but it is worthy to repeat these alternative constructions. This family has order 12×16=192: 4!/2=12 permutations of the four axes, half as alternated, 24=16 for reflection in each axis. There is one small index subgroups that generating uniform 4-polytopes, [31,1,1]+, order 96.
| # | Name (Bowers style acronym) | Vertex figure | Coxeter diagram | Cell counts by location | Element counts | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 0 (8) | Pos. 2 (24) | Pos. 1 (8) | Pos. 3 (8) | Pos. Alt (96) | 3 | 2 | 1 | 0 | ||||
| [12] | demitesseract half tesseract (Same as 16-cell) (hex) |  | ||||||||||


 French
French Deutsch
Deutsch