Sphere packing in a sphere
Sphere packing in a sphere is a three-dimensional packing problem with the objective of packing a given number of equal spheres inside a unit sphere. It is the three-dimensional equivalent of the circle packing in a circle problem in two dimensions.
| Number of inner spheres | Maximum radius of inner spheres[1] | Packing density | Optimality | Arrangement | Diagram | |
|---|---|---|---|---|---|---|
| Exact form | Approximate | |||||
| 1 | 1.0000 | 1 | Trivially optimal. | Point |  | |
| 2 | 0.5000 | 0.25 | Trivially optimal. | Line segment | 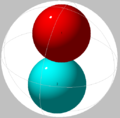 | |
| 3 | 0.4641... | 0.29988... | Trivially optimal. | Triangle |  | |
| 4 | 0.4494... | 0.36326... | Proven optimal. | Tetrahedron |  | |
| 5 | 0.4142... | 0.35533... | Proven optimal. | Trigonal bipyramid |  | |
| 6 | 0.4142... | 0.42640... | Proven optimal. | Octahedron |  | |
| 7 | 0.3859... | 0.40231... | Proven optimal. | Capped octahedron |  | |
| 8 | 0.3780... | 0.43217... | Proven optimal. | Square antiprism |  | |
| 9 | 0.3660... | 0.44134... | Proven optimal. | Tricapped trigonal prism |  | |
| 10 | 0.3530... | 0.44005... | Proven optimal. |  | ||
| 11 | 0.3445... | 0.45003... | Proven optimal. | Diminished icosahedron |  | |
| 12 | 0.3445... | 0.49095... | Proven optimal. | Icosahedron |  | |


 French
French Deutsch
Deutsch







