الگوریتم کلونی مورچگان - ویکی‌پدیا، دانشنامهٔ آزاد

همان‌طور که می‌دانیم مسئله یافتن کوتاهترین مسیر، یک مسئله بهینه سازیست که گاه حل آن بسیار دشوار است و گاه نیز بسیار زمانبر. برای مثال مسئله فروشنده دوره گرد را نیز می‌توان مطرح کرد. در این روش(ACo)، مورچه‌های مصنوعی به‌وسیلهٔ حرکت بر روی نمودار مسئله و با باقی گذاشتن نشانه‌هایی بر روی نمودار، همچون مورچه‌های واقعی که در مسیر حرکت خود نشانه‌های باقی می‌گذارند، باعث می‌شوند که مورچه‌های مصنوعی بعدی بتوانند راه‌حل‌های بهتری را برای مسئله فراهم نمایند. همچنین در این روش می‌توان توسط مسائل محاسباتی-عددی بر مبنای علم احتمالات بهترین مسیر را در یک نمودار یافت.

روش که از رفتار مورچه‌ها در یافتن مسیر بین محل لانه و غذا الهام گرفته شده؛ اولین بار در ۱۹۹۲ توسط مارکو دوریگو (Marco Dorigo) در پایان نامهٔ دکترایش مطرح شد...

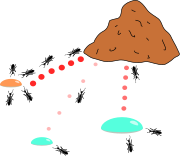
الگوریتم کلونی مورچه الهام گرفته شده از مطالعات و مشاهدات روی کلونی مورچه هاست. این مطالعات نشان داده که مورچه‌ها حشراتی اجتماعی هستند که در کلونی‌ها زندگی می‌کنند و رفتار آن‌ها بیشتر در جهت بقاء کلونی است تا در جهت بقاء یک جزء از آن. یکی از مهم‌ترین و جالبترین رفتار مورچه‌ها، رفتار آن‌ها برای یافتن غذا است و به ویژه چگونگی پیدا کردن کوتاهترین مسیر میان منابع غذایی و آشیانه. این نوع رفتار مورچه‌ها دارای نوعی هوشمندی توده‌ای است که اخیراً مورد توجه دانشمندان قرار گرفته‌است در دنیای واقعی مورچه‌ها ابتدا به‌طور تصادفی به این سو و آن سو می‌روند تا غذا بیابند. سپس به لانه بر می‌گردند و ردّی از فرومون (Pheromone) به جا می‌گذارند. چنین ردهایی پس از باران به رنگ سفید در می‌آیند و قابل رویت اند. مورچه‌های دیگر وقتی این مسیر را می‌یابند، گاه پرسه زدن را رها کرده و آن را دنبال می‌کنند. سپس اگر به غذا برسند به خانه بر می‌گردند و رد دیگری از خود در کنار رد قبل می‌گذارند؛ و به عبارتی مسیر قبل را تقویت می‌کنند. فرومون به مرور تبخیر می‌شود که از سه جهت مفید است:

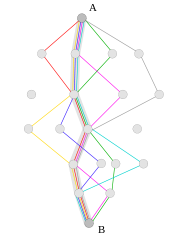
• باعث می‌شود مسیر جذابیت کمتری برای مورچه‌های بعدی داشته باشد. از آنجا که یک مورچه در زمان دراز راه‌های کوتاه‌تر را بیش تر می‌پیماید و تقویت می‌کند هر راهی بین خانه و غذا که کوتاه‌تر (بهتر) باشد بیشتر تقویت می‌شود و آنکه دورتر است کمتر.
• اگر فرومون اصلاً تبخیر نمی‌شد، مسیرهایی که چند بار طی می‌شدند، چنان بیش از حد جذّاب می‌شدند که جستجوی تصادفی برای غذا را بسیار محدود می‌کردند.
• وقتی غذای انتهای یک مسیر جذاب تمام می‌شد رد باقی می‌ماند.

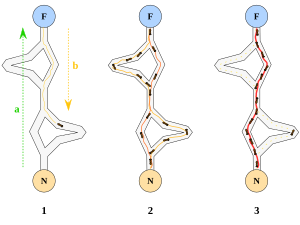
لذا وقتی یک مورچه مسیر کوتاهی (خوبی) را از خانه تا غذا بیابد بقیهٔ مورچه‌ها به احتمال زیادی همان مسیر را دنبال می‌کنند و با تقویت مداوم آن مسیر و تبخیر ردهای دیگر، به مرور همهٔ مورچه‌ها هم مسیر می‌شوند. هدف الگوریتم مورچه‌ها تقلید این رفتار توسط مورچه‌هایی مصنوعی ست که روی نمودار در حال حرکت اند. مسئله یافتن کوتاه‌ترین مسیر است و حلالش این مورچه‌های مصنوعی اند.

از کابردهای این الگوریتم، رسیدن به راه حل تقریباً بهینه در مسئله فروشنده دوره‌گرد است. به طوری که انواع الگوریتم مورچه‌ها برای حل این مسئله تهیه شده. زیرا این روش عددی نسبت به روشهای تحلیلی و genetic در مواردی که نمودار مدام با زمان تغییر کند یک مزیت دارد؛ و آن این که الگوریتمی ست با قابلیت تکرار؛ و لذا با گذر زمان می‌تواند جواب را به‌طور زنده تغییر دهد؛ که این خاصیت در روتینگ شبکه‌های کامپیوتری و سامانه حمل و نقل شهری مهم است.
در مسئله فروشنده دوره گرد باید از یک شهر شروع کرده، به شهرهای دیگر برود و سپس به شهر مبدأ بازگردد بطوریکه از هر شهر فقط یکبار عبور کند و کوتاهترین مسیر را نیز طی کرده باشد. اگر تعداد این شهرها n باشد در حالت کلی این مسئله از مرتبه (n-1)! است که برای فقط ۲۱ شهر زمان واقعاً زیادی می‌برد:

روز۱۰۱۳*۷/۱ = S۱۰۱۶*۴۳۳/۲ = ms۱۰*۱۰۱۸*۴۳۳/۲ =!۲۰

با انجام یک الگوریتم برنامه سازی پویا برای این مسئله، زمان از مرتبه نمایی به دست می‌آید که آن هم مناسب نیست. البته الگوریتم‌های دیگری نیز ارائه شده ولی هیچ‌کدام کارایی مناسبی ندارند. ACO الگوریتم کامل و مناسبی برای حل مسئله TSP است.

<تبخیر شدن فرومون> و <احتمال-تصادف>به مورچه‌ها امکان پیدا کردن کوتاهترین مسیر را می‌دهد. این دو ویژگی باعث ایجاد انعطاف در حل هرگونه مسئله بهینه‌سازی می‌شوند. مثلاً در گراف شهرهای مسئله فروشنده دوره گرد، اگر یکی از یالها (یا گره‌ها) حذف شود الگوریتم این توانایی را دارد تا به سرعت مسیر بهینه را با توجه به شرایط جدید پیدا کند. به این ترتیب که اگر یال (یا گره‌ای) حذف شود دیگر لازم نیست که الگوریتم از ابتدا مسئله را حل کند بلکه از جایی که مسئله حل شده تا محل حذف یال (یا گره) هنوز بهترین مسیر را داریم، از این به بعد مورچه‌ها می‌توانند پس از مدت کوتاهی مسیر بهینه (کوتاهترین) را بیابند.

از کاربردهای ACO می‌توان به بهینه کردن هر مسئله‌ای که نیاز به یافتن کوتاهترین مسیر دارد، اشاره نمود:

۱. مسیر یابی داخل شهری و بین شهری.

۲. مسیر یابی بین پست‌های شبکه‌های توزیع برق ولتاژ بالا.

۳. مسیر یابی شبکه‌های کامپیوتری.

۴. استفاده از وب.

۵. استفاده ازACOدربهینه سازی شبکه‌های توزیع آب

۶. لبه یابی تصاویر

پروسهٔ پیدا کردن کوتاه‌ترین مسیر توسط مورچه‌ها، ویژگی‌های بسیار جالبی دارد، اول از همه قابلیت تعمیم زیاد و خود- سازمانده بودن آن است. در ضمن هیچ مکانیزم کنترل مرکزی ای وجود ندارد. ویژگی دوم قدرت زیاد آن است. سیستم شامل تعداد زیادی از عواملی است که به تنهایی بی‌اهمیت هستند بنابراین حتی تلفات یک عامل مهم، تأثیر زیادی روی کارایی سیستم ندارد. سومین ویژگی این است که، پروسه یک فرایند تطبیقی است. از آنجا که رفتار هیچ‌کدام از مورچه‌ها معین نیست و تعدادی از مورچه‌ها همچنان مسیر طولانی‌تر را انتخاب می‌کنند، سیستم می‌تواند خود را با تغییرات محیط منطبق کند و ویژگی آخر اینکه این پروسه قابل توسعه است و می‌تواند به اندازهٔ دلخواه بزرگ شود. همین ویژگی‌ها الهام بخش طراحی الگوریتم‌هایی شده‌اند که در مسائلی که نیازمند این ویژگی‌ها هستند کاربرد دارند. اولین الگوریتمی که بر این اساس معرفی شد، الگوریتم ABC بود. چند نمونه دیگر از این الگوریتم‌ها عبارتند از: AntNet,ARA,PERA,AntHocNet.

در پایین تعدادی از انواع شناخته شده از الگوریتم بهینه‌سازی مورچگان را معرفی می‌کنیم:

۱- سیستم مورچه نخبگان: در این روش بهترین راه حل کلی در هر تکرار فرمون آزاد می‌کند. همچنین این روش برای تمام مورچه‌های مصنوعی باید انجام شود.

۲- سیستم مورچه ماکسیموم – مینیمم: یک مقدار کمینه و بیشینه برای فرمون تعیین کرده و فقط در هر مرحله بهترین جواب این مقدار را آزاد می‌کند و تمام گره‌های مجاور ان به مقدار فرمون بیشینه مقدار دهی اولیه می‌شوند.

۳- سیستم کلونی مورچه: که در بالا توضیحات کافی داده شده‌است.

۴- سیستم مورچه بر اساس رتبه: تمام راه حل‌های بدست آماده بر اساس طول جواب رتبه‌بندی می‌شوند و بر اساس همین رتبه‌بندی مقدار فرمون آزاد سازی شده توسط آن‌ها مشخص خواهد شد و راه حل با طول کمتر از راه حل دیگر با طول بیشتر مقدار فرمون بیشتری آزاد می‌کند.

۵ - سیستم مورچه متعامد مداوم: در این روش مکانیزم تولید فرمون به مورچه اجازه می‌دهد تا برای رسیدن به جواب بهتر و مشترک با بقیه مورچه‌ها جستجو انجام دهد با استفاده از روش طراحی متعامد مورچه می‌تواند در دامنه تعریف شده خود به صورت مداوم برای بدست آوردن بهترین جواب جستجو کند که این عمل به هدف رسیدن به جواب بهینه و صحیح ما را نزدیک می‌کند. روش طراحی متعامد می‌تواند به دیگر روش‌های جستجو دیگر گسترش پیدا کنند تا به مزیت‌های این روش‌های جستجو اضافه کند.

کورش عشقی؛ مهدی کریمی نسب؛ تحلیل الگوریتمها و طراحی روشهای فرابتکاری؛ انتشارات دانشگاه شریف؛ ۱۳۹۵

• نسخه فرانسوی مقاله
• نسخه انگلیسی مقاله
• Frederick Ducatelle, Adaptive Routing in Ad Hoc Wireless Multi-hop Networks, Universita della Svizzera italiana, Lugano, Switzerland, 2007.