e (عدد) - ویکیپدیا، دانشنامهٔ آزاد

| بخشی از مجموعه مقالههای پیرامون: |
| ثابت ریاضی e |
|---|
 |
| لگاریتم طبیعی • تابع نمایی |
| کاربردها |
| فرمول اویلر • نیمهعمر • رشد نمایی • ثابت واپاشی • تساوی اویلر |
| تعریف e: |
| اثبات گنگ بودن عدد e • نمایش عدد e • نظریه لیندمن-وایرشتراس |
| افراد |
| جان نپر • لئونارد اویلر |
عدد که به عدد اویلر هم معروف است، ثابت ریاضیاتی است که تقریباً برابر بوده و میتوان آن را به طرق متعددی بهدستآورد (مشخص نمود، مشخصهسازی کرد). این عدد پایهٔ لگاریتم طبیعی است.[۱][۲][۳] این عدد برابر با حد است وقتی به سمت بینهایت میل کند؛ عبارتی که در بحث بهره مرکب (و مباحث دیگر) نیز ظهور پیدا میکند. همچنین این عدد را میتوان به صورت جمع سری بینهایت زیر نیز محاسبه کرد:[۴][۵]
همچنین این عدد، عدد منحصربهفردی است که شیب نمودار تابع را در نقطه برابر ۱ میکند.[۶]
تابع نمایی ، تابع منحصربهفردی است با این خاصیت که برابر با مشتق خود بوده؛ به گونهای که مقدار اولیهٔ آن است (و لذا میتوان را به صورت تعریف کرد). لگاریتم طبیعی، یا لگاریتم در پایه ، وارون تابع نمایی طبیعی است. لگاریتم طبیعی عددی چون را میتوان بهطور مستقیم توسط ناحیه زیر نمودار بین و تعریف کرد. در این صورت برابر با مقداری از است که این مساحت را برابر ۱ میکند (تصویر را ببینید). از طرق متعدد دیگری نیز میتوان این عدد را مشخص کرد.
برخی مواقع به ، به یاد لئونارد اویلر، عدد اویلر (اشتباه نشود با ، ثابت اویلر-ماسکرونی، که برخی مواقع به آن ثابت اویلر نیز گفته میشود)، یا به یاد جان نپر، ثابت نپر (Napier's Constant) نیز گفته میشود.[۵] با این حال، حرف e را که اویلر برای نمایش این ثابت انتخاب کرد، به افتخارش نگه داشتند.[۷] این ثابت توسط ریاضیدان سوئیسی، یاکوب برنولی (یا جیکوب برنولی)، طی مطالعه بهره مرکب کشف شد.[۸][۹]
عدد ، در کنار ۰، ۱، و اهمیت قابل توجهی در ریاضیات دارد.[۱۰] تمام پنج عدد مذکور، نقشهای مهمی را در کل ریاضیات داشته و مکرر ظاهر میشوند. تمام این پنج عدد در یک فرمول، یعنی اتحاد اویلر ظاهر میگردند. عدد ، همچون یک عدد گنگ (یعنی نمیتوان آن را به صورت نسبتی از دو عدد صحیح نمایش داد) و متعالی (یعنی نمیتوان آن را به صورت ریشه ای از یک چندجملهای ناصفر با ضرایب گویا نوشت) است.[۵] عدد تا پنجاه رقم در مبنای ده به صورت زیر است:
تاریخچه
[ویرایش]اولین اشاره به این عدد، در جدولی که در ضمیمهٔ مقالهٔ مربوط به لگاریتم جان نپر در سال ۱۶۱۸ انتشار یافته بود مشاهده میشود.[۱۱] با این حال، این مقاله توضیحی راجع به این عدد نمیداد بلکه تنها لیستی از لگاریتمهای حساب شده در مبنای این عدد را نشان میداد. به نظر میرسد که این جدول توسط ویلیام اوترد تهیه شدهاست. اما «کشف» این عدد توسط ژاکوب برنولی به انجام رسید، کسی که تلاش میکرد مقدار عبارت زیر را محاسبه کند (که در حقیقت همان e است):
اولین استفاده شناخته شده از این عدد، که آن زمان با b نمایش داده میشد، در مکاتبات بین گوتفرید لایبنیتس و کریستیان هویگنس بین سالهای ۱۶۹۰ تا ۱۶۹۱ مشاهده شدهاست. همچنین برای اولین بار اویلر بین سالهای ۱۷۲۷ تا ۱۷۲۸ شروع به استفاده از e برای نمایش این عدد کرد[۱۲] و اولین استفاده از آن در مقاله، در مکانیک اویلر در سال ۱۷۳۶ مشاهده میشود. در حالی که سالهای پس از آن نیز عدهای از ریاضی دانان از c برای نمایش این عدد استفاده میکردند، اما e بیشتر مرسوم بود. در نهایت نیز e به عنوان نماد استاندارد این عدد امروزه استفاده میشود.
نماد e
[ویرایش]در اینکه چرا عدد ، با حرف e توسط اویلر نمایش داده شدهاست صحبتهای بسیاری است. برخی حرف اول کلمه exponential به معنای نمایی میدانند، برخی آن را ابتدای اسم اویلر (به آلمانی: Euler) میدانند. برخی نیز میگویند چون حروف c,b،a و d در ریاضیات تا آن زمان به کرات استفاده شده بود، اویلر حرف e را برای نمایش این عدد استفاده کرد. هر دلیلی داشت، به هر حال امروزه اغلب این عدد با نام اویلر میشناسند.
لازم است ذکر شود که اویلر علاقه زیادی به استفاده از نمادهای ریاضی داشت و ریاضیات امروز علاوه بر عدد در ارتباط با مواردی مانند در بحث اعداد مختلط، در بحث توابع و بسیاری دیگر نمادها مدیون ابداعات اویلر است.
کاربردها
[ویرایش]مسئله بهره مرکب
[ویرایش]برنولی هنگام مطالعه بر روی مسئله بهره مرکب توانست این عدد را کشف کند.
به عنوان مثال یک حساب را فرض کنید که در آن باشد و بهرهٔ آن در سال است. اگر بهره یک باره در پایان سال محاسبه و پرداخت شود، در پایان سال در حساب خواهیم داشت. اما اگر بهره دو بار در سال یعنی شش ماه یک بار به اندازهٔ محاسبه شود، مقدار حساب تا پایان سال دو بار در ۱٫۵ ضرب خواهد شد یعنی . اگر چهار بار این کار صورت گیرد، حساب در پایان سال برابر میشود و اگر ماهانه محاسبه شود .
برنولی متوجه شد که این سری برای محاسبه در بازههای زمانی کوچکتر و بیشتر به یک عدد ثابت نزدیک میشود. محاسبهٔ هفتگی سود منجر به بهدست آوردن در پایان سال میشود، در حالی که محاسبهٔ روزانه آن با ۲ سنت افزایش به عدد میرسد. با استفاده از n بازه برای محاسبهٔ سود در هر بازه، مشاهده میگردد که با افزایش n به سمت اعداد بزرگتر مقدار مانده در حساب در پایان سال به عدد e نزدیکتر میشود، بهطوری که اگر محاسبه و پرداخت سود به صورت پیوسته صورت گیرد به عدد خواهیم رسید. بهطور کلی تر، حسابی با و سود با محاسبهٔ پیوستهٔ سود در یک سال به عدد خواهد رسید.
آزمایش برنولی
[ویرایش]عدد e در نظریه احتمالات، جایی که به نظر نمیرسد بهطور واضح هیچ نرخ رشد نمایی وجود داشته باشد، نیز نقش بسزایی ایفا میکند. برای مثال فرض کنید که قمارباز در حال بازی با یک ماشین اسلات (به انگلیسی: slot machine) است. قمارباز یک از n شانس پیروزی دارد و این بازی را n بار انجام میدهد. داریم برای nهای بزرگ (برای مثال چندین میلیون بازی) احتمال این که قمارباز در تمام بازیها شکست بخورد برابر با است.
این یک مثال از آزمایش برنولی است. هر بار که یک قمارباز بازی میکند یک در میلیون شانس پیروزی دارد. یک میلیون بار بازی کردن را میتوان به وسیله توزیع دوجملهای مدلسازی کرد. پیروزی در k بار از این یک میلیون بار برابر است با:
در حالت خاصی که در آن k برابر صفر است، یعنی عدم پیروزی در تمامی بازیها، داریم:
این عدد بسیار به عدد نزدیک است و حد آن نیز به این عدد نزدیک خواهد شد:
مسئله پریش
[ویرایش]یکی دیگر از کاربردهای e توسط ژاکوب برنولی در کنار پیر ریموند دو مونتمورت (به فرانسوی: Pierre Raymond de Montmort) این بار هنگام کار کردن بر روی مسئله پریش که به اسم مسئله تحویل کلاه نیز شناخته میشود، کشف شد.[۱۳] فرض کنید n نفر به یک مهمانی دعوت شدهاند، هر نفر هنگام ورود کلاهش را به پیشخدمت میدهد و او نیز آنها را در n جعبه که هر کدام به نام یکی از مهمانها نامگذاری شدهاست، میگذارد. اما پیشخدمت هویت مهمانها را نمیداند پس او هر کلاه را به صورت تصادفی در یکی از جعبهها میگذارد. مسئله دو مونتمورت این است که احتمال اینکه هیچکدام از کلاهها داخل جعبهٔ خودشان قرار نگرفته باشند چقدر است. پاسخ اینگونهاست:
با زیاد شدن تعداد مهمانها و میل کردن n به سمت بینهایت مقدار به سمت میل خواهد کرد. به علاوه، تعداد حالاتی که کلاهها در جعبههای میتوانند قرار بگیرند بهطوری که هیچ کلاهی در سرجای خودش نباشد برابر است که باید به نزدیکترین عدد صحیح گرد شود.[۱۴]
مجانبها
[ویرایش]عدد e در بحث مجانبها و روند صعودی توابع نیز نقش خاصی بازی میکند. برای مثال این عدد همراه با عدد پی (به یونانی: π) در تقریب استرلینگ برای تابع فاکتوریل دیده میشود.[۱۵][۱۶][۱۷][۱۸][۱۹]
نتیجهٔ مستقیم این معادله به حد زیر برای به دست آوردن عدد e منجر میشود.
e در ریاضیات
[ویرایش]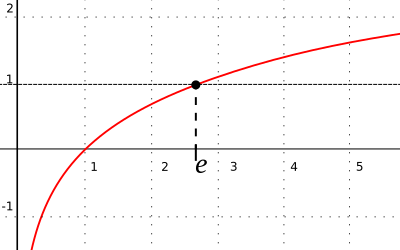
انگیزهٔ اصلی کشف عدد e، بهخصوص در ریاضیات، حل مشتقها و انتگرالها شامل توابع نمایی و لگاریتم بودهاست.[۲۰] مشتق تابع عمومی نمایی برابر است با حد عبارت زیر:
حد قسمت راست از متغیر x مستقل است و فقط به مقدار a مرتبط است. وقتی که پایهٔ تابع نمایی برابر e باشد، مقدار این حد برابر یک میشود. پس e را به صورت نمادین توسط عبارت زیر تعریف میکنند:
بنابراین تابع نمایی با پایهٔ e برای محاسبات حساب دیفرانسیل بسیار مناسب است. انتخاب e به جای اعداد دیگر، به عنوان پایهٔ تابع نمایی مشتق گرفتن از این تابع را سادهتر کردهاست.
انگیزهٔ دیگر برای کشف e انتخاب آن برای مبنای لگاریتم طبیعی بودهاست.[۲۱] مشتق تابع لگاریتم عمومی برابر است با حد عبارت زیر:
که در عبارت آخر تغییر متغیر را داریم. آخرین حد در این محاسبه باز هم از x مستقل است و تنها به a بستگی دارد. بهطوری که اگر a برابر e شود این حد نیز برابر با یک میشود. پس به صورت نمادین داریم:
لگاریتم در این مبنای خاص (یعنی e) را لگاریتم طبیعی مینامند و آن را با "ln" نمایش میدهند. این تابع هنگام مشتق گرفتن رفتار مناسبی دارد و حد موجود در مشتق این تابع یک میشود.
پس از طریق دو راه به نتیجهٔ a=e خواهیم رسید. یک راه از طریق برابر بودن مشتق تابع نمایی با خودش یعنی . راه دیگر از طریق برابری مشتق تابع لگاریتمی با . در هر مورد، ما برای سادگی محاسبات عدد e را انتخاب میکنیم، با این حال هر دو راه ما را به یک e خواهند رساند.
تعریفهای جایگزین
[ویرایش]
روشهای دیگری نیز برای تعریف e موجود است: یک از آنها حد یک دنباله در بینهایت، دیگری مجموع یک سری نامتناهی است. همچنین تعاریف مختلفی توسط انتگرال نیز برای این عدد موجود است. بعضی از این تعاریف شامل موارد زیر میشود:
۱. عدد e، یک عدد حقیقی مثبت یکتای است؛ بهطوری که:
۲. عدد e، یک عدد حقیقی مثبت یکتای است؛ بهطوری که:
تعاریف زیر را میتوان از تعاریف اصلی اثبات کرد.
۳. عدد e حد یک دنباله در بینهایت است:
به صورت مشابه داریم:
۴. عدد e مجموع یک سری نامتناهی است:
در اینجا !n به معنای n فاکتوریل است.
۵. عدد e، یک عدد حقیقی مثبت یکتای است؛ بهطوری که:
خواص
[ویرایش]ریاضیات
[ویرایش]تابع نمایی از این رو دارای اهمیت فراوان در ریاضیات است که مشتقش برابر خودش است.
همینطور برای انتگرال این تابع داریم:
توابع نمایی
[ویرایش]
ماکزیمم مطلق تابع
در نقطهٔ رخ میدهد. همچنین به صورت مشابه نقطهای است که در آن، تابع
که برای xهای مثبت تعریف شدهاست، مینیمم مطلق میشود.
به صورت کلیتر برای تابع
که برای xهای مثبت تعریف شدهاست، مینیمم مطلق در نقطهٔ رخ خواهد داد.
تتریشن یا هایپر-۴ (به انگلیسی: tetration) نامتناهی
بر اساس نظریه اویلر همگرا خواهد شد؛ اگر و فقط اگر باشد (یا بهطور تقریبی x بین ۰/۰۶۶ و ۱/۴۴۴۷ باشد).
نظریه اعداد
[ویرایش]عدد e یک عدد گنگ است. لئونارد اویلر این موضوع را به وسیلهٔ نامتناهی شدن بسط کسرهای متوالی ساده، نشان داد.[۲۲] به علاوه عدد e یک عدد متعالی است. این عدد، اولین عددی بود که با وجود این که با هدف ایجاد یک عدد متعالی ساخته نشده بود، متعالی بودنش اثبات شد (در مقایسه با عدد لیوویل). چارلز هرمیت این موضوع را در سال ۱۸۷۳ اثبات کرد.
اعداد مختلط
[ویرایش]تابع نمایی از طریق بسط تیلور به صورت زیر درخواهد آمد:
به این علت که این سری حاوی خاصیتهای مهمی برای تابع است، مخصوصاً هنگامی که x مختلط باشد، از آن برای در فضای اعداد مختلط بسیار استفاده میشود. از این بسط و بسط تیلور توابع سینوس و کسینوس میتوان معادله اویلر را بهدستآورد:
که برای تمامی xهای مختلط صحیح است، که در مورد خاص x = π برابر معادلهٔ مشخصهٔ اویلر میشود:
همچنین از آن میتوان جواب چندگانهٔ لگاریتم زیر را بهدستآورد:
به علاوه، از این معادلهٔ میتوان بسط را بهدستآورد:
که به معادله دی موآور معروف است.
معادلهٔ
نیز به (Cis(x معروف است.
معادلات دیفرانسیل
[ویرایش]تابع
پاسخ عمومی تمامی معادلات دیفرانسیل خطی به صورت زیر است:
بهطوری که با جایگذاری آن در معادله دیفرانسیل خواهیم داشت:
که ریشههای آن، sهایی است که پاسخهای عمومی معادلهٔ دیفرانسیل اصلی را میسازد.
نحوهٔ نمایش
[ویرایش]ارقام اعشار
[ویرایش]تعداد ارقام اعشار شناخته شدهٔ عدد e به صورت فزایندهای در طول سدههای اخیر رشد کردهاست. این رشد مدیون بهبود کارایی کامپیوترها و همچنین بهبود الگوریتمهای محاسبهٔ این ارقام بودهاست.[۲۳][۲۴]
| تاریخ | تعداد رقم اعشار | محاسبه شده به وسیلهٔ |
|---|---|---|
| ۱۷۴۸ | ۱۸ | لئونارد اویلر[۲۵] |
| ۱۸۵۳ | ۱۳۷ | ویلیام شانکس |
| ۱۸۷۱ | ۲۰۵ | ویلیام شانکس |
| ۱۸۸۴ | ۳۴۶ | ج. مارکوس بورمن |
| ۱۹۴۶ | ۸۰۸ | نامشخص |
| ۱۹۴۹ | ۲٬۰۱۰ | جان فون نیومن (توسط کامپیوتر انیاک) |
| ۱۹۶۱ | ۱۰۰٬۲۶۵ | دانیل شانکس و جان رنچ[۲۶] |
| ۱۹۷۸ | ۱۱۶٬۰۰۰ | استفان گری وزنیک توسط کامپیوتر (اپل ۲[۲۷]) |
| ۱۹۹۴ آوریل | ۱۰٬۰۰۰٬۰۰۰ | رابرت نمیرف و جری بنل[۲۸] |
| ۱۹۹۷ می | ۱۸٬۱۹۹٬۹۷۸ | پاتریک دمیشل |
| ۱۹۹۷ اوت | ۲۰٬۰۰۰٬۰۰۰ | بیرگر سیفرت |
| ۱۹۹۷ سپتامبر | ۵۰٬۰۰۰٬۸۱۷ | پاتریک دمیشل |
| ۱۹۹۹ فوریه | ۲۰۰٬۰۰۰٬۵۷۹ | سباستین ودنیسکی |
| ۱۹۹۹ اکتبر | ۸۶۹٬۸۹۴٬۱۰۱ | سباستین ودنیسکی |
| ۱۹۹۹ نوامبر | ۱٬۲۵۰٬۰۰۰٬۰۰۰ | خاویر گردون[۲۹] |
| ۲۰۰۰ ژوئیه | ۲٬۱۴۷٬۴۸۳٬۶۴۸ | خاویر گردون و شیگرو کندو[۳۰] |
| ۲۰۰۰ ژوئیه | ۳٬۲۲۱٬۲۲۵٬۴۷۲ | کولین مارتین و خاویر گردون[۳۱] |
| ۲۰۰۰ اوت | ۶٬۴۴۲٬۴۵۰٬۹۴۴ | خاویر گردون و شیگرو کندو |
| ۲۰۰۰ اوت | ۱۲٬۸۸۴٬۹۰۱٬۰۰۰ | خاویر گردون و شیگرو کندو |
| ۲۰۰۳ اوت | ۲۵٬۱۰۰٬۰۰۰٬۰۰۰ | خاویر گردون و شیگرو کندو[۳۲] |
| ۲۰۰۳ سپتامبر | ۵۰٬۱۰۰٬۰۰۰٬۰۰۰ | خاویر گردون و شیگرو کندو[۳۳] |
| ۲۰۰۷ آوریل | ۱۰۰٬۰۰۰٬۰۰۰٬۰۰۰ | شیگرو کندو و استیو پالیارو[۳۴] |
| ۲۰۰۹ می | ۲۰۰٬۰۰۰٬۰۰۰٬۰۰۰ | شیگرو کندو و استیو پالیارو[۳۴] |
| ۲۰۱۰ فوریه | ۵۰۰٬۰۰۰٬۰۰۰٬۰۰۰ | الکساندر جی. لی[۳۵] |
| ۲۰۱۰ ژوئیه | ۱٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰ | الکساندر جی. لی و شیگرو کندو[۳۶] |
| ۲۰۱۵ ژوئن | ۱٬۴۰۰٬۰۰۰٬۰۰۰٬۰۰۰ | الی هبرت[۳۷] |
| ۲۰۱۶ فوریه | ۱٬۵۰۰٬۰۰۰٬۰۰۰٬۰۰۰ | رون واتکینز[۳۷] |
| ۲۰۱۶ می | ۲٬۵۰۰٬۰۰۰٬۰۰۰٬۰۰۰ | «یو یو»[۳۷] |
| ۲۰۱۶ اوت | ۵٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰ | رون واتکینز[۳۷] |
| ۲۰۱۹ ژانویه | ۸٬۰۰۰٬۰۰۰٬۰۰۰٬۰۰۰ | جرالد هافمن[۳۷] |
| ۲۰۲۰ دسامبر | ۳۱٬۴۱۵٬۹۲۶٬۵۳۵٬۸۹۷ | دیوید کریستل[۳۸] |
جستارهای وابسته
[ویرایش]منابع
[ویرایش]- ↑ "Compendium of Mathematical Symbols". Math Vault (به انگلیسی). 2020-03-01. Retrieved 2020-08-10.
- ↑ Swokowski, Earl William (1979). Calculus with Analytic Geometry (illustrated ed.). Taylor & Francis. p. 370. ISBN 978-0-87150-268-1. Extract of page 370
- ↑ "e - Euler's number". www.mathsisfun.com. Retrieved 2020-08-10.
- ↑ Encyclopedic Dictionary of Mathematics 142.D
- ↑ ۵٫۰ ۵٫۱ ۵٫۲ Weisstein, Eric W. "e". mathworld.wolfram.com (به انگلیسی). Retrieved 2020-08-10.
- ↑ Marsden, Jerrold; Weinstein, Alan (1985). Calculus I (2nd ed.). Springer. p. 319. ISBN 0-387-90974-5.
- ↑ Sondow, Jonathan. "e". Wolfram Mathworld. Wolfram Research. Retrieved 10 May 2011.
- ↑ Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics (illustrated ed.). Sterling Publishing Company. p. 166. ISBN 978-1-4027-5796-9. Extract of page 166
- ↑ O'Connor, J J; Robertson, E F. "The number e". MacTutor History of Mathematics.
- ↑ Howard Whitley Eves (1969). An Introduction to the History of Mathematics. Holt, Rinehart & Winston. ISBN 978-0-03-029558-4.
- ↑ O'Connor, J.J. , and Roberson, E.F. ; The MacTutor History of Mathematics archive: "The number e»; University of St. Andrews Scotland (2001)
- ↑ Meditatio in experimenta explosione tormentorum nuper instituta.
- ↑ Grinstead, C.M. and Snell, J.L. Introduction to probability theory بایگانیشده در ۲۷ ژوئیه ۲۰۱۱ توسط Wayback Machine (published online under the GFDL), p. ۸۵.
- ↑ Knuth (۱۹۹۷) The Art of Computer Programming Volume I, Addison-Wesley, p. ۱۸۳.
- ↑ Havil, J. Gamma (۲۰۰۳)، Exploring Euler's Constant، Princeton, NJ: Princeton University Press، ص. ۸۶–۸۸
- ↑ Robbins, H. «A Remark of Stirling's Formula." Amer. Math. Monthly 62, 26-29, 1955.
- ↑ Stirling, J. «Methodus differentialis, sive tractatus de summation et interpolation serierum infinitarium." London, 1730. English translation by Holliday, J. «The Differential Method: A Treatise of the Summation and Interpolation of Infinite Series.» ۱۷۴۹.
- ↑ Whittaker, E. T. and Robinson, G. «Stirling's Approximation to the Factorial.» §۷۰ in «The Calculus of Observations: A Treatise on Numerical Mathematics», 4th ed. New York: Dover, pp. 138-140, 1967.
- ↑ Stirling's Approximation
- ↑ برای مثال نگاه کنید به: Kline, M. (۱۹۹۸) Calculus: An intuitive and physical approach, Dover, section 12.3 "The Derived Functions of Logarithmic Functions."
- ↑ This is the approach taken by Klein (1998).
- ↑ «How Euler Did It: Who proved e is Irrational?» (PDF). بایگانیشده (PDF) از روی نسخه اصلی در ۲۵ سپتامبر ۲۰۰۶. دریافتشده در ۲۵ سپتامبر ۲۰۰۶.
- ↑ Sebah, P. and Gourdon, X. ; The constant e and its computation
- ↑ Gourdon, X. ; Reported large computations with PiFast
- ↑ New Scientist 21st July 2007 p.40
- ↑ [۱] Statement from Daniel Shanks & John W Wrench — We have computed e on a 7090 to ۱۰۰٬۲۶۵D by the obvious program. On page 78 of their article "Calculation of Pi to ۱۰۰٬۰۰۰ Decimals" in the journal Mathematics of Computation, vol ۱۶ (۱۹۶۲), issue 77, page 76-99.
- ↑ Byte Magazine Vol 6, Issue 6 (June 1981) p.۳۹۲) «The Impossible Dream: Computing e to ۱۱۶٬۰۰۰ places with a Personal Computer"
- ↑ Email from Robert Nemiroff and Jerry Bonnell - The Number e to 1 Million Digits
- ↑ «Email from Xavier Gourdon to Simon Plouffe - I have made a new e computation (with verification): ۱٬۲۵۰٬۰۰۰٬۰۰۰ digits». بایگانیشده از اصلی در ۲۱ مارس ۲۰۱۲. دریافتشده در ۲۱ آوریل ۲۰۱۱.
- ↑ PiHacks message 176 - calculation of E: World record by Shigeru Kondo[پیوند مرده]
- ↑ PiHacks message 177 - E to ۳٬۲۲۱٬۲۲۵٬۴۷۲ D[پیوند مرده]
- ↑ PiHacks message 1062 - New world record computation of E: ۲۵٬۱۰۰٬۰۰۰٬۰۰۰ digits[پیوند مرده]
- ↑ PiHacks message 1071 - Two new records: 50 billions for E and 25 billions for pi[پیوند مرده]
- ↑ ۳۴٫۰ ۳۴٫۱ «English Version of PI WORLD». بایگانیشده از اصلی در ۱۸ اوت ۲۰۱۱. دریافتشده در ۲۱ آوریل ۲۰۱۱.
- ↑ Announcing 500 billion digits of e...
- ↑ A list of notable large computations of e
- ↑ ۳۷٫۰ ۳۷٫۱ ۳۷٫۲ ۳۷٫۳ ۳۷٫۴ A list of notable large computations of e|
- ↑ "e" (به انگلیسی). numberworld.org. 5 December 2020. Retrieved 23 January 2023.


 French
French Deutsch
Deutsch









































![{\displaystyle e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce0cd8eb0003d22f6e68f69c95cf434c43bebc58)




















![{\displaystyle f(x)={\sqrt[{x}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e15600c8e263f973cca6db5347531ea5a6846aa8)






















