Analyse en composantes principales — Wikipédia
| Type | Méthode statistique (d), statistique multivariée |
|---|---|
| Noms courts | ACP, (en) PCA |
| Aspect de |
L'analyse en composantes principales (ACP ou PCA en anglais pour principal component analysis), ou, selon le domaine d'application, transformation de Karhunen–Loève (KLT)[1] ou transformation de Hotelling, est une méthode de la famille de l'analyse des données qui consiste à transformer des variables liées entre elles (dites « corrélées » en statistique) en nouvelles variables décorrélées les unes des autres. Ces nouvelles variables sont nommées « composantes principales » ou axes principaux. Elle permet de résumer l'information en réduisant le nombre de variables.
Il s'agit d'une approche à la fois géométrique[2] (les variables étant représentées dans un nouvel espace, selon des directions d'inertie maximale) et statistique (la recherche portant sur des axes indépendants expliquant au mieux la variabilité — la variance — des données). Lorsqu'on veut comprimer un ensemble de variables aléatoires, les premiers axes de l'analyse en composantes principales sont un meilleur choix, du point de vue de l'inertie ou de la variance.
L'outil mathématique est appliqué dans d'autres domaines que les statistiques et est parfois appelé décomposition orthogonale aux valeurs propres ou POD (anglais : proper orthogonal decomposition).
Histoire
[modifier | modifier le code]
L'ACP prend sa source dans un article de Karl Pearson publié en 1901[3]. Le père du test du χ² y prolonge ses travaux dans le domaine de la régression et des corrélations entre plusieurs variables. Pearson utilise ces corrélations non plus pour expliquer une variable à partir des autres (comme en régression), mais pour décrire et résumer l'information contenue dans ces variables.
Toutefois, c'est dans les années 1930 que l'ACP est formalisée par l'économiste et statisticien américain Harold Hotelling[4]. Il développe par la suite l'analyse canonique des corrélations, généralisation des analyses factorielles dont fait partie l'ACP.
Les champs d'application de l'ACP sont aujourd'hui multiples, allant de la biologie à la recherche économique et sociale, et plus récemment le traitement d'images et l'apprentissage automatique. L'ACP est majoritairement utilisée pour :
- décrire et visualiser des données ;
- les décorréler, la nouvelle base étant constituée d'axes qui ne sont pas corrélés entre eux ;
- les débruiter, en considérant que les axes que l'on décide d'oublier sont des axes bruités.
- effectuer une réduction de dimension des données d'entrainement en apprentissage automatique.
Sous le nom de « méthode de décomposition orthogonale aux valeurs propres », elle est également utilisée :
- pour réduire la taille de modèle d'éléments finis[5].
Quelques exemples introductifs
[modifier | modifier le code]
Premier exemple
[modifier | modifier le code]On considère un objet en trois dimensions et on cherche à le représenter le mieux possible par projection en deux dimensions. L'ACP va alors déterminer les deux axes de projection qui expliquent le mieux la dispersion de l'objet, autrement dit l'inertie du nuage des points qui le compose. Ainsi, comme dans la figure ci-contre, la projection des points du poisson en 3D sur le plan 2D formé par ces deux axes respectera au mieux la forme du nuage de point initial. En d'autres termes, il s'agit de trouver le plan de projection sur lequel la forme du poisson sera la plus étendue et reconnaissable possible.
Second exemple
[modifier | modifier le code]On possède des données sur les températures moyennes mensuelles de différentes villes de France et on cherche à résumer le climat français[6]. Intuitivement, les villes les plus chaudes en janvier le sont aussi en juillet. Les variables sont donc corrélées positivement entre elles et l'ACP mettra en évidence un premier axe opposant les villes chaudes aux villes froides. Toutefois, ces variables ne sont pas parfaitement corrélées car il existe des différences entre les villes dans l'écart entre les températures hivernales et estivales. L'ACP dégagera alors un second axe opposant les villes selon l'amplitude des températures :climat océanique ou climat continental.
Données
[modifier | modifier le code]On applique généralement une ACP sur un ensemble de N variables aléatoires X1, …, XN connues à partir d'un échantillon de réalisations conjointes de ces variables.
Cet échantillon de ces N variables aléatoires peut être structuré dans une matrice M, à K lignes et N colonnes :
Chaque variable aléatoire Xn, dont X1, n, …, XK, n sont des réalisations indépendantes, a une moyenne et un écart type σXn.
Poids
[modifier | modifier le code]Chaque réalisation conjointe des variables est associée à un poids . Ces poids, qui sont des nombres positifs dont la somme vaut 1, sont représentés par une matrice diagonale D de taille K :
Dans le cas le plus courant, les poids sont égaux et où est la matrice identité. Toutefois, on peut parfois vouloir appliquer des poids différents (cas des échantillons redressés, des données regroupées...).
Transformations de l'échantillon
[modifier | modifier le code]Le vecteur est le centre de gravité du nuage de points ; on le note souvent g. On a où désigne le vecteur de dont toutes les coordonnées sont égales à 1.
La matrice M est généralement centrée sur le centre de gravité :
- .
Elle peut être aussi réduite :
- .
Le choix de réduire ou non le nuage de points (i.e. les K réalisations de la variable aléatoire (X1, …, XN)) est un choix de modèle :
- si l'on ne réduit pas le nuage : une variable à forte variance va « tirer » tout l'effet de l'ACP à elle ;
- si l'on réduit le nuage : une variable qui n'est qu'un bruit va se retrouver avec une variance apparente égale à une variable informative.
Si les variables aléatoires sont dans des unités différentes, la réduction est obligatoire.
Calcul des covariances et des corrélations
[modifier | modifier le code]Dans le cas de poids uniformes (), une fois la matrice transformée en ou , il suffit de la multiplier par sa transposée pour obtenir:
- la matrice de variance-covariance des X1, …, XN si M n'est pas réduite : ;
- la matrice de corrélation des X1, …, XN si M est réduite : .
Ces deux matrices sont carrées (de taille N), symétriques, et réelles. Elles sont donc diagonalisables dans une base orthonormée en vertu du théorème spectral.
De façon plus générale, dans le cas de poids non uniformes, la matrice de variance-covariance s'écrit .
De plus, si l'on note la matrice diagonale des inverses des écarts-types:
alors on a:
- .
La matrice des coefficients de corrélation linéaire entre les N variables prises deux à deux, notée R, s'écrit:
- .
Critère d'inertie
[modifier | modifier le code]Dans la suite de cet article, nous considèrerons que le nuage est transformé (centré et réduit si besoin est). Chaque Xn est donc remplacé par ou . Nous utiliserons donc la matrice pour noter ou suivant le cas.
Le principe de l'ACP est de trouver un axe u, issu d'une combinaison linéaire des Xn, tel que la variance du nuage autour de cet axe soit maximale.
Pour bien comprendre, imaginons que la variance de u soit égale à la variance du nuage; on aurait alors trouvé une combinaison des Xn qui contient toute la diversité du nuage original (en tout cas toute la part de sa diversité captée par la variance).
Un critère couramment utilisé est la variance de l'échantillon (on veut maximiser la variance expliquée par le vecteur u). Pour les physiciens, cela a plutôt le sens de maximiser l'inertie expliquée par u (c'est-à-dire minimiser l'inertie du nuage autour de u).
Projection
[modifier | modifier le code]Etant donné un vecteur unitaire u, nous cherchons finalement u tel que la projection du nuage sur ait une variance maximale. La projection de l'échantillon des X sur u s'écrit :
la variance empirique de vaut donc :
où C est la matrice de covariance.
Comme nous avons vu plus haut que C est diagonalisable dans une base orthonormée, notons P le changement de base associé et la matrice diagonale formée de son spectre :
Les valeurs de la diagonale de sont rangées en ordre décroissant. Le vecteur unitaire u qui maximise est un vecteur propre de C associé à la valeur propre ; on a alors :
La valeur propre est la variance empirique sur le premier axe de l'ACP.
Il est aussi possible de démontrer ce résultat en maximisant la variance empirique des données projetées sur u sous la contrainte que u soit de norme 1 (par un multiplicateur de Lagrange ) :
On continue la recherche du deuxième axe de projection w sur le même principe en imposant qu'il soit orthogonal à u.
Diagonalisation
[modifier | modifier le code]La diagonalisation de la matrice de corrélation (ou de covariance si on se place dans un modèle non réduit), nous a permis d'écrire que le vecteur qui explique le plus d'inertie du nuage est le premier vecteur propre. De même le deuxième vecteur qui explique la plus grande part de l'inertie restante est le deuxième vecteur propre, etc.
Nous avons vu en outre que la variance expliquée par le k-ième vecteur propre vaut λk.
Finalement, la question de l'ACP se ramène à un problème de diagonalisation de la matrice de corrélation.
Optimisation numérique
[modifier | modifier le code]Numériquement, la matrice M étant rectangulaire, il peut être plus économique de la décomposer en valeurs singulières, puis de recombiner la décomposition obtenue, plutôt que de diagonaliser M' M.
ACP et variables qualitatives
[modifier | modifier le code]En ACP, il est fréquent que l’on veuille introduire des variables qualitatives supplémentaires. Par exemple, on a mesuré de nombreuses variables quantitatives sur des plantes. Pour ces plantes, on dispose aussi de variables qualitatives, par exemple l’espèce à laquelle appartient la plante. On soumet ces données à une ACP des variables quantitatives. Lors de l’analyse des résultats, il est naturel de chercher à relier les composantes principales à la variable qualitative espèce. Pour cela on produit les résultats suivants :
- identification, sur les plans factoriels, des différentes espèces en les représentant par exemple par des couleurs différentes ;
- représentation, sur les plans factoriels, des centres de gravité des plantes appartenant à une même espèce ;
- indication, pour chaque centre de gravité et pour chaque axe, d'une probabilité critique pour juger de la significativité de l’écart entre un centre de gravité et l’origine.
Tous ces résultats constituent ce que l’on appelle introduire une variable qualitative en supplémentaire. Cette procédure est détaillée dans Escofier&Pagès 2008, Husson, Lê & Pagès 2009 et Pagès 2013.
Peu de logiciels offrent cette possibilité de façon « automatique ». C’est le cas de SPAD[7] qui historiquement, à la suite des travaux de Ludovic Lebart, a été le premier logiciel à le proposer, et de R avec le package FactoMineR[8].
Résultats théoriques
[modifier | modifier le code]Si les sections précédentes ont travaillé sur un échantillon issu de la loi conjointe suivie par X1, …, XN, que dire de la validité de nos conclusions sur n'importe quel autre échantillon issu de la même loi ?
Plusieurs résultats théoriques permettent de répondre au moins partiellement à cette question, essentiellement en se positionnant par rapport à une distribution gaussienne comme référence.
Méthodes voisines et extensions : la famille factorielle
[modifier | modifier le code]L’analyse en composantes principales est la plus connue des méthodes factorielles ; d’autres méthodes factorielles existent pour analyser d’autres types de tableau. À chaque fois, le principe général est le même :
- on considère deux nuages de points, l’un associé aux lignes du tableau analysé et l’autre aux colonnes de ce tableau ;
- ces deux nuages sont liés par des relations de dualité : ils ont la même inertie totale ;
- chacun de ces nuages est projeté sur ses directions d’inertie maximum ;
- d’un nuage à l’autre, les directions d’inertie de même rang sont liées par des relations de dualité (ou de transition) : elles ont la même inertie et les coordonnées des projections sur l’une se déduisent des coordonnées des projections sur l’autre.
Elle s’applique à des tableaux de contingence c'est-à-dire des tableaux croisant deux variables qualitatives. Ce type de tableau est très différent de celui analysé par ACP : en particulier, les lignes et les colonnes jouent des rôles symétriques alors que la distinction entre lignes et colonnes (c'est-à-dire entre individus et variables) est majeure en ACP.
Elle s’applique à des tableaux dans lesquels un ensemble d’individus est décrit par un ensemble de variables qualitatives. Ce type de tableau est donc voisin de celui analysé en ACP, les variables quantitatives étant remplacées par des variables qualitatives. L’ACM est souvent vue comme un cas particulier de l’ACP mais ce point de vue est très réducteur. L’ACM possède suffisamment de propriétés spécifiques pour être considérée comme une méthode à part entière.
On peut aussi présenter l’ACM à partir de l’ACP comme cela est fait dans Pagès 2013. L’intérêt est de relier entre eux les ressorts de l’ACP et ceux de l’ACM ce qui ouvre la voie au traitement simultané des deux types de variables (cf. AFDM et AFM ci-après)
Les données sont constituées par un ensemble d’individus pour lesquels on dispose de plusieurs variables, comme en ACP ou en ACM. Mais, ici, les variables sont aussi bien quantitatives que qualitatives. L’analyse factorielle de données mixtes traite simultanément les deux types de variables en leur faisant jouer un rôle actif. L’AFDM est décrite dans Pagès 2013 et Escofier&Pagès 2008.
Les données sont, ici encore, constituées par un ensemble d’individus pour lesquels on dispose de plusieurs variables. Mais cette fois, outre qu’elles peuvent être quantitatives et/ou qualitatives, les variables sont structurées en groupes. Ce peut être, par exemple, les différents thèmes d’un questionnaire. L’AFM prend en compte cette structure en groupes dans l’analyse de ces données. L’AFM est décrite en détail dans Pagès 2013 et Escofier&Pagès 2008.
Il est souvent difficile d’interpréter les composantes principales lorsque les données comprennent beaucoup de variables d’origines pluridisciplinaires, ou lorsque certaines variables sont qualitatives. Cela conduit l’utilisateur de l’ACP à une délicate élimination de plusieurs variables. Si des observations ou des variables ont un impact excessif sur la direction des axes, il convient de les retirer et de les projeter ensuite en éléments supplémentaires. De plus, il faut éviter d'interpréter les proximités entre les points proches du centre du plan factoriel.
L’iconographie des corrélations, au contraire, qui n’est pas une projection sur un système d’axes (ce n'est donc pas une analyse factorielle), ne présente pas ces inconvénients. On peut donc conserver toutes les variables.
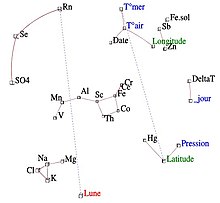
Le principe du diagramme est de souligner les corrélations « remarquables » de la matrice de corrélation, par un trait plein (corrélation positive) ou pointillé (corrélation négative). Une forte corrélation n’est pas « remarquable » si elle n’est pas directe, mais causée par l’effet d’une tierce variable. Inversement de faibles corrélations peuvent être « remarquables ». Par exemple, si une variable Y dépend de plusieurs variables indépendantes, les corrélations de Y avec chacune d’entre elles sont faibles et pourtant « remarquables ».
Analyse en composantes principales à noyaux
[modifier | modifier le code]L'analyse en composantes principales à noyaux consiste à appliquer l'astuce du noyau pour permettre de réaliser une ACP non linéaire, en projetant les données dans un espace à grande dimension[9].
Applications
[modifier | modifier le code]Compression
[modifier | modifier le code]L'analyse en composantes principales est usuellement utilisée comme outil de compression linéaire. Le principe est alors de ne retenir que les n premiers vecteurs propres issus de la diagonalisation de la matrice de corrélation (ou covariance), lorsque l'inertie du nuage projeté sur ces n vecteurs représente qn pour cent de l'inertie du nuage original, on dit qu'on a un taux de compression de 1 - qn pour cent, ou que l'on a compressé à qn pour cent. Un taux de compression usuel est de 20 %.
Les autres méthodes de compressions statistiques habituelles sont:
- l'analyse en composantes indépendantes ;
- les cartes auto-adaptatives (SOM, self organizing maps en anglais) ; appelées aussi cartes de Kohonen ;
- l'analyse en composantes curvilignes ;
- la compression par ondelettes.
Il est possible d'utiliser le résultat d'une ACP pour construire une classification statistique des variables aléatoires X1, …, XN, en utilisant la distance suivante (Cn, n' est la corrélation entre Xn et Xn' ):
Analyse de séries dynamiques d'images
[modifier | modifier le code]L'ACP, désignée en général dans le milieu du traitement du signal et de l'analyse d'images plutôt sous son nom de « transformée de Karhunen-Loève » (TKL) est utilisée pour analyser les séries dynamiques d'images[10], c'est-à-dire une succession d'images représentant la cartographie d'une grandeur physique, comme les scintigraphies dynamiques en médecine nucléaire, qui permettent d'observer par gamma-caméra le fonctionnement d'organes comme le cœur ou les reins.
Dans une série de P images, chaque pixel est considéré comme un point d'un espace affine de dimension P dont les coordonnées sont la valeur du pixel pour chacune des P images au cours du temps. Le nuage ainsi formé par tous les points de l'image peut être analysé par l'ACP, (il forme un hyper-ellipsoïde à P dimensions) ce qui permet de déterminer ses axes principaux.
En exprimant tous les points dans le repère orthogonal à P dimensions des axes de l'ACP, on passe ainsi de la série temporelle d'origine (les pixels représentent la valeur en fonction du temps) à une nouvelle série (également de P images) dans l'espace de Karhunen-Loève : c'est la Transformée de Karhunen-Loève, qui est une opération réversible : on parle de « TKL » et de « TKL inverse » ou « TLK-1 ».
La compression est possible car l'information est contenue presque entièrement sur les premiers axes de l'ACP. Mais la notion de « compression » sous-entend que les autres images correspondant aux autres axes sont volontairement ignorées. La TKL étant réversible, la suppression arbitraire des axes les moins énergétiques constitue alors un filtrage permettant de réduire le bruit temporel de la série d'images.
Concrètement, l'application de TKL + suppression des axes les moins significatifs + TKL-1 permet de supprimer le fourmillement apparent (bruit temporel) d'une série animée d'images.
En imagerie médicale fonctionnelle, on améliore ainsi la qualité visuelle de la visualisation scintigraphique du cycle cardiaque moyen.
Par ailleurs, l'analyse de l'importance respective des valeurs propres de l'ACP permet d'approcher le nombre de fonctionnements physiologiques différents. On a ainsi pu montrer que le cœur sain peut être entièrement représenté avec deux images (deux axes de l'ACP contiennent toute l'information utile), alors que pour certaines pathologies l'information utile s'étale sur 3 images[11].
Analyse d'images multi-spectrales
[modifier | modifier le code]Comme pour l'application précédente, la longueur d'onde remplaçant juste le temps, la TKL a été proposée à plusieurs reprises pour extraire l'information utile d'une série d'images monochromes représentant les intensités pour des longueurs d'onde différentes. De telles images peuvent être issues de microscopie optique classique, confocale ou SNOM (Microscope optique en champ proche)[12].
Évolution de la topographie
[modifier | modifier le code]De la même manière, la TKL permet de mettre en évidence des cinétiques différentes lors de l'analyse topographique dynamique, c'est-à-dire l'analyse de l'évolution du relief au cours du temps. Elle permet alors de déceler des phénomènes invisibles par simple observation visuelle, mais se distinguant par une cinétique légèrement différente (par exemple pollution d'une surface rugueuse par un dépôt)[13].
Apprentissage automatique
[modifier | modifier le code]L'ACP est une des techniques permettant la réduction de dimension, très utile en apprentissage automatique pour améliorer la qualité des modèles, et faciliter leur calcul[14].
Logiciels
[modifier | modifier le code]R
[modifier | modifier le code]Le package R FactoMineR inclut, en particulier, outre l'ACP, toutes les extensions décrites plus haut : AFC, ACM, AFDM et AFM). Ce logiciel est relié au livre Husson, Lê & Pagès 2009.
Les packages ade4[15] et adegraphics permettent d'analyser et visualiser (ACP inter, intra classe, etc.) des données issues de problèmes biologiques[16][source secondaire souhaitée].
Exemple sous R
[modifier | modifier le code]L'objectif est de réaliser une ACP sur des données physico-chimiques récoltées par 30 stations le long du Doubs[17].
Il y a sept variables physico-chimiques d’intérêt, mesurées au niveau des 30 stations : le pH, la dureté de l’eau, le phosphate, le nitrate, l'ammoniaque, l'oxygène et la demande biologique en oxygène. Quelles données sont corrélées ? Peut-on représenter la pollution le long de la rivière ?
Les données étant exprimées dans des unités différentes, nous avons intérêt à réaliser une ACP normée (centrée et réduite) sur les 7 variables physico-chimiques.
library(ade4) library(adegraphics) data(doubs) ACP <- dudi.pca(doubs$env[,5:11], center = T, scale = T, scannf=FALSE, nf = 2) #On récupère les 5 variables physico-chimiques, on centre les données, on les réduit, on définit le nombre d'axes pour l'ACP à 2) ACP$eig #On récupère les valeurs propres s.corcircle(ACP$co, xax = 1, yax = 2) #On affiche le cercle des corrélations sur le premier plan factoriel de l'ACP s.label(ACP$li, xax = 1, yax = 2) #On affiche les stations dans le premier plan factoriel de l'ACP s.value(doubs$xy,ACP$li[,1], symbol = "circle", col = c("blue","brown"))#Les stations sont symbolisées par des cercles pour la valeur du 1er axe de l'ACP (la pollution). Les stations peu polluées sont en bleu, les stations plus polluées sont en marron L'interprétation de l'ACP sur le premier axe du [18] montre une corrélation négative entre le taux d'oxygène et la présence de polluants. Avec [19], on peut représenter les stations avec leurs valeurs sur cet axe de pollution, symbolisées par des cercles de différentes couleurs.
- Figures pour l'exemple d'ACP sous R
- Stations le long du Doubs.
- Le cercle de corrélation (corcircle) tracé pour le premier plan factoriel de l'ACP sur les données du Doubs. Le premier axe montre une corrélation négative entre l'oxygène et 3 polluants connus : nitrates (nit), phosphates (pho), ammoniaque (amm). On peut dire que cet axe est caractérisé par la pollution. Les eaux riches en oxygène n'ont pas de polluants et inversement. Le deuxième axe est un axe caractérisé essentiellement par le pH.
- Après interprétation du cercle des corrélations, on peut dire que les stations 25, 23, 24 sont les plus polluées. La station 15 a un pH élevé.
- Chaque station est remplacée par un cercle prenant la valeur du résultat de l'ACP sur le premier axe. Le cercle des corrélations a indiqué qu'il s'agit d'un axe de pollution. On remarque que la deuxième partie du fleuve est plus polluée que la première partie. La station 25 a la valeur de pollution maximale. Cela est cohérent avec les observations du 1er plan factoriel de l'ACP.
Notes et références
[modifier | modifier le code]- ↑ http://tcts.fpms.ac.be/cours/1005-07-08/codage/codage/xcodim2.pdf
- ↑ Une vidéo d’introduction à l’ACP fondée sur la géométrie est accessible ici.
- ↑ (en) Pearson, K., « On Lines and Planes of Closest Fit to Systems of Points in Space », Philosophical Magazine, vol. 2, no 6, , p. 559–572 (lire en ligne [PDF])
- ↑ (en) « Analysis of a Complex of Statistical Variables with Principal Components », 1933, Journal of Educational Psychology.
- ↑ « introduction to model reduction », sur Scilab, (consulté le ).
- ↑ « Cours d'ACP : théorie et pratique » (consulté le )
- ↑ http://www.coheris.com/produits/analytics/logiciel-data-mining/
- ↑ (en) Sébastien Lê, « FactoMineR : Exploratory Multivariate Data Analysis with R », sur factominer.free.fr (consulté le ).
- ↑ Schölkopf, « Nonlinear Component Analysis as a Kernel Eigenvalue Problem », Neural Computation, vol. 10, no 5, , p. 1299–1319 (DOI 10.1162/089976698300017467, S2CID 6674407, CiteSeerx 10.1.1.100.3636).
- ↑ Évaluation de la perfusion et de la fonction contractile du myocarde à l’aide de l’analyse de Karhunen-Loève en tomographie d’émission monophotonique myocardique synchronisée à l’ECG par P. Berthout, R. Sabbah, L. Comas, J. Verdenet, O. Blagosklonov, J.-C. Cardot et M. Baud dans Médecine nucléaire Volume 31, Volume 12, décembre 2007, Pages 638-646.
- ↑ Baud, Cardot, Verdenet et al, Service de médecine nucléaire, Hôpital Jean-Minjoz, boulevard Fleming, 25030 Besançon cedex, France (nombreuses publications sur plus de 30 ans)
- ↑ Analysis of optical near-field images by Karhunen—Loève transformation Daniel Charraut, Daniel Courjon, Claudine Bainier, and Laurent Moulinier, Applied Optics, Vol. 35, Issue 20, p. 3853-3861 (1996)
- ↑ (en) Jean-Yves Catherin, Measure in 2D, visualise in 3D and understand in 4D dans Micronora Informations juin 2008, page 3
- ↑ (en-US) Jason Brownlee, « How to Calculate Principal Component Analysis (PCA) from Scratch in Python », sur Machine Learning Mastery, (consulté le )
- ↑ Daniel Chessel, Stephane Dray, Anne Beatrice Dufour, Jean Thioulouse, Simon Penel, « Accueil ade4 », sur pbil.univ-lyon1.fr (consulté le ).
- ↑ Jean Thioulouse, Stéphane Dray, Anne-Béatrice Dufour, Aurélie Siberchicot, Thibaut Jombart et Sandrine Pavoine, Multivariate Analysis of Ecological Data with ade4, New York, Springer, , 330 p. (ISBN 978-1-4939-8848-8).
- ↑ « R: Pair of Ecological Tables », sur pbil.univ-lyon1.fr (consulté le )
- ↑ « R: Plot of the factorial maps of a correlation circle », sur pbil.univ-lyon1.fr (consulté le )
- ↑ « R: Representation of a value in a graph », sur pbil.univ-lyon1.fr (consulté le )
Voir aussi
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]- Jean-Paul Benzécri ; Analyse des données. T2 (leçons sur l'analyse factorielle et la reconnaissance des formes et travaux du Laboratoire de statistique de l'Université de Paris 6. T. 2 : l'analyse des correspondances), Dunod Paris Bruxelles Montréal, 1973
- Jean-Paul Benzécri et Al. Pratique de l'analyse des données. T1 (analyse des correspondances. Exposé élémentaire), Dunod Paris, 1984,
- Jean-Paul Benzécri et Al. Pratique de l'analyse des données. T2 (abrégé théorique. Études de cas modèle), Dunod Paris, 1984
- Brigitte Escofier et Jérôme Pagès, Analyses factorielles simples et multiples : objectifs, méthodes et interprétation, Paris, Dunod, Paris, 2008, 4e éd. (1re éd. 1988), 318 p. (ISBN 978-2-10-051932-3)
- François Husson, Sébastien Lê et Jérôme Pagès, Analyse des données avec R, Presses Universitaires de Rennes, , 224 p. (ISBN 978-2-7535-0938-2)
- Ludovic Lebart, Morineau Alain, Piron Marie; Statistique exploratoire multidimensionnelle, Dunod Paris, 1995
- Jérôme Pagès, Analyse factorielle multiple avec R, Les Ulis, EDP sciences, Paris, , 253 p. (ISBN 978-2-7598-0963-9)
- Mathieu Rouaud ; Probabilités, statistiques et analyses multicritères Un livre de 290 pages qui traite de l'ACP (les principes et de nombreux exemples concernant, entre autres, les isolants thermiques et les eaux minérales). Version numérique libre et gratuite.
- Michel Volle, Analyse des données, Economica, 4e édition, 1997, (ISBN 2-7178-3212-2)
Articles connexes
[modifier | modifier le code]- Valeurs propres
- Compression statistique
- Équilibre biais / variance
- Analyse de la variance
- Partitionnement de données
- Exploration de données
- Iconographie des corrélations
- Michel Loève
- Kari Karhunen
- Théorème de Karhunen-Loève (en)
- Analyse discriminante linéaire


 French
French Deutsch
Deutsch






















































