0,999… — Wikipédia

En mathématiques, le développement décimal périodique qui s'écrit 0,999…, que l'on dénote encore par ou ou , représente un nombre réel dont on peut montrer que c'est le nombre 1. En d'autres termes, les deux notations 0,999… et 1 sont deux notations différentes pour le même nombre. Les démonstrations mathématiques de cette identité ont été formulées avec des degrés variés de rigueur mathématique, et selon les préférences relatives à la définition des nombres réels, les hypothèses sous-jacentes, le contexte historique et le public visé.
Le fait que certains nombres réels peuvent être représentés par plus d'une chaîne de « décimales » n'est pas limité au système décimal, c'est-à-dire de base dix. Le même phénomène a lieu dans toutes les bases entières, et les mathématiciens ont aussi repéré la manière d'écrire 1 dans des systèmes à base non entière. Ce phénomène n'est d'ailleurs pas spécifique au nombre 1 : tout nombre décimal non nul a une écriture finie et une autre écriture avec une infinité de 9, comme 18,32 = 18,31999…. L'écriture avec un nombre fini de décimales est plus simple, et est presque toujours celle que l'on préfère, ce qui contribue au préjugé que c'est la « seule » représentation. Cependant, l'autre forme, avec une infinité de décimales, est parfois plus utile pour la compréhension du développement décimal de certaines fractions, ou, en base 3, pour caractériser l'ensemble de Cantor. La forme « non unique » doit être prise en compte dans certaines démonstrations du fait que l'ensemble des réels n'est pas dénombrable. Plus généralement, tout système de représentation numérique positionnelle pour les nombres réels contient une infinité de nombres ayant des représentations multiples.
L'égalité 0,999… = 1 est depuis longtemps acceptée par les mathématiciens et enseignée dans les manuels. Ce n'est que dans les dernières décennies que les chercheurs en enseignement des mathématiques ont étudié comment les élèves perçoivent cette égalité. Certains la rejettent, à cause de leur « intuition » que chaque nombre a un développement décimal unique, qu'il doit y avoir des nombres infinitésimaux non nuls, ou bien que le développement 0,999… finit par se terminer. Ces intuitions sont erronées dans le système des nombres réels, mais il existe d'autres systèmes de nombres qui peuvent en admettre certaines.
Démonstrations algébriques
[modifier | modifier le code]Il existe plusieurs démonstrations élémentaires de l'égalité 0,999… = 1.
Fractions et divisions posées
[modifier | modifier le code]L'une des raisons de la nécessité des développements décimaux infinis est la représentation décimale des fractions. Poser une division d'entiers telle que 1/9 donne un développement décimal 0,111… dans lequel les décimales se répètent sans fin. Cette égalité donne une démonstration rapide de 0,999… = 1 :
Sous une autre forme[1], on peut multiplier les deux membres de l'égalité 13 = 0,333… par 3, pour obtenir d'une part 3 × 13 = 1 et d'autre part 3 × 0,333… = 0,999…. Ces deux nombres sont donc bien égaux.
Manipulation des décimales
[modifier | modifier le code]Quand un nombre en notation décimale est multiplié par 10, les chiffres ne changent pas, mais le séparateur des unités est décalé d'un cran vers la droite. Ainsi, 10 × 0,999… = 9,999…. La suite demande un tout petit peu d'algèbre[1],[2],[3] :
Discussion
[modifier | modifier le code]« Alors que cette preuve établit que 0,999… = 1, elle ne semble rien offrir expliquant pourquoi cette égalité est vraie. [… Cependant,] en arithmétique élémentaire, ce genre de démonstration peut aider à expliquer pourquoi 0,33… ≠ 0,4, tandis que 0,99… est égal à 1,0. Ou encore, en algèbre élémentaire, [… à expliquer] une méthode générale pour trouver la fraction correspondant à un développement décimal périodique[3] ». Mais ces démonstrations ne mettent pas en lumière les relations fondamentales entre les développements décimaux et les nombres qu'ils représentent, relations qui sont sous-jacentes au sens même à donner à l'égalité entre deux développements décimaux.
William Byers pense qu'un élève qui admet que 0,999… = 1 à cause des démonstrations précédentes, mais qui n'a pas résolu l'ambiguïté de la notation 0,999… — qui, selon lui, désigne à la fois un processus de sommation et un objet mathématique — ne peut pas comprendre vraiment l'égalité[1].
Une fois qu'un système de représentation est défini, il peut être utilisé pour justifier les règles d'arithmétique décimale utilisées dans les démonstrations précédentes. De plus, on peut démontrer directement que les expressions 0,999… et 1,000… représentent toutes deux le même nombre réel, car cela fait partie de la définition (voir infra).
Démonstrations analytiques
[modifier | modifier le code]Puisque l'examen de 0,999… n'intervient aucunement dans la formalisation des mathématiques, on peut le différer jusqu'à ce que soient établis les théorèmes standards de l'analyse réelle.
Il faut avant tout donner un sens à l'écriture des nombres réels, en notation décimale, sous la forme d'un éventuel signe –, d'une suite finie de chiffres formant l'entier naturel b0 partie entière de la valeur absolue, d'un séparateur décimal, et d'une suite éventuellement infinie (bi)i ≥ 1 de chiffres qui peuvent prendre les valeurs de 0 à 9, formant la partie fractionnaire de cette même valeur absolue. Dans cette notation positionnelle, il est essentiel que, contrairement à la partie entière b0, la partie fractionnaire ne soit pas limitée à un nombre fini de chiffres.
Pour discuter de 0,999…, on n'utilise pas l'éventualité d'un signe –, donc on se borne à un développement décimal de la forme b0,b1b2b3….
Séries et suites infinies
[modifier | modifier le code]La présentation peut-être la plus courante des développements décimaux est de les définir comme des séries infinies. En général :
Pour 0,999…, on peut appliquer le théorème de convergence des séries géométriques : si |r| < 1, alors :
Comme 0,999… est une somme de ce genre, avec r = 110, le théorème résout rapidement la question :

Cette démonstration (en fait celle de 9,999… = 10) apparaît dès 1770 dans les Éléments d'algèbre de Leonhard Euler[4], mais la sommation d'une série géométrique est elle-même un résultat plus ancien. Une démonstration typique du XVIIIe siècle utilisait une manipulation terme à terme analogue à la manipulation des décimales donnée plus haut ; Bonnycastle, en 1811, utilise ce genre d'argument pour justifier que 0,999… = 1[5].
Une réaction du XIXe siècle contre ce genre de méthodes cavalières de sommation a abouti à la définition encore dominante aujourd'hui :
- la somme d'une série est la limite de la suite de ses sommes partielles ;
- une suite (x0, x1, x2, …) admet une limite x si la distance |x – xn| devient arbitrairement petite quand n s'accroît.
Avec ces définitions, la démonstration du théorème ci-dessus consiste à calculer la distance entre la limite escomptée, x = a1 – r, et les sommes partielles de la série géométrique, xn = a + ar + … + arn. On trouve que cette distance est une suite géométrique de raison r, donc de limite nulle (puisque |r| < 1)[note 1].
Dans le cas particulier de 0,999… = 1, cette démonstration s'écrit simplement :
Avant cette formalisation, elle était ébauchée en termes plus imagés, mais moins précis. Par exemple, en 1846, Davies explique « .999 +, continué à l'infini = 1, parce que l'addition de chaque nouveau 9 rapproche la valeur de 1[6]. » ; Smith et Harrington, en 1895, écrivent : « quand on prend un grand nombre de 9, la différence entre 1 et 0,999… devient petite de façon inconcevable[7]. » De telles approches heuristiques sont souvent interprétées par les étudiants comme impliquant que 0,999… est lui-même strictement inférieur à 1.[réf. nécessaire]
Segments emboîtés et bornes supérieures
[modifier | modifier le code]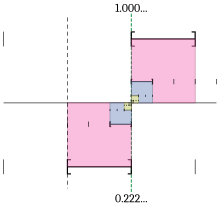
La représentation ci-dessus par des séries est un moyen simple de définir le nombre réel associé à un développement décimal. Pour s'assurer que cette notation n'abuse pas du signe « = », on a utilisé les propriétés des limites. Mais d'autres constructions utilisent celles de l'ordre.
L'une d'elles s'appuie sur le théorème des segments emboîtés (voir troisième construction), qui dit que pour une suite de segments emboîtés dont les longueurs deviennent arbitrairement petites, l'intersection de ces intervalles contient exactement un point. Le nombre b0,b1b2b3… est donc défini comme l'unique réel appartenant à tous les segments [b0, b0 + 1], [b0,b1, b0,b1 + 0,1], etc. Ainsi, 0,999… est l'unique réel qui se trouve dans tous les segments [0, 1], [0,9, 1], [0,99, 1], [0,999, 1], etc. c'est-à-dire le réel 1[8].
Le processus inverse est de déterminer, pour un nombre réel donné, tous les développements décimaux auxquels il correspond. Si l'on sait qu'un nombre réel x est dans le segment [0, 10] (c'est-à-dire que 0 ≤ x ≤ 10), on peut diviser cet intervalle en 10 parties égales, qui ne se recouvrent qu'à leurs extrémités : [0, 1], [1, 2], [2, 3], … , [9, 10]. Le nombre x doit appartenir à l'un de ces intervalles ; s'il appartient à [2, 3], on note le chiffre 2, et l'on subdivise l'intervalle en dix : [2,0, 2,1], [2,1, 2,2], [2,2, 2,3], … , [2,9, 3]. On note alors le séparateur décimal et le chiffre correspondant à l'intervalle où se trouve x ; en continuant ce processus, on obtient une suite infinie de segments emboîtés, que l'on repère par une suite infinie de chiffres b0,b1b2b3… et l'on écrit x = b0,b1b2b3…. Dans ce formalisme, les identités 0,999… = 1 et 1,000… = 1 reflètent respectivement que 1 est à la fois dans le segment [0, 1] et [1, 2], si bien que l'on peut choisir l'un ou l'autre de ces intervalles au début de la recherche des décimales. La suite découle de ce choix initial.
Le théorème des segments emboîtés est d'habitude basé sur un caractère plus fondamental des nombres réels : l'existence du plus petit majorant, appelé borne supérieure (ou supremum). Pour exploiter directement ce genre d'objet, on peut définir b0,b1b2b3… comme la borne supérieure de l'ensemble des approximants b0, b0,b1, b0,b1b2, b0,b1b2b3, etc.[9],[10]. On peut montrer ensuite que cette définition (ou celle par les segments emboîtés) est cohérente avec la procédure de subdivision, ce qui implique à nouveau que 0,999… = 1. Tom Apostol conclut : « Le fait qu'un nombre réel puisse avoir deux représentations décimales différentes est simplement un reflet de ce que deux ensembles différents de nombres réels peuvent avoir la même borne supérieure[11]. ».
Démonstrations à partir de la construction des nombres réels
[modifier | modifier le code]Certaines approches définissent explicitement les nombres réels comme étant des structures basées sur les nombres rationnels, en utilisant la théorie axiomatique des ensembles. Les nombres naturels : 0, 1, 2, etc. commencent par 0 et continuent en croissant, si bien que chaque nombre a un successeur. On peut étendre les nombres naturels par les entiers négatifs, pour obtenir tous les entiers, puis à leurs rapports, ce qui donne les nombres rationnels. Ces systèmes de nombres sont accompagnés par l'arithmétique des quatre opérations de base, l'addition, la soustraction, la multiplication et la division. De façon plus subtile, ils incluent la notion d'ordre, si bien qu'un nombre peut être comparé à un autre, et trouvé supérieur, inférieur ou égal à ce dernier.
Le passage des rationnels aux réels est une extension majeure. Il existe au moins deux manières courantes d'aboutir à ce résultat, toutes deux publiées en 1872 : les coupures de Dedekind et les suites de Cauchy. Les démonstrations de 0,999… = 1 qui utilisent directement ces constructions ne se trouvent pas dans les manuels d'analyse réelle, où la tendance dans les dernières décennies a été d'utiliser l'analyse axiomatique. Même si une construction est proposée, elle est généralement utilisée à démontrer les axiomes des nombres réels, qui à leur tour permettent les démonstrations données ci-dessus. Cependant, certains auteurs expriment l'idée qu'il serait logiquement préférable de commencer par une construction, et que les démonstrations qui en découlent seront plus autonomes[note 2].
Les coupures de Dedekind
[modifier | modifier le code]La définition des nombres réels comme coupures de Dedekind a été publiée pour la première fois par Richard Dedekind en 1872[12]. Dans la reformulation désormais classique (cf. article détaillé), une coupure est une partie propre non vide de l'ensemble des rationnels[note 3], stable par minorant et ne possédant pas de plus grand élément[note 4]. Un réel est alors représenté par l'ensemble infini de tous les rationnels qui lui sont strictement inférieurs. Tout développement décimal positif définit facilement une coupure de Dedekind : l'ensemble des rationnels strictement inférieurs à une certaine troncature du développement. Par exemple, la coupure correspondant au développement infini 0,999… est l'ensemble des rationnels inférieurs à 0, ou à 0,9, ou à 0,99, etc., et celle correspondant au développement fini 1 est l'ensemble des rationnels strictement inférieurs à 1. Ces deux ensembles sont égaux donc les deux développements décimaux 0,999… et 1 représentent le même réel, par définition.
Suites de Cauchy
[modifier | modifier le code]Une autre démarche pour construire les nombres réels utilise moins directement la notion d'ordre des rationnels. C'est la définition à partir des suites de Cauchy de rationnels, publiée pour la première fois en 1872, indépendamment, par Eduard Heine et Georg Cantor[12].
On commence par définir la « distance » entre deux rationnels x et y comme la valeur absolue |x − y|, c'est-à-dire le plus grand des deux rationnels x – y et y – x (cette distance est donc un rationnel positif).
Dans ce cadre, les réels sont définis comme les suites de rationnels (x0, x1, x2, …) qui sont « de Cauchy pour cette distance », c'est-à-dire telles que pour tout rationnel δ > 0, il existe un entier N tel que |xm − xn| ≤ δ pour tout m et n supérieurs à N. En d'autres termes, la distance entre deux termes devient plus petite que n'importe quel rationnel positif à partir d'un certain rang[13].
On définit de même, dans ce contexte, la notion de suite de rationnels convergeant vers 0, en n'utilisant que des δ > 0 rationnels. Puis, si (xn) et (yn) sont deux suites de Cauchy, on dit qu'elles sont égales en tant que nombres réels si leur différence (xn – yn) converge vers 0. Les troncatures du développement décimal b0,b1b2b3… forment une suite de nombres décimaux (donc rationnels) qui est de Cauchy. Elle est prise comme la valeur du nombre[14]. Dans ce formalisme, l'égalité 0,999… = 1 vient donc simplement[15], comme dans l'approche précédente par les séries, du fait que la suite des rationnels
c'est-à-dire la suite des puissances de 110, converge vers 0 (au sens a priori plus faible défini ici : pour tout rationnel δ > 0, on a 110n ≤ δ pour tout entier n assez grand).
Généralisations
[modifier | modifier le code]Le résultat 0,999… = 1 se généralise facilement dans deux directions. Premièrement, tout nombre non nul qui a un développement décimal fini (suivi d'une infinité de zéros), a un autre développement qui se termine par une infinité de 9. Par exemple, 0,25 (= 0,25000…) est égal à 0,24999…, exactement comme 1 (= 1,000…) est égal à 0,999…. Ces nombres sont les nombres décimaux. Ils forment, comme on vient de le voir, une partie dense de l'ensemble des réels.
Deuxièmement, le même phénomène se produit dans toutes les bases. Par exemple en base deux, 0,111… = 1, et en base trois, 0,222… = 1. Les manuels d'analyse réelle ont tendance à sauter le système décimal et à commencer par présenter l'une de ces généralisations, ou les deux[16].
Le nombre 1 possède aussi plusieurs représentations dans des bases non entières. Par exemple, dans le système de numération en base d'or (celui qui admet le nombre d'or φ comme base) les deux représentations standard de l'unité sont 1,000… et 0,101010…, et 1 possède en outre une infinité dénombrable de représentations non standard, c'est-à-dire contenant des 1 adjacents ; pour tout q strictement compris entre 1 et φ, la situation est encore pire : l'ensemble des développements de 1 en base q a la puissance du continu (donc est infini non dénombrable) ; à l'opposé, dans l'intervalle ]φ, 2[, les bases q dans lesquelles 1 n'a qu'un développement autre que le développement trivial 1,000… (comme dans les bases entières) forment un ensemble comaigre (qui a donc la puissance du continu)[17]. En 1998, Komornik et Loreti ont déterminé la plus petite de ces bases, la constante de Komornik-Loreti q = 1,787231650…. Dans cette base, 1 = 0,110100110010110… ; les décimales sont données par la suite de Prouhet-Thue-Morse, qui ne se répète pas[18].
Une généralisation bien plus profonde concerne les systèmes de numération positionnels les plus généraux. Ils admettent aussi des représentations multiples, et dans un certain sens, avec de pires difficultés. Par exemple[19] :
- dans le système ternaire équilibré, 1/2 = 0,111… = 1,111… ;
- dans le système factoriel (utilisant les bases 2!, 3!, 4!, … pour les positions après la virgule), 1 = 1,0000… = 0,1234…[note 5].
Marko Petkovšek[note 6] a proposé une définition générale de système positionnel et a montré que si un tel système représente tous les réels, l'ensemble des réels ayant plusieurs représentations est dense. Il appelle sa démonstration « un exercice instructif en topologie générale élémentaire » ; elle consiste à munir l'ensemble des suites de symboles dans un tel système d'une topologie adéquate, et à utiliser que l'espace des réels est de Baire[20].
Applications
[modifier | modifier le code]- Le théorème de Midy est un résultat d'arithmétique élémentaire sur l'apparition des 9 dans les développements décimaux périodiques de fractions dont les dénominateurs sont certains nombres premiers. Par exemple : 17 = 0,142857142857142857… et 1 + 8 = 4 + 5 = 2 + 7 = 9. Étienne Midy a démontré son théorème en 1836 et beaucoup de mathématiciens l'ont ensuite redécouvert et prolongé. L'une des démonstrations[note 7] s'appuie sur la généralisation suivante de l'égalité 0,999… = 1 : à partir d'un développement décimal 0,a1a2a3… d'un réel x compris entre 0 et 1, on obtient un développement 0,b1b2b3… de 1 – x en prenant comme chiffres les compléments à 9 de ceux de x : bi = 9 – ai.
- En analyse réelle, l'analogue en base trois, 0,222… = 1, apparaît dans le fait que l'ensemble de Cantor est fermé : un point dans l'intervalle unité [0, 1] fait partie de l'ensemble de Cantor s'il peut s'écrire en base 3 en n'utilisant que les chiffres 0 et 2. On obtient donc l'ensemble de Cantor en enlevant de [0, 1] son tiers central : l'intervalle de 0,1 = 13 à 0,1222… = 23 (mais en conservant ces extrémités puisqu'elles ont une autre représentation, qui ne contient pas de 1 : par exemple, 13 = 0,0222…) puis de même, en ôtant des deux segments latéraux leur tiers central (intervalle ouvert), etc.
- L'analogue en base deux, 0,111… = 1, apparaît lorsqu'on adapte un autre des travaux de Cantor — son argument de la diagonale de 1891 — pour démontrer que l'intervalle réel unité n'est pas dénombrable : si l'on raisonne en base n = 2, la prise en compte du double développement des fractions dyadiques nécessite des précautions. Mais ce problème disparaît dès qu'on choisit n > 2.
Scepticisme des étudiants
[modifier | modifier le code]Les étudiants en mathématiques rejettent souvent l'égalité de 0,999… et 1, pour des raisons allant de leur apparence différente à des doutes profonds concernant le concept de limite et aux désaccords sur la nature des infinitésimaux. Il y a beaucoup de facteurs qui contribuent en commun à cette confusion :
- Les étudiants sont souvent « mentalement attachés à la notion qu'un nombre peut être représenté d'une seule manière par un développement décimal ». La vue de deux développements décimaux manifestement différents du même nombre apparaît comme un paradoxe, qui est amplifié par l'apparition du nombre apparemment bien connu : 1[note 8].
- Certains étudiants interprètent 0,999…, ou toute notation semblable, comme une suite de 9, longue certes, mais finie, de longueur variable, non spécifiée. Dans la mesure où ils acceptent une suite infinie, ils s'attendent néanmoins à ce que le dernier chiffre « à l'infini » soit un 9[21],[22].
- L'intuition et un enseignement ambigu conduisent les étudiants à penser la limite d'une suite comme un processus, plutôt qu'une valeur fixe, puisqu'une suite n'a pas besoin d'atteindre sa limite. Quand les étudiants acceptent la différence entre une suite de nombres et sa limite, ils peuvent lire 0,999… comme la suite elle-même, plutôt que sa limite[23],[22].
Ces idées sont erronées dans le contexte de la théorie standard des nombres réels, bien que certaines puissent être valables dans d'autres systèmes numériques ; soit ceux-ci ont été inventés pour leur utilité générale en mathématiques, soit il s'agit de contre-exemples pour une meilleure compréhension de la nature de 0,999….
Beaucoup de ces explications ont été trouvées par David Tall (en), qui a étudié les caractéristiques de l'enseignement et de la connaissance, qui conduisent à certaines des incompréhensions qu'il a rencontrées chez ses étudiants à l'université[24]. En les interrogeant pour déterminer pourquoi une vaste majorité commençait par rejeter l'égalité, il a trouvé que « les étudiants continuent à concevoir 0,999… comme une suite de nombres qui se rapproche toujours plus de 1, mais pas comme une valeur fixée, au motif qu'« on n'a pas spécifié combien il y a de décimales », ou que « c'est le nombre décimal le plus proche en dessous de 1 »[22]. ».
Parmi les démonstrations élémentaires, la multiplication de 0,333… = 1/3 par 3 est apparemment une bonne stratégie[note 9] pour convaincre les étudiants réticents que 0,999… = 1. Cependant, quand on leur fait comparer leur approbation de la première équation avec leurs doutes sur la deuxième, certains étudiants commencent à douter de la première, d'autres s'énervent[25]. Les méthodes plus sophistiquées ne sont pas plus garanties : des étudiants qui sont tout à fait capables d'appliquer des définitions rigoureuses peuvent retomber sur le langage intuitif quand ils sont surpris par un résultat de mathématique tel que 0,999… = 1. Par exemple, une étudiante en analyse réelle était capable de montrer que 0,333… = 1/3 en utilisant la définition par la borne supérieure, mais soutenait que 0,999… n'est pas égal à 1, sur la base de sa compréhension initiale de 0,333… = 1/3 par la division posée[26]. D'autres encore peuvent démontrer que 0,333… = 1/3 mais, face à la démonstration par les fractions, insistent sur le fait que la « logique » prend le pas sur les calculs.
Joseph Mazur (en) raconte l'histoire d'un de ses étudiants en analyse numérique, par ailleurs brillant, qui « mettait en doute à peu près tout ce que je disais en cours, mais ne doutait jamais de sa calculette et qui avait fini par croire que neuf chiffres étaient tout ce dont on a besoin pour faire des mathématiques, y compris calculer la racine carrée de 23. Cet étudiant restait réfractaire à un argument de limite pour 9,999… = 10, l'appelant un « processus infiniment croissant sauvagement imaginé »[27] ».
Selon sa théorie APOS (Actions, Processes, Objects, Schemas) de l'apprentissage mathématique, Dubinsky et ses collaborateurs[28] proposent une explication : les étudiants qui perçoivent 0,999… comme une suite finie, indéterminée, dont la distance à 1 est infiniment petite, « n'ont pas fini de construire un concept du développement décimal infini ». D'autres étudiants qui ont fini de construire ce concept, ne sont sans doute pas capables d'encapsuler ce concept dans un concept d'objet, comme celui qu'ils ont pour 1, et ils voient donc ces deux concepts comme incompatibles. Dubinsky et al. relient aussi cette capacité mentale d'encapsulation au fait de considérer une fraction comme 1/3 comme un nombre véritable, et ainsi de travailler avec les ensembles de nombres.
Dans la culture populaire
[modifier | modifier le code]Avec le développement d'Internet, les débats sur 0,999… sont sortis de la salle de classe, et se trouvent fréquemment sur les forums de discussion ou d'annonces, y compris beaucoup qui n'ont en principe que peu à voir avec les mathématiques.
- Dans le forum sci.math[29], la discussion sur 0,999… est devenue un « sport de masse », et c'est une des questions abordées dans ses FAQ[30]. La FAQ passe rapidement sur 1/3, la multiplication par 10, les limites, et fait même allusion aux suites de Cauchy.
- Une édition de 2003 de la chronique générale The Straight Dope du Chicago Reader discute 0,999… au moyen de 1/3 et des limites, et parle des malentendus intérieurs en ces termes :
« Le primate inférieur qui est en nous résiste encore, disant que 0,999… ne représente pas vraiment un nombre, mais à la rigueur un processus. Pour trouver un nombre, il faut arrêter le processus, mais alors l'histoire de 0,999… = 1 s'effondre. N'importe quoi[31]... »
- Dans le même esprit la question de 0,999… s'est trouvée un tel succès pendant les sept premières années du forum Battle.net de la société Blizzard Entertainment que la compagnie a émis un communiqué de presse le 1er avril 2004, pour affirmer définitivement que c'est 1 :
« Nous sommes très excités de fermer ce livre une fois pour toutes. Nous avons été témoins des peines de cœur et des soucis pour savoir si, oui ou non, 0,999… = 1, et nous sommes fiers d'annoncer que la démonstration suivante résout finalement et de façon conclusive pour nos clients[32]. »
- Deux démonstrations sont alors proposées, basées sur les limites et sur la multiplication par 10.
- 0,999… fait aussi partie du folklore mathématique, et tout spécialement dans la plaisanterie suivante[33] :
« Question : Combien faut-il de mathématiciens pour visser une ampoule électrique ?
Réponse : 0,999999… »
Dans les systèmes de numération alternatifs
[modifier | modifier le code]Bien que les nombres réels forment un système de nombres extrêmement utile, la décision d'interpréter la notation 0,999… comme la représentation d'un nombre réel n'est, tout bien pesé, qu'une convention, et Timothy Gowers[34] argumente que l'identité 0,999… = 1 qui en résulte est une convention aussi :
« On peut définir d'autres systèmes de numération utilisant de nouvelles règles, ou de nouveaux objets ; dans ce genre de systèmes, les preuves ci-dessus devraient être réinterprétées, et on pourrait bien trouver que dans tel ou tel système 0,999… et 1 ne soient pas identiques. Cependant, beaucoup de systèmes sont des extensions – ou des alternatives – par rapport au système des nombres réels, et 0,999… = 1 continue à être vrai. Mais même dans ce genre de système, cela vaut la peine d'examiner le comportement de 0,999… (dans la mesure où cette représentation a un sens, et en plus unique), mais aussi pour le comportement de phénomènes reliés. Si ces phénomènes diffèrent de ceux du système des nombres réels, alors au moins une des hypothèses de base de ce système est fausse. »
Nombres infinitésimaux
[modifier | modifier le code]Certaines démonstrations que 0,999… = 1 reposent sur la propriété archimédienne des nombres réels standards : il n'y a pas d'infinitésimaux non nuls. Il existe des structures algébriques mathématiquement cohérentes, comprenant diverses alternatives aux réels standards, qui ne sont pas archimédiennes. La signification de 0,999… dépend de la structure dans laquelle on l'utilise. Par exemple les nombres duaux possèdent un nouvel élément, infinitésimal, , analogue dans les nombres complexes à l'unité imaginaire i, sauf que dans le cas des nombres duaux, . La structure qui en résulte peut servir en dérivation algorithmique. Les nombres duaux peuvent être ordonnés par un ordre lexicographique, auquel cas les multiples de deviennent des éléments non archimédiens[35]. Noter, cependant que, considérés comme une extension des réels, les duaux satisfont encore 0,999… = 1. Noter encore que puisque existe en tant que nombre dual, existe aussi, si bien que n'est pas « le plus petit nombre dual positif », et d'ailleurs, comme pour les réels, ce nombre n'existe pas.
L'analyse non standard fournit un système de numération avec tout un ensemble d'infinitésimaux (et leurs inverses, infiniment grands)[note 10]. A. H. Lightstone a mis au point un développement décimal pour les nombres hyperréels dans l'intervalle [36]. Il montre comment associer à tout nombre une suite de décimales 0,d1d2d3…;…d∞–1d∞d∞+1… indexée par les nombres hypernaturels. Bien qu'il ne discute pas directement 0,999…, il montre que le nombre réel 1/3 est représenté par 0,333…;…333…, ce qui est une conséquence de l'axiome de transfert. En multipliant par 3, on obtient une représentation analogue pour des développements avec des 9 qui se répètent. Mais Lightstone montre que dans ce système, les expressions 0,333…;…000… — ou 0,999…;…000… — ne correspondent à aucun nombre.
En même temps, le nombre hyperréel avec la dernière décimale 9 à un rang hypernaturel infini H satisfait à l'inégalité stricte . En fait, la suite : et . Selon cette écriture, Karin et Mikhail Katz ont proposé une évaluation différente de 0,999… :
où est un hypernaturel infini donné par la suite , modulo un certain ultrafiltre[37]. Ian Stewart caractérise cette interprétation comme une façon « tout à fait raisonnable » de justifier rigoureusement l'intuition qu'il « manque un petit quelque chose entre 0,999… et 1 »[38]. Comme Karin et Mikhail Katz, Robert Ely met en question la supposition que les idées des étudiants sur l'inégalité 0,999… < 1 sont des idées fausses sur les nombres réels, et il préfère les interpréter comme des intuitions non standard, qui pourraient avoir un intérêt dans l'apprentissage du calcul infinitésimal[39].
Hackenbush
[modifier | modifier le code]La théorie des jeux combinatoires fournit également des nombres alternatifs aux réels, avec le jeu Hackenbush L-R infini comme exemple particulièrement frappant. En 1974, Elwyn Berlekamp décrit une correspondance entre les chaînes du jeu Hackenbush et les développements binaires des réels, motivé par l'idée de la compression de données. Par exemple, la valeur de la chaîne Hackenbush LRRLRLRL… est . Cependant la valeur de LRLLL… (correspondant à est infinitésimalement inférieur à 1. La différence entre les deux est le nombre surréel , où est le premier ordinal infini ; la représentation correspondante est LRRRR…, ou [note 11].
Brisure de la soustraction
[modifier | modifier le code]Une autre manière par laquelle les démonstrations peuvent être rendues invalides est le cas où n'existe tout simplement pas, parce que la soustraction n'est pas toujours possible. Les structures mathématiques où il existe une opération d'addition, mais où l'opération de soustraction n'est pas toujours définie comprennent les demi-groupes commutatifs, les monoïdes commutatifs et les demi-anneaux. Fred Richman considère un tel système — construit de façon que 0,999… < 1 — dans un article intitulé « 0,999… est-il égal à 1 ? »[2] de Mathematics Magazine, un journal destiné aux enseignants en premier cycle de l'université et à leurs étudiants.
Sur les développements décimaux[note 12] positifs, Richman définit l'ordre lexicographique et une opération d'addition, remarquant que 0,999… < 1, tout simplement parce que 0 < 1 au rang des unités, mais pour tout développement infini x, on a 0,999… + x = 1 + x. Donc une particularité des développements décimaux est qu'ils ne sont pas tous simplifiables pour l'addition. Une autre est qu'il n'y a pas de développement décimal x correspondant à 1/3, c'est-à-dire vérifiant x + x + x = 1. Après avoir défini la multiplication, les développements décimaux positifs forment un demi-anneau positif, totalement ordonné et commutatif[2]. Bien que cette structure vérifie certaines propriétés intéressantes, beaucoup des règles de l'arithmétique usuelle n'y sont plus valables.
En parallèle, Richman propose une variante paradoxale des coupures de Dedekind : il innove en appelant « coupure de Dedekind » de l'anneau D des nombres décimaux toute partie propre non vide A de D stable par minorant, mais sans interdire que A possède un plus grand élément. À tout élément d de D, il peut ainsi associer deux « coupures » : l'ensemble , qu'il note d–, et l'ensemble , qu'il assimile à d et nomme « coupure principale ». Rappelant que Dedekind identifiait l'une à l'autre ces deux « coupures » en disant qu'elles « ne diffèrent que de façon inessentielle » — ce qui revient à exclure la seconde, comme dans la présentation classique des coupures de Dedekind rappelée ci-dessus, Richman analyse cependant la structure où toutes ses « coupures de Dedekind » sont autorisées et où d– et d ne sont pas considérées comme égales. Ses « coupures » contenant 0 sont alors en bijection avec les développements décimaux positifs, en associant à tout développement l'ensemble des nombres décimaux inférieurs au sens large à une certaine troncature du développement. L'ensemble correspondant au développement infini 0,999… est donc la coupure 1–, tandis que l'ensemble correspondant au développement 1 est la « coupure principale 1 ».
Il n'y a pas d'infinitésimaux positifs dans ses « coupures » sur D, mais il y a une sorte d'« infinitésimal négatif » 0–, qui n'a pas de développement décimal. Il conclut que 0,999… = 1 + 0–, tandis que l'équation 0,999… + x = 1 n'a pas de solution[note 13].
Nombres p-adiques
[modifier | modifier le code]Quand on leur pose des questions sur 0,999…, les novices croient souvent qu'il doit y avoir un « dernier 9 », ce qui fait qu'ils pensent que est un nombre positif, qu'ils écrivent 0,000…1. Que cela ait ou non un sens, le but intuitif est clair : si l'on ajoute un 1 au dernier des 9 cela va provoquer des retenues en cascade, remplacer tous les 9 par des 0 et le 0 des unités par un 1. Parmi d'autres raisons, cette idée échoue, parce qu'il n'y a pas de « dernier 9 » dans 0,999…[40]. Cependant il existe un système qui contient une infinité de 9 y compris un dernier 9.

Les nombres p-adiques sont un système de numération alternatif de grand intérêt en théorie des nombres. Comme les nombres réels, les nombres p-adiques peuvent être construits à partir des rationnels, au moyen de suites de Cauchy ; la construction utilise une métrique différente, dans laquelle 0 est plus proche de p, et encore plus de pn, que de 1. Les nombres p-adiques forment un corps commutatif si p est premier, et un anneau commutatif sinon, y compris si p = 10. Donc on peut faire de l'arithmétique avec les nombres p-adiques, et il n'y a pas d'infinitésimaux.
Dans les nombres 10-adiques, les analogues des développements décimaux s'étendent vers la gauche. Le développement …999 possède un dernier 9 tandis qu'il n'a pas de premier 9. On peut ajouter 1 au chiffre des unités, et les retenues en cascade ne laissent que des 0 :
donc …999 = –1[41]. Une autre démonstration utilise une série géométrique. La série infinie impliquée par la notation …999 ne converge pas dans les réels, mais elle converge dans les 10-adiques, et l'on peut réutiliser la formule familière :
- [42].
– à comparer avec la série (voir supra).
Une troisième démonstration a été inventée par un élève de cinquième, qui doutait de l'argument de la limite donné par son professeur, que 0,999… = 1, mais était inspiré par la démonstration par la multiplication par 10 (voir supra), mais à l'envers : si alors , et par suite [41].
Une extension finale, puisque 0,999… = 1 dans les réels et …999 = –1 dans les 10-adiques, « par une foi aveugle et un jonglage inconsidéré avec les symboles »[43], on peut ajouter les deux relations, et arriver à …999,999… = 0. Cette équation n'a de sens ni comme développement 10-adique, ni comme développement décimal, mais il se trouve qu'on peut lui donner une signification si l'on développe une théorie des « doubles décimales », avec des côtés gauches périodiques, pour représenter un système familier : celui des nombres réels[44].
Problèmes connexes
[modifier | modifier le code]- Les paradoxes de Zénon, et en particulier celui d'Achille et de la tortue, sont voisins du paradoxe apparent que 0,999… = 1. Le paradoxe peut être modélisé mathématiquement, et comme 0,999…, résolu par une série géométrique. Cependant, il n'est pas clair que ce traitement mathématique s'applique aux questions d'ordre métaphysique que Zénon explorait[45].
- La division par zéro intervient dans certaines des discussions populaires de 0,999… et excite également des controverses. Tandis que la plupart des auteurs choisissent de définir 0,999…, presque tous les traitements modernes laissent indéfinie la division par zéro, parce qu'on ne peut pas lui assigner de signification dans le champ des nombres réels standards. Cependant, la division par zéro peut être définie dans certains autres systèmes, comme dans l'analyse complexe, où on peut ajouter un point à l'infini aux nombres finis pour obtenir la sphère de Riemann. Dans ce cas, cela a un sens de définir 1/0 comme l'infini[note 14] ; et, en fait, les résultats sont profonds et applicable à de nombreux problèmes en ingénierie et en physique. Certains mathématiciens éminents avaient plaidé pour ce genre de définition bien avant que l'un de ces systèmes de numération ne soit mis au point[46].
- Le zéro négatif est encore un exemple de redondance dans l'écriture des nombres. Dans des systèmes de numération tels que les réels, où 0 dénote l'élément neutre pour l'addition, il n'est ni positif ni négatif, et l'interprétation usuelle de -0 est que c'est l'élément symétrique de 0 pour l'addition, ce qui force -0 = 0[47]. Néanmoins, certaines applications scientifiques utilisent des zéros positif et négatif distincts. En informatique, il existe des standards de codage des entiers stockés sous la forme de signe et valeur absolue, et c'est également la règle pour les nombres à virgule flottante, spécifiés par le standard IEEE 754 pour les virgules flottantes[48]. On peut également citer le complément à un, toutefois en désuétude. Ce qu'il faut retenir, c'est que si la plupart du temps les systèmes savent qu'ils doivent répondre « vrai » à la question « est-ce que 0 = -0 ? », cela peut provoquer des résultats différents, surtout en cas de division par 0.[pertinence contestée]
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]- ↑ Les diverses démonstrations de cette dernière étape utilisent inévitablement l'une des caractérisations axiomatiques du corps des nombres réels.
- ↑ La synthèse historique est revendiquée par Griffiths et Hilton 1970, p. xiv, puis par Pugh 2002, p. 10 ; en fait les deux préfèrent les coupures de Dedekind aux axiomes. Pour l'utilisation des coupures dans les manuels, voir Pugh 2002, p. 10 ou Rudin 1976, p. 17. Pour les points de vue sur la logique, voir Pugh 2002, p. 10, Rudin 1976, p. ix ou Munkres 2000, p. 30.
- ↑ Richman 1999 remarque qu'on peut remplacer les rationnels par n'importe quel sous-anneau Partie dense, en particulier l'anneau des nombres décimaux.
- ↑ Richman 1999 explique : « Pourquoi fait-on cela ? Précisément pour éliminer la possibilité de l'existence de nombres distincts et 1 […] Nous voyons donc que dans la définition traditionnelle des nombres réels, l'équation est incorporée dès le début. ».
- ↑ En effet, est égal à la série télescopique
- ↑ Mathématicien slovène né en 1955, élève de Dana Scott, co-auteur de Herbert Wilf et Doron Zeilberger, et professeur à l'université de Ljubljana.
- ↑ Voir le § « Cas p non premier » de l'article sur le théorème de Midy.
- ↑ Bunch 1982, p. 119, Tall et Schwarzenberger 1978, p. 6. La dernière suggestion est due à Burrell 1998, p. 28 : « Le plus rassurant de tous les nombres est peut-être 1. […] Il est donc particulièrement dérangeant de voir quelqu'un faire passer 0,9… pour 1. »
- ↑ Richman 1999 pense que cet argument « tire sa force du fait que les gens ont été conditionnés à accepter la première ligne sans y réfléchir ».
- ↑ Pour un traitement complet des nombres non standard, voir par exemple Robinson 1996.
- ↑ Berlekamp, Conway et Guy 1982, p. 79–80, 307–311 discutent 1 et 1/3, et abordent . Le jeu pour découle directement de la règle de Berlekamp, et est discuté par Walker 1999.
- ↑ Qu'il appelle « nombres décimaux », tandis qu'il nomme « fractions décimales » ce qu'on appelle couramment nombres décimaux.
- ↑ Richman 1999. Rudin 1976, p. 23 donne cette construction alternative (étendue à tous les rationnels) comme dernier exercice de son chapitre I.
- ↑ Voir par exemple le traitement des transformations de Möbius dans Conway 1978, p. 47–57.
Références
[modifier | modifier le code]- Byers 2007, p. 39-41.
- Richman 1999.
- Peressini et Peressini 2007, p. 186.
- ↑ (en) Leonhard Euler (trad. du français par John Hewlett et Francis Horner), Elements of Algebra, Orme Longman, , 3e éd. (1re éd. 1770) (ISBN 0387960147, lire en ligne), p. 170.
- ↑ Grattan-Guinness 1970, p. 69 ; (en) John Bonnycastle, An Introduction to Algebra, (lire en ligne), p. 177.
- ↑ (en) Charles Davies, The University Arithmetic : Embracing the Science of Numbers, and Their Numerous Applications, A. S. Barnes, (lire en ligne), p. 175.
- ↑ Smith et Harrington 1895, p. 115.
- ↑ Bartle et Sherbert 1982, p. 60-62 ; Pedrick 1994, p. 29 ; Sohrab 2003, p. 46 ; Stewart et Tall 1977, p. 34.
- ↑ Apostol 1974, p. 9, 11-12 ; Rosenlicht 1985, p. 27.
- ↑ (en) Richard Beals, Analysis : An Introduction, Cambridge University Press, , 261 p. (ISBN 978-0-521-60047-7, lire en ligne), p. 22.
- ↑ Apostol 1974, p. 12.
- (en) John J. O'Connor et Edmund F. Robertson, « The real numbers: Stevin to Hilbert », sur MacTutor, université de St Andrews..
- ↑ Griffiths et Hilton 1970, §24.2, « Sequences », p. 386.
- ↑ Griffiths et Hilton 1970, p. 388, 393.
- ↑ Griffiths et Hilton 1970, p. 395.
- ↑ Protter et Morrey 1991, p. 503 ; Bartle et Sherbert 1982, p. 61.
- ↑ (en) Paul Erdős, Miklos Horváth et István Joó, « On the uniqueness of the expansions 1 = ∑q–ni », Acta Math. Hungar., vol. 58, no 3, , p. 333-342 (DOI 10.1007/BF01903963).
- ↑ Komornik et Loreti 1998, p. 636.
- ↑ Petkovšek 1990, p. 409-410.
- ↑ Petkovšek 1990.
- ↑ Tall et Schwarzenberger 1978, p. 6-7.
- Tall 2000, p. 221.
- ↑ Tall et Schwarzenberger 1978, p. 6.
- ↑ (en) David Tall, « Limits, infinitesimals and infinities », sur Université de Warwick.
- ↑ Tall 1976, p. 10-14.
- ↑ Edwards et Ward 2004, p. 416–417. Pour un exemple analogue, voir Pinto et Tall 2001, p. 5.
- ↑ Mazur 2005, p. 137–141.
- ↑ (en) Ed Dubinsky, Kirk Weller, Michael McDonald et Anne Brown, « Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2 », Educational Studies in Mathematics, vol. 60, , p. 253-266 (DOI 10.1007/s10649-005-0473-0) (p. 261-262).
- ↑ de Vreught 1994, repris dans Why does 0.9999... = 1 ?, sur mathforum.org.
- ↑ Comme l'a observé Richman 1999, citant de Vreught 1994.
- ↑ Adams 2003.
- ↑ (en) « Blizzard Entertainment Announces .999~ (Repeating) = 1 », Blizzard Entertainment, .
- ↑ Renteln et Dundes 2005, p. 27.
- ↑ Gowers 2002.
- ↑ Berz 1992, p. 439–442.
- ↑ Lightstone 1972, p. 245–247.
- ↑ Katz et Katz 2010a.
- ↑ Stewart 2009, p. 175 ; la discussion de 0,999… est étendue sur les p. 172-175.
- ↑ Katz et Katz 2010b ; Ely 2010.
- ↑ Gardiner 2003, p. 98, Gowers 2002, p. 60.
- Fjelstad 1995, p. 11.
- ↑ Fjelstad 1995, p. 14–15.
- ↑ DeSua 1960, p. 901.
- ↑ DeSua 1960, p. 902–903.
- ↑ Wallace 2003, p. 51, Maor 1987, p. 17.
- ↑ Maor 1987, p. 54.
- ↑ Munkres 2000, Exercise 1 (c), p. 34.
- ↑ (en) Herbert Kroemer et Charles Kittel, Thermal Physics, New York, W. H. Freeman, , 2e éd., 473 p. (ISBN 0-7167-1088-9), p. 462 ; (en) MSDN, « Floating point types », .
Ouvrages et articles cités
[modifier | modifier le code]- (en) Cecil Adams, « An infinite question: Why doesn't .999~ = 1? », The Straight Dope,
- (en) Tom M. Apostol, Mathematical Analysis, Addison-Wesley, , 2e éd., 492 p. (ISBN 0-201-00288-4) — Passage de l'analyse élémentaire à l'analyse avancée, ce livre a l'ambition d'être « honnête, rigoureux, à jour, et en même temps, pas trop pédant. » (préface). Les développements d'Apostol sur les nombres réels utilisent l'axiome de la borne supérieure et introduisent les développements décimaux deux pages plus loin (p. 9-11).
- (en) R. G. Bartle et D. R. Sherbert, Introduction to Real Analysis, Wiley, (ISBN 0-471-05944-7) — Ce manuel vise à être « un manuel accessible, de rythme raisonnable, qui traite des concepts et techniques fondamentaux de l'analyse réelle ». Son développement sur les réels repose sur l'axiome de la borne supérieure (p. vii-viii).
- (en) Elwyn R. Berlekamp, J. H. Conway et R. K. Guy, Winning Ways for your Mathematical Plays, Academic Press, (ISBN 0-12-091101-9)
- (en) Martin Berz, « Automatic differentiation as nonarchimedean analysis », dans L. Atanassova et J. Herzberger, Computer Arithmetic and Enclosure Methods, Elsevier, (lire en ligne), p. 439-450
- (en) Bryan H. Bunch, Mathematical Fallacies and Paradoxes, Van Nostrand Reinhold, , 216 p. (ISBN 0-442-24905-5) — Ce livre présente une analyse des paradoxes et faussetés, comme un outil pour explorer son sujet central « la relation assez ténue entre réalité mathématique et réalité physique ». Il suppose connue l'algèbre de seconde ; les mathématiques supplémentaires sont apportées par le livre, y compris les séries géométriques au chapitre 2. Bien que 0,999… ne soit pas l'un des paradoxes entièrement traités, il est brièvement mentionné au cours d'un développement sur la méthode de Cantor (p. ix-xi, 119).
- (en) Brian Burrell, Merriam-Webster's Guide to Everyday Math : A Home and Business Reference, Merriam-Webster, , 373 p. (ISBN 0-87779-621-1, lire en ligne)
- (en) William Byers, How Mathematicians Think : Using Ambiguity, Contradiction, and Paradox to Create Mathematics, Princeton University Press, , 415 p. (ISBN 978-0-691-12738-5 et 0-691-12738-7, lire en ligne)
- (en) John B. Conway (en), Functions of One Complex Variable I, Springer, coll. « GTM » (no 11), , 2e éd. (1re éd. 1973), 317 p. (ISBN 978-0-387-90328-6, lire en ligne) — Ce texte suppose « un solide cours de calcul analytique » comme préalable ; ses buts avoués sont de présenter l'analyse complexe comme « une introduction aux mathématiques » et d'en expliciter les matières avec clarté et précision (p. vii).
- (en) Frank C. DeSua, « A system isomorphic to the reals », American Mathematical Monthly, vol. 67, no 9, , p. 900-903 (DOI 10.2307/2309468)
- (en) Barbara Edwards et Michael Ward, « Surprises from mathematics education research: Student (mis)use of mathematical definitions », American Mathematical Monthly, vol. 111, no 5, , p. 411-425 (lire en ligne)
- (en) Robert Ely, « Nonstandard student conceptions about infinitesimals », Journal for Research in Mathematics Education, vol. 41, no 2, , p. 117-146 — Cet article est une étude de terrain concernant une étudiante, qui a mis au point une théorie des infinitésimaux à la Leibniz, pour s'aider à comprendre le calcul différentiel, et en particulier pour rendre compte du fait que 0,999… diffère de 1 par une valeur infinitésimale 0,000…1.
- (en) George B. Thomas, Ross Finney, Maurice D. Weir et Frank R. Giordano, Thomas' Calculus : Early Transcendentals, New York, Addison-Wesley, , 10e éd.
- (en) Paul Fjelstad, « The repeating integer paradox », The College Mathematics Journal, vol. 26, no 1, , p. 11-15 (DOI 10.2307/2687285)
- (en) Anthony Gardiner, Understanding Infinity : The Mathematics of Infinite Processes, Dover, (1re éd. 1982), 308 p. (ISBN 0-486-42538-X, lire en ligne)
- (en) Timothy Gowers, Mathematics : A Very Short Introduction, Oxford, Oxford University Press, , 143 p. (ISBN 0-19-285361-9, lire en ligne)
- (en) Ivor Grattan-Guinness, The Development of the Foundations of Mathematical Analysis from Euler to Riemann, MIT Press, (ISBN 0-262-07034-0)
- (en) H. B. Griffiths et P. J. Hilton, A Comprehensive Textbook of Classical Mathematics : A Contemporary Interpretation, Londres, Van Nostrand Reinhold, , 640 p. (ISBN 978-0-387-90342-2, lire en ligne) — Ce livre est l'aboutissement d'un cours pour les professeurs de mathématiques du secondaire dans la région de Birmingham. Le cours était destiné à donner une perspective universitaire sur l'enseignement des mathématiques à l'école, et le livre vise les étudiants « qui ont en gros le niveau demandé après une année d'études spécialisées en mathématiques à l'université ». Les nombres réels sont construits au chapitre 24, « chapitre peut-être le plus difficile de tout le livre », bien que les auteurs attribuent une bonne partie de la difficulté à leur utilisation de la théorie des idéaux, qui n'est pas reproduite ici (p. vii, xiv). Ce livre est écrit spécialement pour permettre un deuxième regard sur des concepts familiers, avec un éclairage contemporain (p. viii).
- (en) K. Katz et M. Katz, « When is .999… less than 1 ? », The Montana Mathematics Enthusiast, vol. 7, no 1, , p. 3-30 (lire en ligne)
- (en) Karin Usadi Katz et Mikhail G. Katz, « Zooming in on infinitesimal 1 − .9.. in a post-triumvirate era », Educational Studies in Mathematics, vol. 74, no 3, , p. 259-273 (DOI 10.1007/s10649-010-9239-4, arXiv 1003.1501)
- (en) Vilmos Komornik et Paola Loreti, « Unique developments in non-integer bases », American Mathematical Monthly, vol. 105, no 7, , p. 636-639 (DOI 10.2307/2589246)
- (en) A. H. Lightstone, « Infinitesimals », American Mathematical Monthly, vol. 79, no 3, , p. 242-251 (DOI 10.2307/2316619)
- (en) Eli Maor, To Infinity and Beyond : A Cultural History of the Infinite, Birkhäuser, , 275 p. (ISBN 3-7643-3325-1, lire en ligne) — Revue de l'infini, par thèmes plutôt que chronologique, ce livre est « destiné au lecteur généraliste », mais « raconté du point de vue d'un mathématicien ». À propos du dilemme entre rigueur et lisibilité, l'auteur « espère avoir convenablement résolu ce problème » (p. x-xiii).
- (en) Joseph Mazur, Euclid in the Rainforest : Discovering Universal Truths in Logic and Math, Pearson: Pi Press, , 334 p. (ISBN 0-13-147994-6)
- (en) James Munkres, Topology, Prentice Hall, , 2e éd. (1re éd. 1975), 537 p. (ISBN 978-0-13-181629-9, lire en ligne) — Pensé comme une introduction à la topologie, « au niveau du 2e cycle universitaire », sans connaissances préalables : « je ne suppose même pas que le lecteur en connaisse beaucoup en théorie des ensembles » (p. xi). Le traitement des réels par Munkres est axiomatique ; il prétend construire à la main : « Cette manière d'approcher le sujet demande pas mal de temps et d'efforts, et cela a une valeur plus logique que mathématique. » (p. 30).
- (en) Rafael Núñez, « Do Real numbers really move? Language, thought, and gesture: the embodied cognitive foundations of mathematics », dans Reuben Hersh, 18 Unconventional Essays on the Nature of Mathematics, Springer, (ISBN 978-0-387-25717-4, lire en ligne), p. 160-181
- (en) George Pedrick, A First Course in Analysis, Springer, , 279 p. (ISBN 0-387-94108-8, lire en ligne)
- (en) Anthony Peressini et Dominic Peressini, « Philosophy of mathematics and mathematics education », dans Bart van Kerkhove et Jean Paul van Bendegem, Perspectives on Mathematical Practices, Springer, coll. « Logic, Epistemology, and the Unity of Science » (no 5), (ISBN 978-1-4020-5033-6, lire en ligne), p. 175-189
- (en) Marko Petkovšek, « Ambiguous numbers are dense », American Mathematical Monthly, vol. 97, no 5, , p. 408-411 (DOI 10.2307/2324393)
- (en) Márcia Pinto et David Tall, Following Students'Development in a Traditional University Analysis Course, PME25, (lire en ligne), v4: 57-64
- (en) M. H. Protter et Charles B. Morrey, A First Course in Real Analysis, Springer, , 2e éd. (1re éd. 1977), 536 p. (ISBN 978-0-387-97437-8, lire en ligne) — Ce livre vise à « présenter une fondation théorique de l'analyse convenable pour les étudiants qui ont terminé un cours standard sur le calcul analytique » (p. vii). À la fin du chapitre 2, les auteurs supposent comme axiome pour les réels que les suites croissantes majorées convergent, démontrant plus tard le théorème des segments emboîtés et la propriété de la borne supérieure (p. 56-64). Les développements décimaux apparaissent dans l'appendice 3, « développements des réels dans une base quelconque » (p. 503-507).
- (en) Charles Chapman Pugh, Real Mathematical Analysis, Springer, , 440 p. (ISBN 978-0-387-95297-0, lire en ligne) — Supposant le lecteur familier avec les rationnels, Pugh introduit les coupures de Dedekind dès que possible, disant du traitement axiomatique : « Ceci est une sorte d'entourloupe, puisque toute l'analyse est fondée sur le système des réels. » (p. 10). Après avoir démontré la propriété de la borne supérieure et quelques faits connexes, les coupures ne sont plus utilisées pour le reste du livre.
- (en) Paul Renteln et Alan Dundes, « Foolproof: a sampling of mathematical folk humor », Notices of the AMS, vol. 52, no 1, , p. 24-34 (lire en ligne)
- (en) Fred Richman, « Is 0.999… = 1? », Mathematics Magazine, vol. 72, no 5, , p. 396-400 (lire en ligne)
- (en) Abraham Robinson, Non-standard Analysis, Princeton, N.J., Princeton University Press, , 293 p. (ISBN 0-691-04490-2, lire en ligne)
- (en) Maxwell Rosenlicht, Introduction to Analysis, Dover, , 254 p. (ISBN 0-486-65038-3, lire en ligne) — Ce livre donne une introduction « prudente et rigoureuse » à l'analyse réelle. Il donne les axiomes des réels, puis les construit (p. 27-31) comme des développements décimaux infinis, avec 0,999… = 1 comme partie de la définition.
- (en) Walter Rudin, Principles of Mathematical Analysis, New York/St. Louis/San Francisco etc., McGraw-Hill, , 3e éd. (1re éd. 1953), 342 p. (ISBN 0-07-054235-X, lire en ligne) — Manuel pour un cours de second cycle universitaire avancé. « L'expérience m'a convaincu qu'il est pédagogiquement malavisé (bien que correct logiquement) de démarrer la construction des réels à partir des rationnels. Au début, la plupart des étudiants ne voient tout simplement pas pourquoi le faire. Donc on introduit le système des réels comme un corps ordonné satisfaisant la propriété de la borne supérieure, et on en montre rapidement quelques propriétés. Cependant la construction de Dedekind n'est pas omise. Elle est mise en appendice du chapitre 1, où elle peut être étudiée et appréciée quand le temps en est venu. » (p. ix).
- (en) Charles Smith et Charles Harrington, Arithmetic for Schools, Macmillan, (présentation en ligne)
- (en) Houshang Sohrab, Basic Real Analysis, Birkhäuser, , 559 p. (ISBN 0-8176-4211-0, lire en ligne)
- (en) Ian Stewart et David Tall, The Foundations of Mathematics, Oxford University Press, (ISBN 0-19-853165-6, lire en ligne)
- (en) Ian Stewart, Professor Stewart's Hoard of Mathematical Treasures, Profile Books, (ISBN 978-1-84668-292-6)
- (en) Ian Stewart, Calculus : Early Transcendentals, Cengage Learning, , 1344 p. (ISBN 978-0-538-49790-9, lire en ligne) — Ce livre vise à « aider les étudiants à découvrir l'analyse » et à « se concentrer sur la compréhension des concepts » (p. v). Il omet les démonstrations des fondements de l'analyse.
- (en) D. O. Tall et R. L. E. Schwarzenberger, « Conflicts in the learning of real numbers and limits », Mathematics Teaching, vol. 82, , p. 44-49 (lire en ligne)
- (en) David Tall, « Conflicts and Catastrophes in the Learning of Mathematics », Mathematical Education for Teaching, vol. 2, no 4, (lire en ligne)
- (en) David Tall, « Cognitive Development In Advanced Mathematics Using Technology », Mathematics Education Research Journal, vol. 12, no 3, , p. 210-230 (lire en ligne)
- (de) Hans von Mangoldt, Einführung in die höhere Mathematik, Leipzig, Verlag von S. Hirzel, , 1re éd., « Chap. : Reihenzahlen »
- (en) Hans de Vreught, « sci.math FAQ: Why is 0.9999… = 1? »
- (en) A. N. Walker, « Hackenstrings and the 0.999… ?= 1 FAQ », (version du sur Internet Archive)
- (en) David Foster Wallace, Everything and More : A Compact History of Infinity, New York, Norton, , 319 p. (ISBN 0-393-00338-8)
Voir aussi
[modifier | modifier le code]Liens externes
[modifier | modifier le code]- (en) « I would like to know why .9999... = 1 ? », sur mathcentral.uregina.ca
- (en) « Repeating Nines », sur descmath.com
- (en) « Point nine recurring equals one », sur qntm.org
- (en) Timothy Gowers, « What is so wrong with thinking of real numbers as infinite decimals? »,
Bibliographie
[modifier | modifier le code]- (en) Bob Burn, « 81.15 A case of conflict », The Mathematical Gazette, vol. 81, no 490, , p. 109-112 (JSTOR 3618786)
- (en) J. B. Calvert, E. R. Tuttle, Michael S. Martin et Peter Warren, « The age of Newton: an intensive interdisciplinary course », The History Teacher, vol. 14, no 2, , p. 167-190 (JSTOR 493261)
- (en) Younggi Choi et Jonghoon Do, « Equality involved in 0.999… and (-8)13 », For the Learning of Mathematics, vol. 25, no 3, , p. 13-15, 36 (JSTOR 40248503)
- (en) Tony Gardiner, « Infinite processes in elementary mathematics: how much should we tell the children ? », The Mathematical Gazette, vol. 69, no 448, , p. 77-87 (JSTOR 3616921)
- (en) Richard Mankiewicz, The Story of Mathematics, Londres, Cassell, , 192 p. (ISBN 0-304-35473-2) — Mankiewicz cherche à présenter « l'histoire des mathématiques de façon accessible » en combinant les aspects visuels et qualitatifs des mathématiques, les écrits de mathématiciens, et des ébauches historiques (p. 8).
- (en) John Monaghan, « Real mathematic: one aspect of the future of A-level », The Mathematical Gazette, vol. 72, no 462, , p. 276-281 (JSTOR 3619940)
- (en) Malgorzata Przenioslo, « Images of the limit of function formed in the course of mathematical studies at the university », Educational Studies in Mathematics, vol. 55, no 1, , p. 103-132 (DOI 10.1023/B:EDUC.0000017667.70982.05)
- (en) James T. Sandefur, « Using self-similarity to find length, area, and dimension », American Mathematical Monthly, vol. 103, no 2, , p. 107-120 (JSTOR 2975103)
- (en) Anna Sierpińska, « Humanities students and epistemological obstacles related to limits », Educational Studies in Mathematics, vol. 18, no 4, , p. 371-396 (DOI 10.1007/BF00240986, JSTOR 3482354)
- (en) Jennifer Earles Szydlik, « Mathematical beliefs and conceptual understanding of the limit of a function », Journal for Research in Mathematics Education, vol. 31, no 3, , p. 258-276 (JSTOR 749807)
- (en) David O. Tall, « Dynamic mathematics and the blending of knowledge structures in the calculus », ZDM Mathematics Education, vol. 41, no 4, , p. 481-492 (DOI 10.1007/s11858-009-0192-6)
- (en) David O. Tall, « Intuitions of infinity », Mathematics in School, , p. 30-33


 French
French Deutsch
Deutsch













![{\displaystyle \left]0,1\right[^{\ast }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbe548fb3434abeb7d5e0b870086870b31142779)




![{\displaystyle {\begin{array}{cl}0{,}\underbrace {999\ldots } &=\,1-1/10^{[\mathbb {N} ]}\\[-1ex][\mathbb {N} ]&\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/457aede52e0ff1796e1f402f6521f7cec9620c9d)
![{\displaystyle [\mathbb {N} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1054d554c515a9620eebaa21c348cd79895da027)

















