En géométrie , la formule de Bretschneider permet de calculer l'aire d'un quadrilatère non croisé :
S = ( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d cos 2 ( α + γ 2 ) {\displaystyle S={\sqrt {(p-a)(p-b)(p-c)(p-d)-abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)}}} où, a , b , c , d, sont les longueurs des côtés du quadrilatère, p le demi-périmètre, et α et γ deux angles opposés quelconques [ 1]
On peut remarquer que cos ( α + γ ) = cos ( β + δ ) {\displaystyle \cos(\alpha +\gamma )=\cos(\beta +\delta )} α + β + γ + δ = 2 π {\displaystyle \alpha +\beta +\gamma +\delta =2\pi }
Cette formule fonctionne pour un quadrilatère convexe ou concave (mais non croisé), non forcément inscriptible .
Elle généralise la formule de Brahmagupta de l'aire d'un quadrilatère inscriptible (cas α + γ = π {\displaystyle \alpha +\gamma =\pi } formule de Héron de l'aire d'un triangle (cas d = 0 {\displaystyle d=0}
Elle montre qu'un quadrilatère articulé possède une aire maximale lorsqu'on inscrit ses sommets dans un cercle.
Elle a été découverte en 1842 par le mathématicien allemand Carl Anton Bretschneider [ 2]
En la séparant par l'une des diagonales intérieures (disons [BD ]), la surface du quadrilatère est réunion de deux surfaces triangulaires. Son aire est alors donnée par
S = a d sin α 2 + b c sin γ 2 . {\displaystyle {\begin{aligned}S&={\frac {ad\sin \alpha }{2}}+{\frac {bc\sin \gamma }{2}}.\end{aligned}}} D'où
4 S 2 = ( a d ) 2 sin 2 α + ( b c ) 2 sin 2 γ + 2 a b c d sin α sin γ . {\displaystyle 4S^{2}=(ad)^{2}\sin ^{2}\alpha +(bc)^{2}\sin ^{2}\gamma +2abcd\sin \alpha \sin \gamma .} Or la formule d'Al-Kashi donne
B D 2 = a 2 + d 2 − 2 a d cos α = b 2 + c 2 − 2 b c cos γ . {\displaystyle BD^{2}=a^{2}+d^{2}-2ad\cos \alpha =b^{2}+c^{2}-2bc\cos \gamma .} Cela peut être réécrit en
( a 2 + d 2 − b 2 − c 2 ) 2 4 = ( a d ) 2 cos 2 α + ( b c ) 2 cos 2 γ − 2 a b c d cos α cos γ . {\displaystyle {\frac {(a^{2}+d^{2}-b^{2}-c^{2})^{2}}{4}}=(ad)^{2}\cos ^{2}\alpha +(bc)^{2}\cos ^{2}\gamma -2abcd\cos \alpha \cos \gamma .} En ajoutant ceci à la formule ci-dessus donnant 4 S 2 {\displaystyle 4S^{2}}
4 S 2 + ( a 2 + d 2 − b 2 − c 2 ) 2 4 = ( a d ) 2 + ( b c ) 2 − 2 a b c d cos ( α + γ ) = ( a d + b c ) 2 − 2 a b c d − 2 a b c d cos ( α + γ ) = ( a d + b c ) 2 − 4 a b c d ( cos ( α + γ ) + 1 2 ) = ( a d + b c ) 2 − 4 a b c d cos 2 ( α + γ 2 ) . {\displaystyle {\begin{aligned}4S^{2}+{\frac {(a^{2}+d^{2}-b^{2}-c^{2})^{2}}{4}}&=(ad)^{2}+(bc)^{2}-2abcd\cos(\alpha +\gamma )\\&=(ad+bc)^{2}-2abcd-2abcd\cos(\alpha +\gamma )\\&=(ad+bc)^{2}-4abcd\left({\frac {\cos(\alpha +\gamma )+1}{2}}\right)\\&=(ad+bc)^{2}-4abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right).\end{aligned}}} Après factorisation de ( a 2 + d 2 − b 2 − c 2 ) 2 − 4 ( a d + b c ) 2 {\displaystyle (a^{2}+d^{2}-b^{2}-c^{2})^{2}-4(ad+bc)^{2}}
16 S 2 = ( a + b + c − d ) ( a + b − c + d ) ( a − b + c + d ) ( − a + b + c + d ) − 16 a b c d cos 2 ( α + γ 2 ) , {\displaystyle 16S^{2}=(a+b+c-d)(a+b-c+d)(a-b+c+d)(-a+b+c+d)-16abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right),} qui s'écrit aussi
S 2 = ( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d cos 2 ( α + γ 2 ) {\displaystyle S^{2}=(p-a)(p-b)(p-c)(p-d)-abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)} d'où la formule de Bretschneider.
Voir une autre démonstration dans [ 3]
En ajoutant les aires des quatre triangles découpés par les diagonales, on obtient :
S = 1 2 e f | sin θ | = 1 2 ‖ A C → ∧ B D → ‖ {\displaystyle S={\frac {1}{2}}ef|\sin \theta |={\frac {1}{2}}\lVert {\overrightarrow {AC}}\land {\overrightarrow {BD}}\ \rVert } où e et f sont les longueurs des diagonales et θ {\displaystyle \theta }
En utilisant la formule d'Al-Kashi dans les quatre triangles découpés par les diagonales, on obtient :
2 e f cos θ = ± ( a 2 − b 2 + c 2 − d 2 ) {\displaystyle 2ef\cos \theta =\pm (a^{2}-b^{2}+c^{2}-d^{2})} D'où, d'une part :
S = 1 4 | a 2 − b 2 + c 2 − d 2 | ⋅ | tan θ | {\displaystyle S={\frac {1}{4}}|a^{2}-b^{2}+c^{2}-d^{2}|\cdot |\tan \theta |} d'autre part [ 1]
S = 1 4 4 e 2 f 2 − ( a 2 − b 2 + c 2 − d 2 ) 2 {\displaystyle S={\tfrac {1}{4}}{\sqrt {4e^{2}f^{2}-(a^{2}-b^{2}+c^{2}-d^{2})^{2}}}} Cette formule peut être modifiée en
S = ( p − a ) ( p − b ) ( p − c ) ( p − d ) − 1 4 ( a c + b d + e f ) ( a c + b d − e f ) {\displaystyle S={\sqrt {(p-a)(p-b)(p-c)(p-d)-{\tfrac {1}{4}}(ac+bd+ef)(ac+bd-ef)}}} forme due à Coolidge [ 4]
Cette forme permet aussi de retrouver la formule de Brahmagupta pour le cas inscriptible, car dans ce cas, d'après le théorème de Ptolémée , a c + b d = e f {\displaystyle ac+bd=ef}
Le fisc égyptien utilisait pour le calcul de l'aire d'un champ quadrilatéral convexe le produit des longueurs moyennes des côtés opposés : S ′ = A B + C D 2 × A C + B D 2 {\displaystyle S'={\frac {AB+CD}{2}}\times {\frac {AC+BD}{2}}} [ 5]
On a S ⩽ S ′ {\displaystyle S\leqslant S'} [ 5]
Démonstration
On a :
4 S ′ = A B ⋅ A C + B A ⋅ B D + C A ⋅ C D + D B ⋅ D C ⩾ A B ⋅ A C ⋅ sin α + B A ⋅ B D ⋅ sin β + C A ⋅ C D ⋅ sin γ + D B ⋅ D C ⋅ sin δ = 4 S {\displaystyle 4S'=AB\cdot AC+BA\cdot BD+CA\cdot CD+DB\cdot DC\geqslant AB\cdot AC\cdot \sin \alpha +BA\cdot BD\cdot \sin \beta +CA\cdot CD\cdot \sin \gamma +DB\cdot DC\cdot \sin \delta =4S} Il y a égalité si et seulement si les sinus valent 1, c'est-à-dire si le quadrilatère est un rectangle.
↑ a et b Michel Lafond, « Les formules de Bretschneider, Coolidge et Bramagupta », Feuille de vigne , octobre 2009 , p. 13-16 (lire en ligne ) ↑ (de) C.A. Bretschneider, « Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes. », Archiv der Mathematik und Physik, Band 2 1842 , p. 225-261 (lire en ligne ) ↑ E. A. José García, Two Identities and their Consequences , MATINF, 6 (2020) 5-11. ↑ (en) J.L. Coolidge, « A Historically Interesting Formula for the Area of a Quadrilateral », Amer. Math. Monthly 46 1939 , p. 345-347 (lire en ligne ) ↑ a et b Hervé Lehning, Toutes les mathématiques du monde , Flamarion, 2017 (lire en ligne ) , p. 43 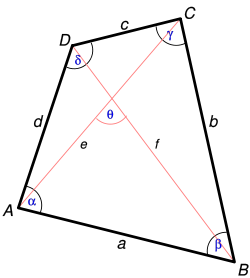



 French
French Deutsch
Deutsch






















