Équation différentielle — Wikipédia

En mathématiques, une équation différentielle est une équation dont la ou les inconnues sont des fonctions ; elle se présente sous la forme d'une relation entre ces fonctions inconnues et leurs dérivées successives. C'est un cas particulier d'équation fonctionnelle. Notons que souvent, quand on parle d'équation différentielle, on sous-entend qu'elle est ordinaire, c'est-à-dire que les fonctions inconnues ne dépendent que d'une seule variable.
Une équation différentielle permet de modéliser des situations très diverses, que ce soit en physique, en économie, en biologie, en sciences de l'ingénieur ou dans d'autres domaines encore, dans lesquelles la vitesse de variation d'une quantité a une relation déterminée à cette quantité. Seules quelques équations différentielles très simples ont des solutions exactes. Néanmoins, on peut trouver des propriétés des solutions sans les connaître explicitement, en travaillant à partir des équations différentielles elles-mêmes. Dans les cas où une solution exacte d'un système d'équations différentielles n'existe pas, on peut cependant trouver des solutions approchées par des méthodes d'approximation numérique, qui sont devenues très précises et efficaces depuis le développement de l'informatique. Sinon, avec l'aide des mathématiques pures, la théorie des systèmes dynamiques permet de connaître certaines propriétés des solutions.
Exemple tiré de la mécanique
[modifier | modifier le code]En mécanique classique, le mouvement d'un corps est décrit par sa position et sa vitesse en fonction du temps. Grâce aux lois de Newton, on peut écrire le problème comme une équation différentielle avec comme inconnue la position du solide en fonction du temps, sa vitesse et son accélération étant ses dérivées première et seconde, et les paramètres étant les différentes forces agissant sur ce corps. Dans certains cas simples ou après des simplifications du problème, l'équation différentielle, appelée équation du mouvement, peut être résolue de façon explicite.
Un exemple de la vie courante faisant appel à l'équation du mouvement est la détermination de la vitesse d'une balle tombant en l'air, et subissant comme forces uniquement la loi de la gravité et la résistance de l'air, toutes deux étant exercées verticalement, et la seconde limitant la première. La gravité est constante, et la résistance de l'air peut être modélisée simplement en la considérant comme proportionnelle à la vitesse :
où :
- désigne la gravité exercée sur la balle ;
- désigne la résistance de l'air qu'elle subit ;
- est sa masse inertielle (qui se révèle égale à la masse gravitationnelle, voir principe d'équivalence) ;
- est la vitesse de son centre d'inertie G ;
- est le temps.
Pour résoudre cette équation différentielle ordinaire, on peut poser l'hypothèse simplificatrice suivante :
- , où est une constante réelle positive, et , une fonction du temps .
On obtient alors l'équation différentielle , qui, en se projetant sur l'axe vertical, direction du mouvement de la balle, se réécrit :
, et qui est une équation différentielle linéaire d'ordre un, linéaire car les coefficients de et de sa dérivée sont constants, et d'ordre un, car la dérivée d'ordre le plus élevé est la dérivée première .
La solution de cette équation différentielle est : .
Histoire des équations différentielles
[modifier | modifier le code]Des modélisations mathématiques étaient déjà en cours de développement à l'époque de la Renaissance. Mais l'utilisation explicite des équations différentielles formelles apparaît avec l'invention du calcul infinitésimal par Isaac Newton et Gottfried Leibniz. Newton en définit trois dans son traité de Methodis Serierum et Fluxionum[1] : , où est la fonction inconnue, dépendant de (ou de et si c'est une fonction de plusieurs variables), et où est une fonction donnée. Il résout ces exemples en faisant appel aux séries infinies, et étudie la possibilité de plusieurs solutions.
Jacques Bernoulli proposa une autre forme d'équation différentielle en 1695:
Leibniz réussit à en trouver des solutions quelques années plus tard, en la simplifiant.
L'une des premières questions de physique à nécessiter l'appel aux équations différentielles fut le problème d'une corde vibrante, comme pour un instrument de musique. Ce problème fut étudié par Jean le Rond d'Alembert, Leonhard Euler, Daniel Bernoulli, et Joseph-Louis Lagrange[2],[3]. En 1746, d'Alembert découvrit l'équation d'une onde en une dimension, et quelques années plus tard, Euler découvrit l'équation d'une onde en trois dimensions[4].
L'équation d'Euler-Lagrange fut développée dans les années 1750 par les deux mathématiciens pour résoudre en particulier le problème des courbes tautochrones. Lagrange résolut le problème en 1755, et envoya la solution à Euler. Tous deux développèrent à partir de cela la méthode de Lagrange et l'appliquèrent à la mécanique, ce qui aboutit à la formulation de la mécanique lagrangienne.
En 1822, Joseph Fourier publia son travail sur le transfert thermique, dans son traité Théorie analytique de la chaleur[5], dans le quel il s'appuie sur la loi de refroidissement de Newton. Dans son traité, il établit une équation de la chaleur, une équation aux dérivées partielles, qui décrit le phénomène physique de conduction thermique. Cette équation a été utilisée depuis dans de nombreux autres domaines des mathématiques et de la physique (théorie des probabilités, mathématiques financières, mécanique quantique,...).
Types d'équations différentielles
[modifier | modifier le code]Les équations différentielles peuvent être caractérisées de plusieurs manières. Cette caractérisation aide à trouver les bons outils convenant à chaque équation différentielle pour trouver des solutions ou du moins en découvrir des propriétés. La caractérisation la plus importante est la distinction entre les équations différentielles ordinaires (EDO) et les équations aux dérivées partielles, où la ou les fonctions inconnues recherchées peuvent dépendre de plusieurs variables indépendantes (EDP). On peut aussi distinguer les équations différentielles linéaires et non linéaires, et les équations différentielles homogènes, ou non homogènes.
Il existe aussi d'autres types particuliers d'équations différentielles : les équations intégro-différentielles (IDE), qui contiennent à la fois des dérivées et des primitives des solutions ; les équations différentielles raides, dont les solutions sont sensibles aux variations des paramètres ; les équations différentielles holomorphes (EDH) où la ou les fonctions inconnues dépendent d'une seule variable complexe ; les équations différentielles stochastiques (EDS) où un ou plusieurs paramètres de l'équation différentielle sont des processus stochastiques ; les équations différentielles à retard (EDR) dans lesquelles la dérivée de la fonction inconnue à un moment donné est exprimée selon les valeurs de la fonction aux temps précédents ; les équations différentielles abstraites (EDA) où les fonctions inconnues et leurs dérivées prennent leurs valeurs dans des espaces fonctionnels abstraits (espace de Hilbert, espace de Banach, etc.).
Existence de solutions
[modifier | modifier le code]La résolution d'une équation différentielle est nettement plus complexe que celle d'une équation algébrique pour plusieurs raisons. D'abord, on ne peut pas savoir a priori s'il existe une ou plusieurs solutions, ou aucune. De plus, la solution peut rarement être exprimée de façon explicite.
Pour les équations différentielles du premier ordre ayant certaines conditions initiales, le théorème de Cauchy-Peano-Arzelà donne un ensemble de conditions pour qu'une solution existe. Soit un point dans le plan, définissant une région rectangulaire , telle que et est à l'intérieur de . Pour une équation différentielle donnée avec la condition que quand , alors il existe une solution locale du problème si et sont toutes deux continues sur . Cette solution est définie sur un certain intervalle autour de . Il peut y avoir plusieurs solutions. Ce théorème n'est valable que pour des équations différentielles du premier ordre, avec des conditions aux limites définies.
Pour un problème du nième ordre
avec des conditions initiales telles que
- ,
alors, pour toute fonction non nulle , si et sont continues sur un certain intervalle contenant , existe et est unique[6].
Exemples d'équations différentielles
[modifier | modifier le code]Équations du premier ordre
[modifier | modifier le code]- Équation différentielle linéaire à variables séparables
Les équations différentielles les plus simples sont les équations linéaires homogènes du premier ordre. Par exemple, équation différentielle linéaire à variables séparables, de la forme :
où f est une fonction connue admettant des primitives. Une façon directe de la résoudre est de considérer, pour f(t) non nul, la forme avec les variables séparées :
Par intégration, il vient alors :
où A = eC est une constante arbitraire.
- Équation différentielle linéaire à variables non séparables
Le cas plus général inclut des formes où les variables ne sont pas séparables, comme :
où p et q sont des fonctions connues admettant des primitives. Une façon directe de la résoudre est de la réécrire avec un facteur intégrant :
Ce qui donne, en remultipliant par le facteur μ
dont on déduit la forme générale de la solution :
Équations du second ordre
[modifier | modifier le code]- Oscillation simple non amortie
Les mouvements périodiques dont on néglige les effets de frottement qui vont le ralentir (comme l'allongement du ressort x(t) à un temps t) peuvent être modélisés par l'équation différentielle suivante :
- où ω est un réel positif
Dont les solutions sont :
Pour déterminer les constantes A et B, il faut utiliser les conditions initiales qui permettent de décrire l'état du système à un instant donné (correspondant en général à t = 0).
Par exemple si on suppose qu'à l'instant t = 0, l'extension du ressort est d'une unité de longueur (x = 1), et la masse est immobile (dx/dt = 0). On peut en déduire
- ,
d'où l'on déduit A = 1.
- ,
et donc B = 0.
En conséquence est solution de l'équation différentielle étudiée.
Plus souvent en physique pour les oscillations simples non amorties, on utilise une solution de la forme :
avec A étant l'amplitude et ϕ la phase.
Pour l'exemple cité on procède :
Ce qui donne ϕ = 0 et par conséquent A = 1.
D'où le résultat
La solution la plus générale en fonction de conditions initiales quelconques x0 et est donnée par l'équation :
- Prise en compte de l'amortissement
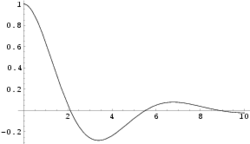
Le modèle précédent négligeait les forces de frottement. De ce fait l'oscillation libre pouvait durer indéfiniment, ce qui n'est jamais observé en réalité.
Les frottements sont en général une force proportionnelle à la vitesse (dx/dt) et opposée au mouvement. En rajoutant ce terme notre équation différentielle devient :
- où c > 0 est le coefficient de frottement.
Ceci est une équation différentielle linéaire à coefficients constants, homogène et du second ordre, qu'on peut résoudre.
En cherchant une solution de la forme particulière A ekt, on constate que k doit vérifier l'équation caractéristique suivante :
- .
On revient ainsi à l'étude d'une équation du second degré. Si c < 2ω, on a deux racines complexes conjuguées (de la forme a ± i b), et la solution (avec les conditions initiales identiques au cas précédent) a la forme suivante :
On peut démontrer que a < 0.
Le système étudié (le pendule pesant dans le référentiel terrestre supposé galiléen) est le siège d'oscillations libres amorties.
Ce sont les positions du centre d'inertie de la masse, en fonction du temps, avec x = 0 correspondant à une position d'équilibre.
NB : la courbe présente une allure proche d'un régime critique : la position d'équilibre est à peine franchie, et on ne compte guère plus d'une pseudo-période d'oscillations.
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]- Cet article est partiellement ou en totalité issu de l'article intitulé « Exemples d'équations différentielles » (voir la liste des auteurs).
Références
[modifier | modifier le code]- ↑ Newton, Isaac. (c.1671). Methodus Fluxionum et Serierum Infinitarum (The Method of Fluxions and Infinite Series), published in 1736 [Opuscula, 1744, Vol. I. p. 66].
- ↑ Craig Frasier, « Review of The evolution of dynamics, vibration theory from 1687 to 1742, by John T. Cannon and Sigalia Dostrovsky », Bulletin of the American Mathematical Society, vol. 9, no 1, (lire en ligne)
- ↑ Gerard F. Wheeler et William P. Crummett, « The Vibrating String Controversy », Am. J. Phys., vol. 55, no 1, , p. 33–37 (DOI 10.1119/1.15311, Bibcode 1987AmJPh..55...33W)
- ↑ Speiser, David. Discovering the Principles of Mechanics 1600-1800, p. 191 (Basel: Birkhäuser, 2008).
- ↑ Joseph Fourier, Théorie analytique de la chaleur, Paris, Firmin Didot Père et Fils, (OCLC 2688081, lire en ligne)
- ↑ Dennis G. Zill, A First Course in Differential Equations, Brooks/Cole, , 5th éd. (ISBN 0-534-37388-7)
Voir aussi
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]- (en) Carl B. Boyer, The Concepts of the Calculus: A Critical and Historical Discussion of the Derivative and the Integral, Hafner Publishing Company, ; republication : (en) Carl B. Boyer, The History of the Calculus and Its Conceptual Development, Dover, (lire en ligne).
- (en) Dirk Jan Struik (ed.), A Source Book in Mathematics, 1200-1800, Cambridge, MA, Harvard University Press, (lire en ligne), p. 238-243; 271-281.
- (en) Florian Cajori, « The History of Notations of the Calculus », Annals of Mathematics, vol. 25, no 1, , p. 1-46 (lire en ligne).
Articles connexes
[modifier | modifier le code]- équation différentielle ordinaire
- équation aux dérivées partielles
- équation différentielle linéaire
- équations de Navier-Stokes
- méthode d'Euler
- méthode des différences finies
- méthode des éléments finis
- méthode des volumes finis
- Intégration
- Analyse vectorielle


 French
French Deutsch
Deutsch






















![{\displaystyle Z=[l,m]\times [n,p]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/515b71ad3b5fc01ff532df8cb71018baca811973)
































